- 近期网站停站换新具体说明
- 按以上说明时间,延期一周至网站时间26-27左右。具体实施前两天会在此提前通知具体实施时间
主题:【原创】化工过程控制的实践 -- 润树
MPC在十几年前开始红火起来,现在也还没有衰竭的迹象。从技术上来说,我想可能有两个重要的因素在起作用。一是其模型预估的功能,使一些比较难于控制的变量能够得到较好的控制,二是过程模型的建立使得多变量控制变得比较容易实现。其结果,当然必须在改善过程的生产效益,减少能源消耗,提高产能上体现出来。下面,我们就这两个因数具体地谈一谈。
为什么模型预估能够改善控制效果呢?这要从常规PID(比值加积分加微分)控制谈起。如图3.0.1所示的常规PID控制回路方框图,PID的输入e,是我们所希望过程要达到的设定点SP与过程实际输出值y之间的差值,我们把它叫作偏差。当这个偏差稳定在零或很小的数值时,过程就算达到了稳态。一但设定点改变,或过程受到干扰而其输出发生变化,偏差就不再是零,控制器就会通过PID的算法,来改变控制器输出即过程的输入u,来把偏差重新驱动到零。
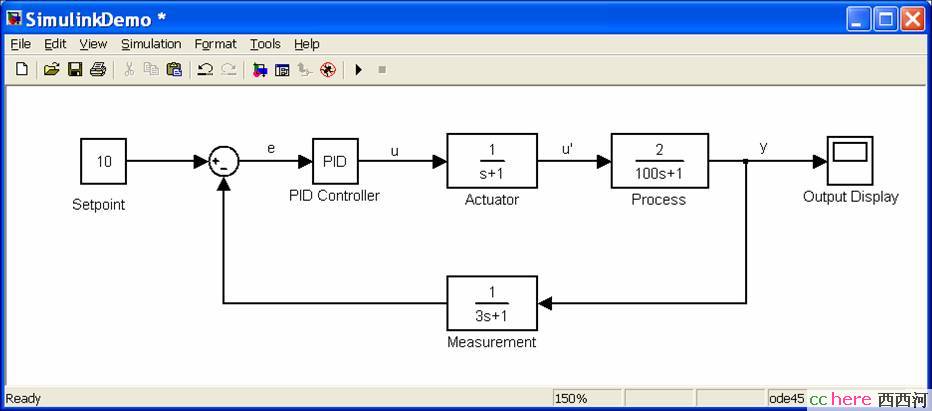
图3.0.1 典型的控制系统方框图
问题是,究竟过程的输入应该是多少才能使其输出达到设定值,从而使偏差为零呢?PID控制器并不确切地知道,它所知道的是,如果偏差为正值,那么我应该大概增加多少过程输入(这里的过程增益为正),而如果偏差为负值,我就应该大概减少多少过程的输入。这里大概增加多少/大概减少多少的数值,取决于工程师根据对过程的认识来设定的PID参数。因此,参数设定得好,控制系统就能很快消除偏差;反之,则可能要经过很长的时间才能消除偏差(图3.0.2a),严重时偏差将在正负值之间来回振荡,导致系统长时间不能稳定下来(图3.0.2b)。
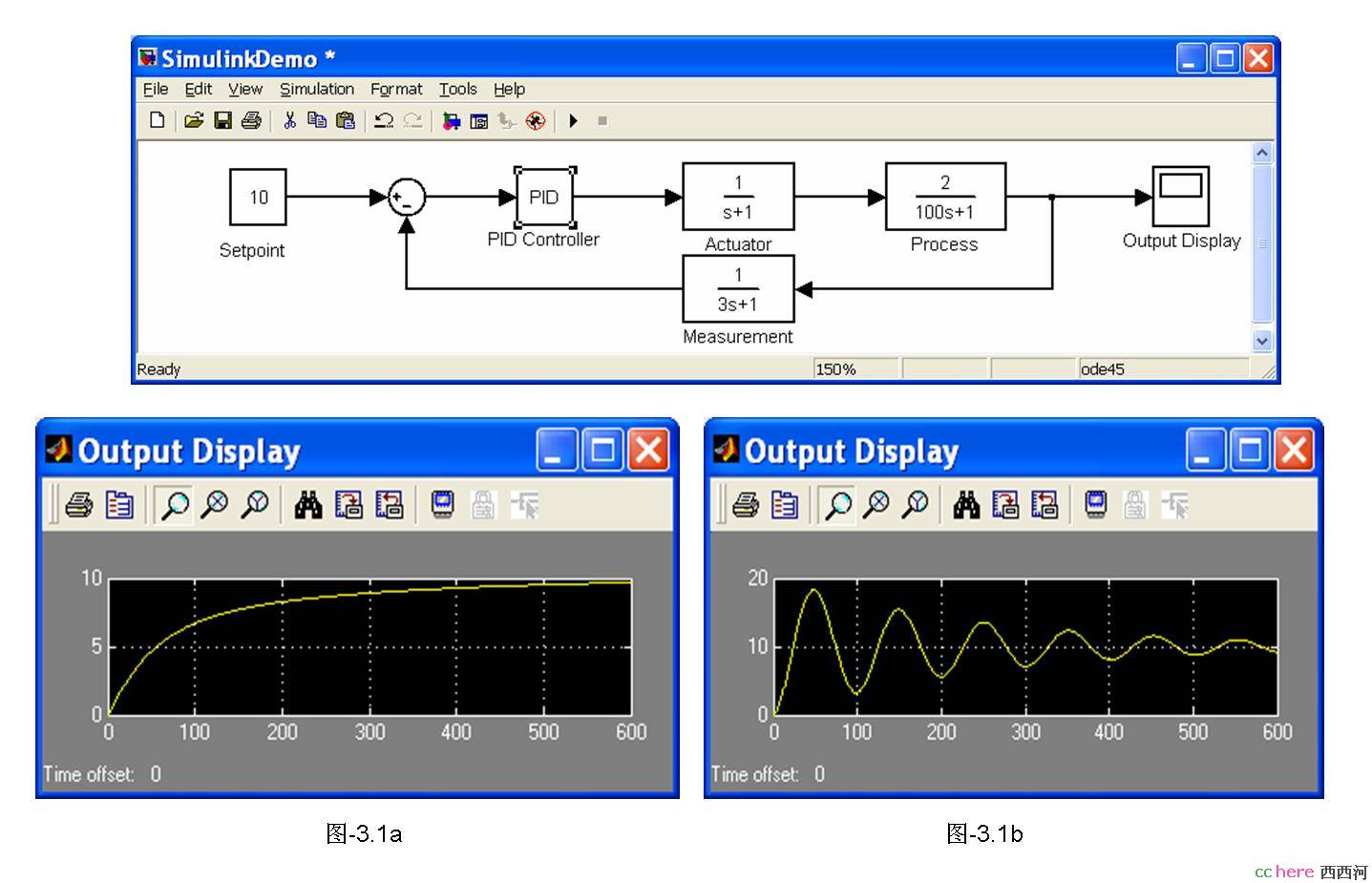
图3.0.2 不同参数设定下的PID控制响响应
显然,这里的关键是要知道过程的特性,即它的静态增益和动态时间常数(对于大多数的化工过程而言)。事实上,如果知道了该特性,那么一个理想的控制器算法不是PID,而是该过程函数的颠倒(inverse)。一个负反馈系统理想的算法,就静态来说,过程的增益和控制器的增益之乘积应该是1(即它们互为倒数);而就动态来说,过程是滞后的,那么控制器就应该是超前的。比如,一个用阀门开度来控制流量的过程函数是2 /(100S + 1),那么理想控制器应是(100S + 1)/ 2 = 50S + 0.5。也就是说,如果实际流量比设定值小2个单位,那么阀门开度应该增加1个百分度。现在我们用MATLAB仿真来看看这样的理想控制。由于是理想模型控制,我们甚至连反馈也不需要了。用Simulink的传递函数模块不能直接实现(50S + 0.5),但我们可以合理地用(50S + 0.5)/(S + 1)来近似。图3.0.3上方的两个显示分别是过程的输入和输出。我们可以看到,过程输出响应很快,几乎在瞬间就达到了设定点 (否则为什么叫理想?)。下方的两个显示是在缩短到前十几秒来看的输入和输出。
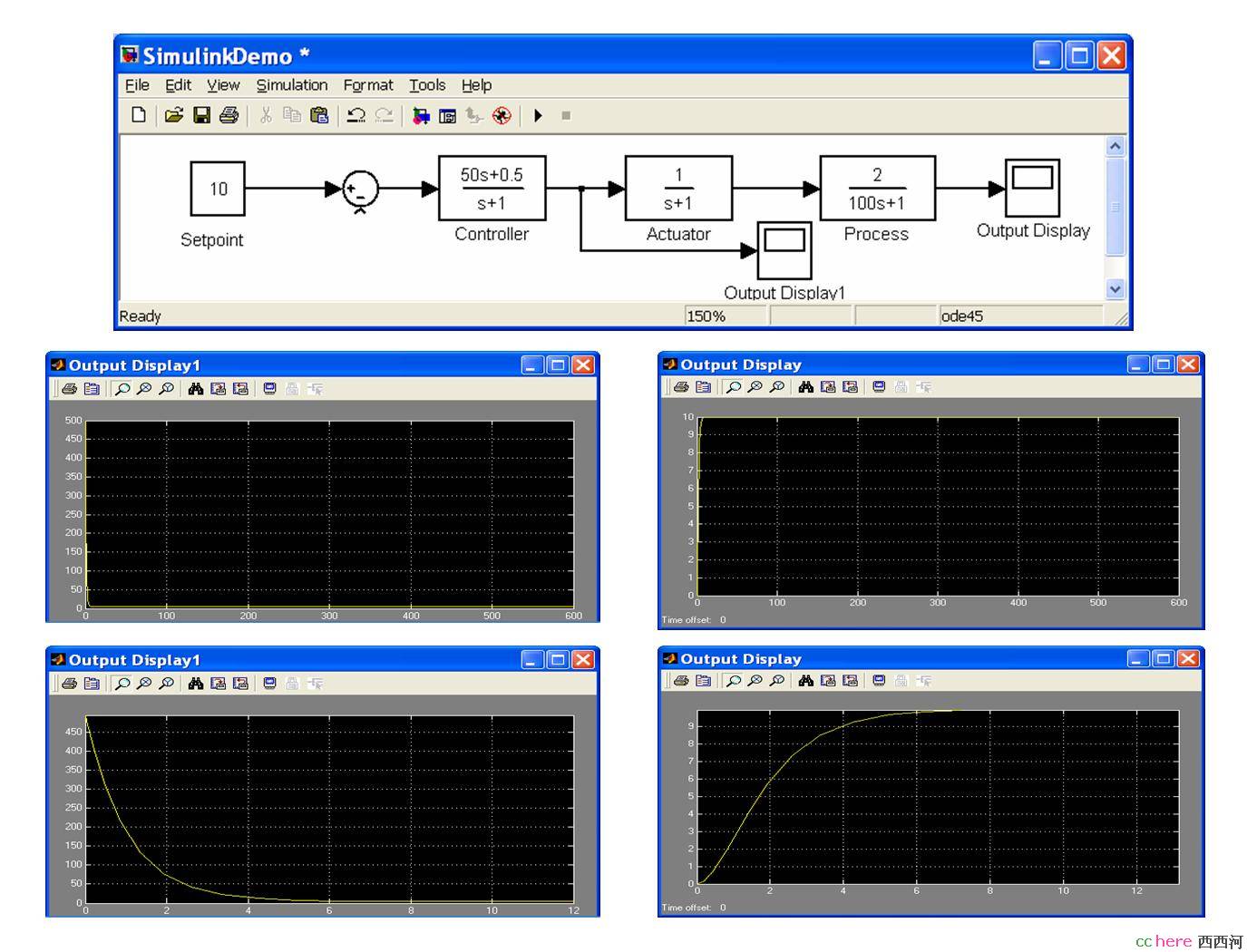
图3.0.3 理想模型控制的响应
当然在实践中,这样的理想控制是不大可能实现的,有两个原因:
1)从上例可以看到,由于控制器算法是一个很强的微分,它在设定点改变瞬间(零时刻)的输出是500,也就是说要阀门的开度达到500%,这显然是不现实的 (最大开度是100%)。也就是说,在实现模型控制时,必须考虑系统的约束条件。
2)无论用什么方法去获得过程的模型,这个模型不可能与过程实际特性完全一致。如果让系统处于开环状态,那么不但不能获得理想的控制效果,甚至连设定值都永远无法达到(没有PID的积分作用)。由于这个原因,模型控制仍然必须有反馈的机制,形成闭环控制。
在考虑以上两点的基础上,利用过程模型来预先计算(预估)过程输入输出在某一时段里的变化轨迹,从而对控制系统进行动态优化的MPC的三个基本方程就出来了:
问题: ( 1 ) Minimize Sum (e[i]’Q e[i] + u[i]’R u[i]) ,e[i] = x[i] - sp
满足: ( 2 ) x[i+1] = A x[i] + B R u[i], x[0] = x0
结果: ( 3 ) u”[i] = K[i]x”[i], i = 1, 2, …… , p
方程(1)中的e[i]’是过程偏差向量e[i]的转置,u[i]’是过程输入向量u[i]的转置,x[i]是过程的状态向量。这个方程提出的问题是,对过程的偏差向量加权的平方以及过程的输入向量加权(Q, R)的平方之和进行最小化。传统上,动态优化控制只考虑控制偏差e的轨迹,而这里输入u的的变化轨迹也成为了一个优化变量,这是因为,u的变化不但要受到物理条件(比如阀门开度不能大于100%)和安全生产(比如压缩机速度不能变化太快)的约束,而且它们的变化本身与生产成本有很大关系。在化工生产中,很大一部份的u都与能源的使用有关(裂解炉的燃料,精馏塔再沸器的蒸汽等等)。
方程(2)是用状态空间函数来描述的过程动态和静态特性。不同的MPC产品,也可能用不同的数学形式来描述此特性。
方程(3)中的u”[i]和x”[i]是求解方程(1)所获得的过程优化输入输出变量值。K[i]是在求解方程 (1) 所对应的黎卡的(Ricatti)方程所获得的状态反馈增益矩阵。
在实际的MPC计算中,还必须加入输入和输出的约束条件(通常用不等式来表达),以及从过程的实时检测来校正过程模型误差,因此比这里的三个方程要复杂得多。如果再应用到多输入多输出的控制系统中,其计算量更是庞大。我们在这里就不深入讨论了。对MPC的理论和计算有进一步兴趣的朋友,可以参考其它文献。这里向你推荐下面这篇论文。
[URL]http://www.chee.uh.edu/faculty/nikolaou/MPCtheoryRevised.pdf [/URL]
使MPC热门的第二个因素是它在多变量过程控制中的应用。传统的过程控制系统是单输入单输出(SISO)的,这对于一些简单的控制回路,像流量,压力,温度等,是很有效的,完全没有必要用MPC。但是如果要通过控制来提高某个生产装置的生产效率,就必须有一个大的控制器来对各SISO系统进行整体的协调,这就诞生了多变量的MPC。事实上,现在工业界说到MPC,都是指多变量的模型预估控制。
在此控制器中,可能有M个控制变量(manipulated variables, MV),N个被控变量(controlled variables, CV)。取决于实际的应用对象,将可能出现下面三种情形:
1)M > N,有无数个解,所有的CV都可被控制在设定值上。
2)M = N,有唯一解,所有的CV都可被控制在设定值上。
3)M < N,无解,不能将所有的CV都控制在设定值上。
由于实际应用中有众多的约束条件,以上3)是最常见的。在这样的情况下,多数CV都是被控制在某一范围之内,而不是在某一个设定值上。
MPC的输出,一般都不是直接送到生产管线上的执行单元,像阀门,电机等,而是作为SISO控制回路的设定值。这就形成了两个级别的控制系统。第一级是常规控制,大约每秒钟计算一次控制器的输出;而MPC是第二级控制,大约每分钟进行一次这样的计算。比如一个精馏塔,在常规控制下,它的塔顶回流是由一个流量调节器控制的,它的再沸器蒸汽流量是由塔底温度调节器控制的,但是这两个调节器的设定点(希望的回流量和温度值)则是由操作工手动设定的。而在MPC控制下,这两个设定点就可能成了MV,MPC通过调节它们的数值来控制塔顶和塔底产品的成分指标,形成一个2 x 2的MPC。当一个MPC所覆盖的过程很大很复杂时,它可能会有十几个甚至几十个MV和CV。
MPC在提高化工生产过程的效率上,主要着眼于以下几个方面:
1)提高原料转换成产品的转换率。这即可能体现在反应器的转换率上,也可以体现在把反应出来的产品尽可能多地从副产品中分离出来的过程中。MPC通常是通过提高过程的稳定性以及卡边操作(将某些CV推向低限或高限)等手段来达成的。
2)提高产能。一个生产装置在设计并投入运行以后,生产者一般都会通过改善操作条件来获得更高的产能,但往往会受到某些约束条件或瓶颈的限制。MPC可以将这些约束条件推倒极限,因而使装置总是处于最大产能的操作状态。
3)降低能源消耗。除了一些卡边操作的手段外,MPC的动态优化控制在这方面具有先天性的优势。
我们将在下一节讲到MPC的软件及其应用时,就MPC在提高化工生产过程的效率上举例作详细的说明。
