- 近期网站停站换新具体说明
- 按以上说明时间,延期一周至网站时间26-27左右。具体实施前两天会在此提前通知具体实施时间
主题:【翻译】计算机几何基础算法(一) -- 东方射日
多边形的面积
另外有一个普遍的问题是计算一个给出各个顶点的多边形的面积。我们考虑如下图所示的有五个顶点的非凸多边形。要计算它的面积,我们可以将它分割为一个个三角形。在这个五边形中,我们可以分割为三个三角形:ABC,ACD和ADE。不过,等等....你可能会反对,并不是每个三角形都是这个五边形的一部分。这里,叉积是有正负的优势就大大体现出来了,它会让每件事情都变得很奇妙。首先,我们计算ABxBC可以得到三角形ABC的面积,如果你还记得右手法则的话,在本例中,AB到BC是顺时针,那么我们就会得到一个负值。同样地,由ACxAD的叉积我们可以得到三角形ACD的面积,这也是一个负值。最后,我们计算ADxAE,由于ADE三点是逆时针方向,我们知道那将得到一个正值。我们将这三个面积(两负一正)相加,本例中,我们就得到一个负值,那个绝对值就是这个多边形的面积。
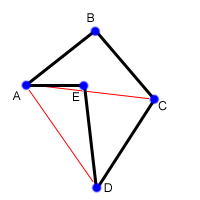
看上图,很显然多边形的面积就是三角形ABC和ACD的面积之和减去三角形ADE的面积。
最后一点提示,如果我们计算的面积是负值,表示各个顶点是按顺时针方向给出的。
下面给一段具体的代码,其中顶点是以2维数组的方式给出:
int area = 0;
int N = lengthof(p);
//We will triangulate the polygon
//into triangles with points p[0],p[i],p[i+1]
for(int i = 1; i+1<N; i++){
int x1 = p[i][0] - p[0][0];
int y1 = p[i][1] - p[0][1];
int x2 = p[i+1][0] - p[0][0];
int y2 = p[i+1][1] - p[0][1];
int cross = x1*y2 - x2*y1;
area += cross;
}
return abs(cross/2.0);
注意,如果各顶点都是整数,最后的面积是一个整数的一半。(0.5的整数倍)
线-线交点
你将发现寻找两条线的交点是最普遍的几何问题之一。尽管这个问题很普遍且看起来很简单,但是还是有许多程序员感到无从下手。第一个问题是直线是以什么形式给出的?或者说你希望它是什么形式?理想情况下,每条线都可以写成Ax+By=C的形式。ABC这三个值就可以唯一确定一条直线。然而,经常给我们的直线并不是这样的形式,不过我们总可以很容易地将两个点装换成这种标准形式。例如给出直线上两个点(x1,y1)和(x2,y2),我们可以等到相应的A,B和C:
A = y2-y1
B = x1-x2
C = A*x1+B*y1
无论直线是如何描述的,我们总可以有直线上的至少两个点,然后以上述方式得到A,B和C。好现在我们可以假定我们有两条直线:
A1x + B1y = C1 (一)
A2x + B2y = C2 (二)
那么要找这两条直线的交点就变成一个简单的二元一次方程问题。
double det = A1*B2 - A2*B1
if(det == 0){
//Lines are parallel
}else{
double x = (B2*C1 - B1*C2)/det
double y = (A1*C2 - A2*C1)/det
}
复习一下初中数学,将(一)两边乘以B2,(二)两边乘以B1,然后将两式相减得到:
A1B2x - A2B1x = B2C1 - B1C2
那么就得到 x = (B2C1 - B1C2 )/(A1B2 – A2B1) 类似第你可以得到y.
现在你就得到了两条直线的交点。那么在两条线段的情况下又怎样呢?你需要确认我们的到的点在两条线段上。如果线段的两个端点是(x1,y1)和(x2,y2),那么你只要检查min(x1,x2) ≤ x ≤ max(x1,x2) 和min(y1,y2) ≤ y ≤ max(y1,y2)就可以认为该点在线段上。这里特别提醒一下浮点数的精度问题。如果交点正好在线段的端点或线段是水平/垂直的,简单的比较是可能有问题的。这里你可以定义一个最小的许可误差或是用一个分数的类来进行。
三点确定一个圆
给出不共线的三个点就可以唯一确定一个圆。但这个圆的圆心和半径是多少呢?这个问题实际上就是求直线交点的一个简单应用。如下图示,我们首先确定XY和YZ的中垂线,他们的交点就是圆心。
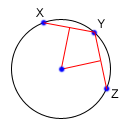
要得到XY的中垂线,首先我们可以有上面的介绍得到XY的直线Ax+By=C。那么它的中垂线就是 -Bx+Ay=D。至于D是多少,可以代入XY的中点得到。中点简单的就是XY两点的x和y坐标的平均值。同样,我们可以得到YZ的中垂线。再用上面介绍的方法得到交点,那就是圆心。
镜像
找到一个点关于一条直线的镜像,我们可以采用上面三点确定一个圆同样的技巧。首先注意到点X和镜像点X'到直线的距离相等,同时注意到XX'垂直于所给的直线。那么如果所给出的直线是Ax+By=C,我们已经知道它的垂线是-Bx+Ay=D。代入点X,就可以计算出D。现在我们可以计算这两直线的交点Y。那么X'=Y-(X-Y)
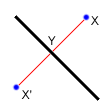
旋转
旋转并不完全和计算直线的交点相关。但是我觉得把它和镜像问题放在一起还是有好处的。事实上找到镜像点的另一种方法是将点X相对点Y旋转180度。
想象一下将一点相对另一点逆时针旋转角度θ 。简单话我们可以假设相对原点旋转,我们有x' = x Cos(θ) - y Sin(θ) 和 y' = x Sin(θ) + y Cos(θ) 。如果相对其他点旋转,那么只要将坐标平移使该点为原点,然后采用以上公式计算,接着再将坐标平移回去即可。
本帖一共被 2 帖 引用 (帖内工具实现)
- 相关回复 上下关系8
🙂【翻译】计算机几何基础算法(一) 24 东方射日 字5754 2009-01-11 21:00:16
🙂Ibackstrom是哪位 我踏月色而来 字0 2009-01-17 22:30:20
🙂我也不认识 东方射日 字154 2009-01-19 01:27:27
🙂【翻译】计算机几何基础算法(二)

🙂这一炮是白打了…… 响马 字127 2009-01-15 07:14:20
🙂科普技术贴阿,送花 木秀于林 字0 2009-01-13 03:34:54
🙂【翻译】计算机几何基础算法(三) 13 东方射日 字5277 2009-01-11 21:09:27
🙂不知你是否考虑到计算精度的问题 奔波儿 字230 2009-01-18 16:21:27