- 近期网站停站换新具体说明
- 按以上说明时间,延期一周至网站时间26-27左右。具体实施前两天会在此提前通知具体实施时间
主题:“魔改”《白蛇传》 -- 给我打钱87405
“幂势既同,则积不容异”,这就是祖暅原理。其中,幂指的横截(面),势指的是(立体的)高,祖暅原理的意思就是说若两个立体同高,又在等高处的横截面相等,那么这两个立体的体积相等。
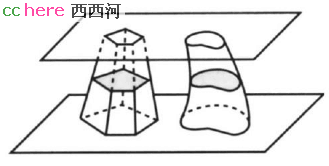
祖暅原理无法证明,然而它是对的,可是习惯了证明的人对此抱有疑虑的,所以祖暅原理到底是怎么得出的,为什么其它人想不到这才是真正需要思考的问题。
我也无法确认祖暅原理的是怎么得出的,但做为一名事后诸葛亮我认为事情是这样的:两个完全一样的立体,等高处的横截面是不是相等?
“啊!这么简单?”
要不然呢?
“不是,天呐,这太难以置信了。”
嗯,因为你不是祖暅。但你现在已经知道了祖暅原理,所以你为什么不换一个角度来想:是不是我们对于体积、面积、长度的认知出现了BUG?
不如来看下面这张图:
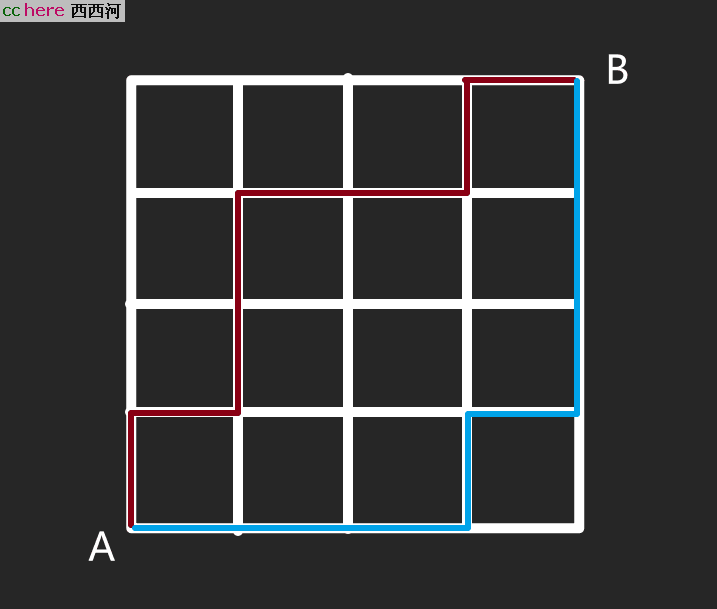
欲从A点走到B点,不论你选择哪条路径,只要你是左右交替变向,总步数总是8步,对吧?所以这又该如何解释呢?
我时常见到别人是这么生动的讲解祖暅原理的:一摞硬币叠放在一起,可不管你怎么“扭曲”,这摞硬币所占的空间大小是不会变的。

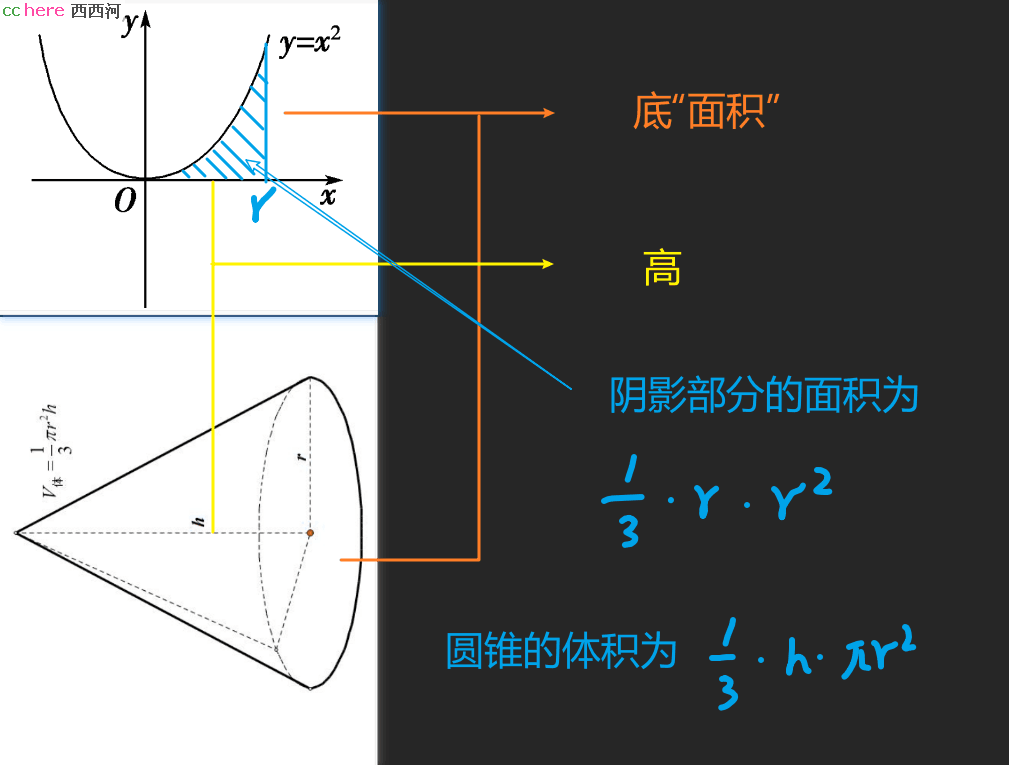
生动固然生动,但这不是祖暅原理,而是微积分。微积分才是把立体视为一个又一个的微小立体叠加在一起,祖暅原理说的是横截面相等。所以为啥圆锥的体积是(1/3)h*π*r^2?为啥棱锥的体积也是(1/3)h*S,(S为棱锥底面积)?
棱锥的体积很好求,如下:
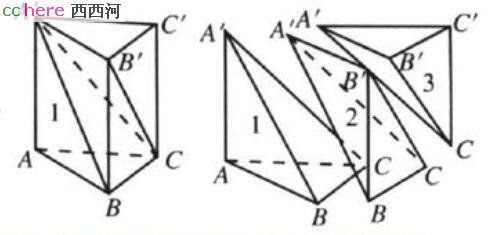
将棱柱一分为三,这三部分的体积是一样大的,而棱柱的体积为h*S。
有人告诉你,求圆锥之体积的需要用到帕普斯-古尔丁定理。帕普斯是一个古希腊人,古尔丁是另一个生活在16世纪的人,帕普斯-古尔丁定理说的是:一个平面图形绕其所在平面内的一条固定轴旋转一周所形成的立体体积等于该平面图形的面积乘以该图形重心所走过的路程。因此,依帕普斯-古尔丁定理来看,圆锥就是一个直角三角形绕其中一条直边线旋转一周而得,直角三角形的面积为rh/2;直角三角形的重心到顶点与到边的长度比为2:1,重心所走过的路程为2πr/3,圆锥的体积为(1/3)h*π*r^2。
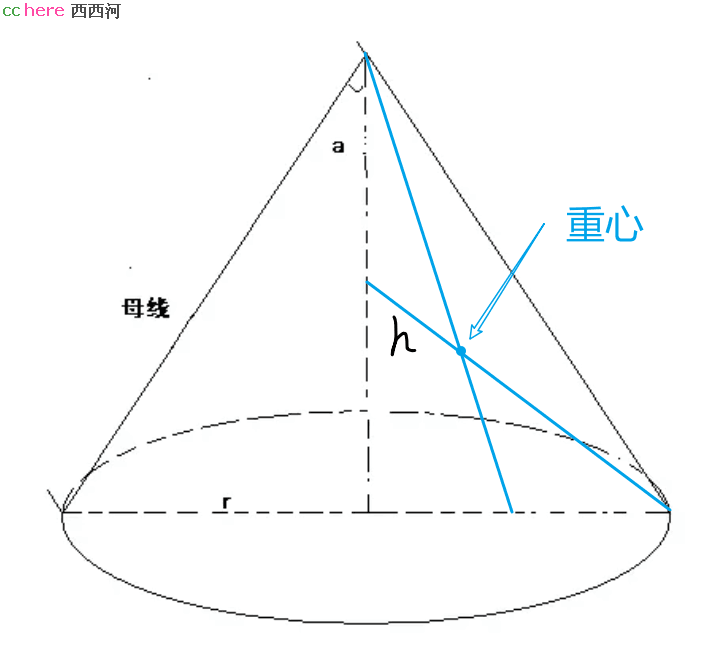
可是,这个帕普斯-古尔丁定理是怎么来的呢?等你去把资料一查你就会发现,第一、它是先有结论后有定理,换言之,是先有了体积公式后有这个定理;第二、据称,这一定理在古希腊时就被帕普斯所发现,然而后来的人忘了,直到16世纪才被重新想起来。
“啊这……”
所以凭啥说圆锥的体积是(1/3)h*π*r^2?这个1/3有没有可能是一个类似于π的数值?
“不是,根据祖暅原理,等高的圆锥体和棱锥的体积是相等的啊!”
可是祖暅原理无法证明啊。
“不是,根据微积分原理,等高的圆锥体之体积跟棱锥是同构的啊!”
可是微积分思想是错的,曲的就是曲的,无论如何细分。
祖暅原理无法证明,微积分思想是错的,然而双方得出的结论(数值)是相等的,是不是很有趣?
“你在暗示什么吗?”
我不暗示,我要么用明语,要么发密码,我的话就已经说得很清楚了,祖暅原理无法证明,这是西方人坚持要证明;微积分思想是错的,然而用微积分公式却能推出一模一样的结论,所以很显然,是西方人抄袭了别人的成果,然后又倒转过来胡解释了一番。
祖暅原理是祖暅提出的,别人不知道他是如何做到的,所以你可以不信,因为无法证明。
很有可能,我们对长度、面积、体积的认知出了BUG。我们只是知道如何求出【规则图形】的长度、面积、体积,最基础的方法就是【度】,用“1”来度量其它的长度,再进一步度出面积,再进一步度出体积。可是,什么是长度、面积、体积,我们知道答案吗?
我有理由相信,祖暅触摸到了“天机”,这个理由就是根据祖暅原理可以“跨界”操作,用一个已知的立体之体积来求得一个未知的平面之面积。
还有一个有趣的问题:正方形的内接圆半径为r,则有:
正方形的面积为4r^2,内接圆的面积为πr^2;
正方形的周长为8r,内接圆的周长为2πr。
所以为啥这两组的比值都是4:π?
经常有人说我是上知天文下晓地理,我说并不是,有许多问题我根本就不知道如何去回答,但对方往往说我过于谦虚,再这么谦虚下去就显得虚伪了,你看我是虚伪吗?我不知道什么是空间,所以我无法回答出“宇宙有多大”这个问题,如果宇宙有大小,那么就意味着宇宙的外面还有什么,有限的宇宙被装在这什么里面故而能测出其大小,这样一来,宇宙就不是宇宙了,因为宇宙的定义就是一切;我也不知道什么是时间,对于人类而言,时间的定义就是哪天人类挂了时间也就不存在了。
你知道我刚刚为什么会提到正方形的内接圆吗?
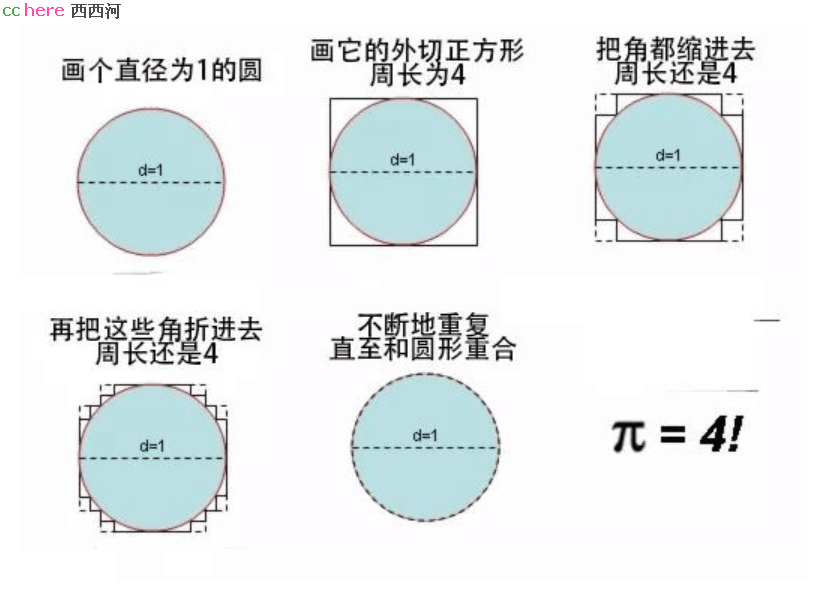
还记得我在前面提出的那个"无论如何总步数都是8步"的问题吗?所以当有人用微积分思想推出π=4之后,马上就会有人跳出来告诉你:正方形无论如何细分都不可能圆弧完全重合的,曲的就是曲的。合着就是某些人说了算,是这样吧?
- 相关回复 上下关系8
🙂啧啧啧,用数学讲歪理 3 日月双华 字226 2024-08-15 02:10:33
🙂谈谈开窍(2) 1 给我打钱87405 字9338 2024-08-12 02:06:14
🙂谈谈开窍 2 给我打钱87405 字6599 2024-08-11 23:17:21
🙂再讲祖暅原理

🙂不用那么复杂,把图2的方格无限细分下去,就有“对角线=两边” 3 fuxd2002 字0 2024-08-14 13:17:31
🙂错就错在那,边长之和是大于斜边的 1 良师益友寻常客 字78 2024-08-15 02:00:45
🙂不同的视觉诱导会得出截然相反的结论 给我打钱87405 字853 2024-08-14 21:34:00
🙂因为第一种情况等价错了 1 良师益友寻常客 字0 2024-08-15 02:02:36