主题：“魔改”《白蛇传》 -- 给我打钱87405

祖暅原理我本人是无法理解的，我说的理解指的是祖暅这个人到底开了什么窍。尽管如此，但还是可以打个9环。

长方形的面积为什么是a*b呢？因为我们就只知道如果a变成了2a，那么面积就会变大一倍，把a换成b也是如此。这就意味着，面积公式只是在描述正比关系。可是，你有没有发现圆的面积公式有点奇怪，它是k2*r^2。这里插一句，有个别读者看不懂r^2这样的书写是什么意思，这里我说一下。^2就是平方的意思，目前的电脑系统只能这样，你想看到你所熟悉的那个平方的写法，就得转换成图片或者是用更为高级的文字编辑软件然而QQ、微信什么的都不支持。

现在说回来。长方形的面积公式是a*b，圆的面积公式是k1*r*r，这似乎没有什么奇怪的啊，正方形的面积公式不也是a*a吗？正因为你不奇怪，所以你开不了窍。

长方形如果只变其中一边，它就会发生变形，正方形也一样，可是，在我们一般的意识中，圆只有一条“边”也就是半径，所以不论如何变，圆始终是圆，换言之，圆始终在做缩放动作。

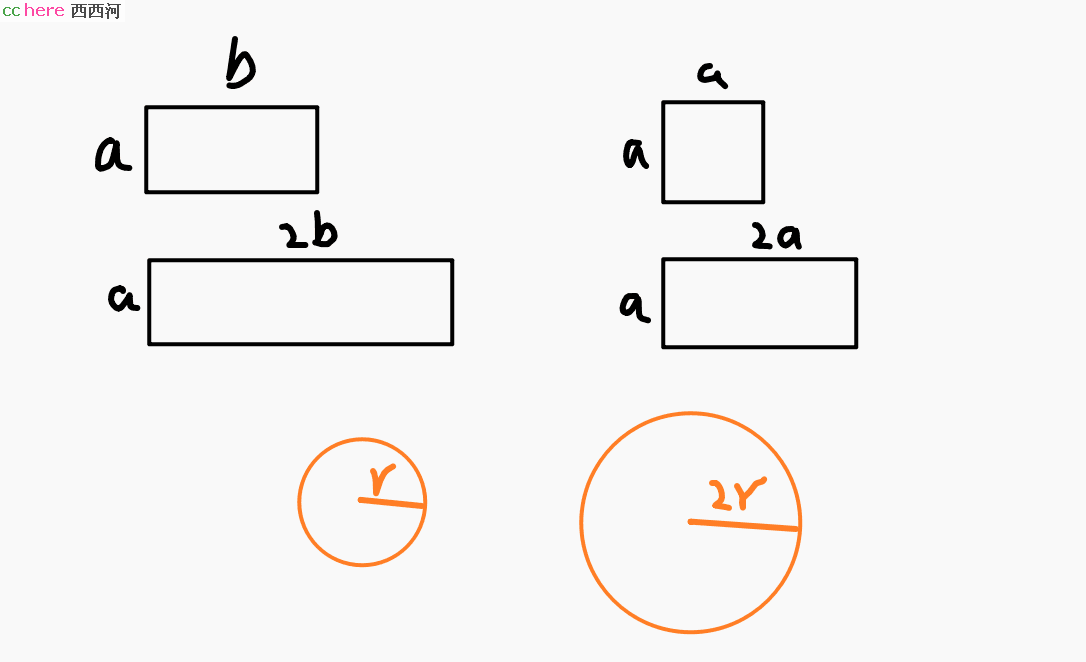
这是规则图形，那不规则图形呢？

不规则图形不存在边的概念，对吗？因此，当我们谈到不规则图形时只谈缩放。地图就是这样，有不同的比例尺，比例尺是在描述缩放的程度。

我说到这，你有没有猜到我下句话讲什么？

圆，是不规则图形中的特殊情况。如果我们只考虑缩放，圆就是不规则图形中的特殊情况。

我在前面提到地图和比例尺，因此你也可以把圆视为地图，想把一个圆放大或缩小，也可以用打格子的方式把原作搬到另一块画布上面来，我说的是手绘哦。

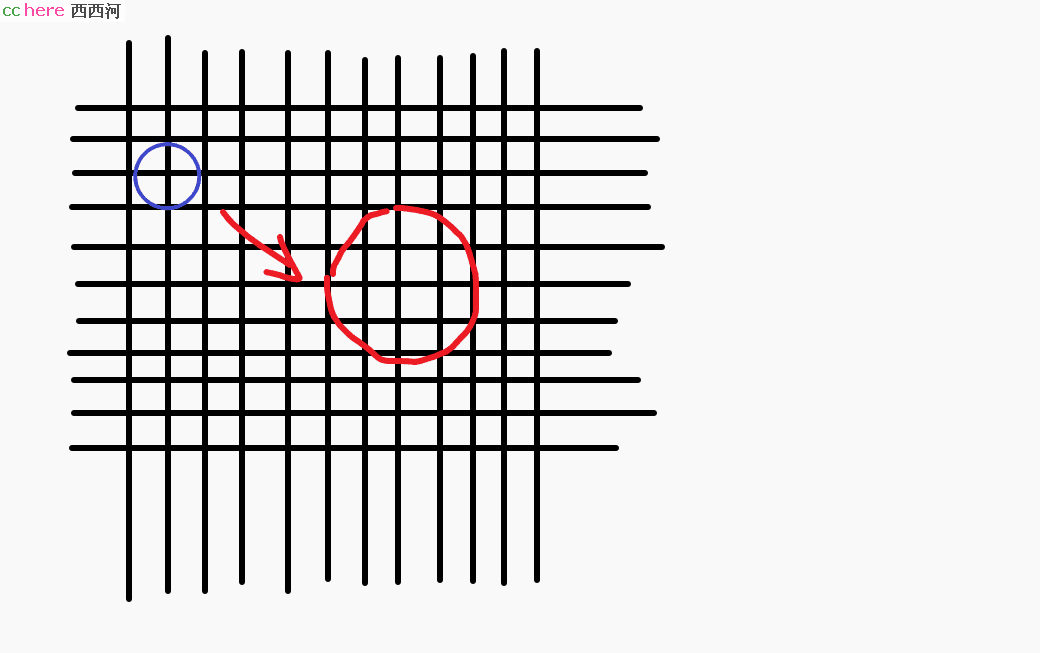
小圆是直接画出来的，你可以当成我是用圆规作的，大圆是手绘的。注意，格子本身没有变化，我只是改变了所使用的格子的数量。我记得郭富城拍过一部电影，他演的是一名名画赝品制造者，他所使用的方法就是我刚刚用的方法。电脑是不一样的，电脑是先把原作转换成横平竖直，再利用高分辨率完成视觉欺骗。为什么高分辨率的扫描仪要贵上许多呢？就是这个道理。扫描，就是化曲为直，因此，像素点也就是正方形小格子越小，扫描出来的结果越是逼真——尽管始终都是横平竖直。为什么我们在网上找到了一些扫描版书籍十分费眼呢？原因就是扫描仪的分辨率低，因此你看到的文字、符号更为马赛克。现在如果只是扫描文字就不用扫描仪了，我们现在有了OCR。OCR的本质是电脑根据拍到的【图片】来猜是什么字，显然，这得有大数据支撑；显然，汉字容易猜对，英文容易猜错。

如果只是考虑缩放之后的面积而不考虑形状那么就要容易得多，找出“半径”来就可以了，这就是重心的由来，对于不规则图形而言，其重心对应的就是圆的圆心。重心对于图形而言，其【相对位置】是不会变的，这就是依据。

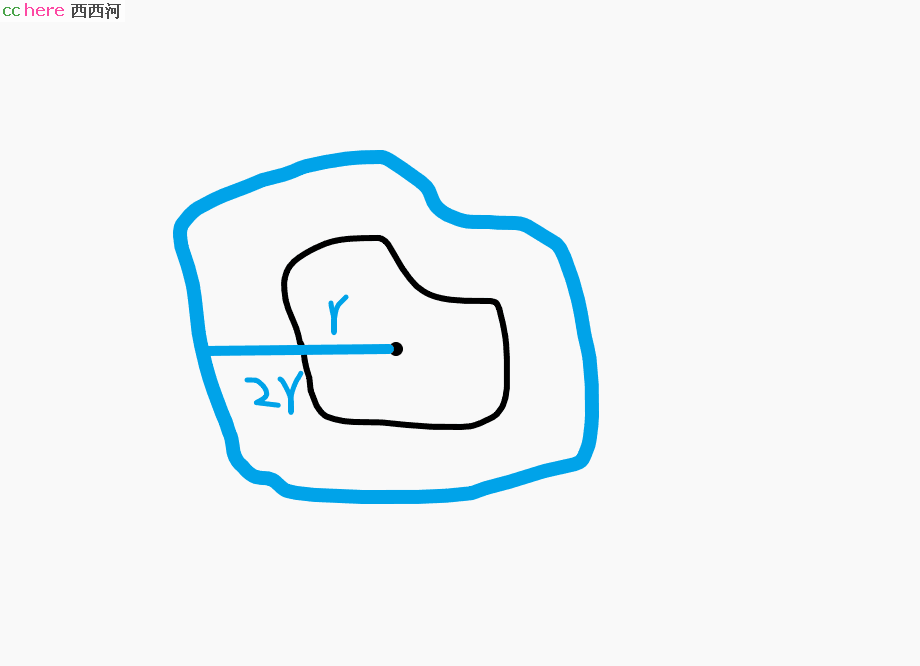
这是一方面。另一方面，圆又属于规则图形中的一员。可这又是为什么呢？

椭圆，椭圆的面积公式是k*a*b，你看，a和b又回来了。

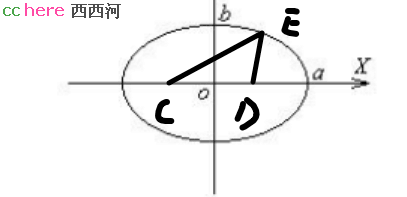
椭圆的面积公式中的a和b，指的椭圆的长径和短径，它有两个，不像圆那样【看起来】只有一个半径。这是为什么呢？为什么椭圆是扁的呢？因为椭圆就是一个动点E到两个定点C和D的距离和不变的运动轨迹。自己想画出椭圆很容易啊，如下图：

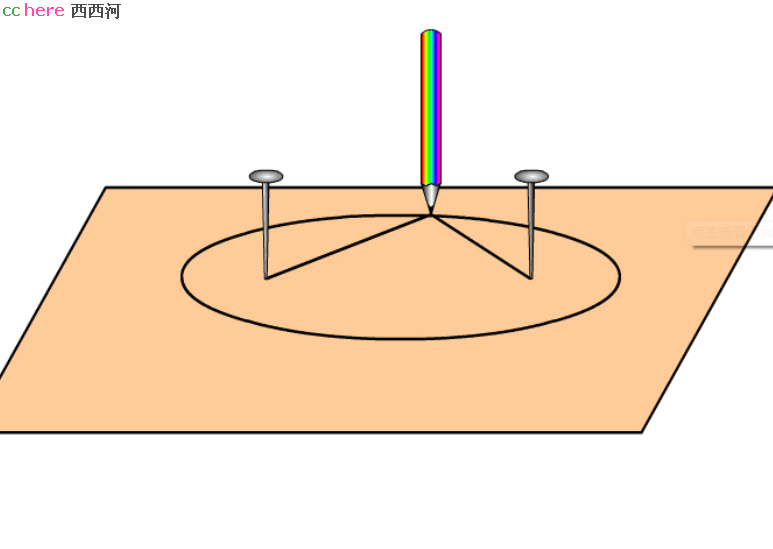
将一根绳子分别绑在两个图钉上，你这么一转，椭圆就画出来了。因此，有两个因素在影响椭圆的形状，一个是两个定点之间的距离，一个是动点到两定点的距离和。圆就是两个定点之间的距离为0，两个定点重合到圆心上来了，所以它不是扁的，圆的直径也就是动点到两个定点的距离和永远被平均分成了相等的两段，即半径。两个定点之间的距离影响的椭圆的“扁度”，两个定点分得越开，两者之间的距离越大，椭圆越扁，反之越圆。动点到两个定点之间的距离和影响椭圆的大小，这个距离和越大，画出来的椭圆越大，反之越小。

顺带说一句，见过别人玩空竹吗？这里面就有椭圆和图的哦。

也顺带提一句，椭圆的面积公式是k*a*b，这个k我们所学的就是π，你看，这个π的影响有多大啊。

说了这么多，我其实就想说一句话，圆有特异性，它是跨界选手，它既可以算到规则图形阵营中去，也可以充当不规则图形的旗手。

看到现在，你可能会认为我所说的跟祖暅原理没有关系。嗯，所以我才打中了9环嘛，9环跟10环并不是你认为的那样只差一丢丢，而是天差地别。

就是说，对于一个不规则 的立体或者是一个规则的立体然而不知道它的体积有多大，怎么去求出来呢？你得找到特异性才行。特异性指的就是某某是跨界选手，只有这个某某才能把规则和不规则联系起来。微积分是这么思考问题的吗？显然不是。西方人说的是无限细分，曲就变直了。

祖暅原理说，若两个立体等高，只要是在任意同一高度的横截面相等，那么这两个立体的体积就是一样大的。我有100%的理由认为祖暅找到了特异性，但我不知道这个特异性是什么。我的子弹上靶了，但只能打中9环，10环到底是怎么回事这得去问祖暅。

就写这么多吧，我有想表达的东西但我【现在】表达不出来。

另外，你有没有注意到我在最开始说明^2表达的是平方时用到的图片是这张：

我是特意挑出来的，你注意到自然数平方和右边那个式子的第一项系数是1/3了吗？你把这个1/3跟棱锥、圆锥体积公式里的1/3联系起来吗？你有注意到是自然数【平方和】吗？其它的我就不说啦，我就告诉你1/3是怎么来的，嘿嘿。