- 近期网站停站换新具体说明
- 按以上说明时间,延期一周至网站时间26-27左右。具体实施前两天会在此提前通知具体实施时间
主题:【原创】“罪大恶极”的数学家 -- 潘承彪 -- 萨苏
都是非常牛的吃饱了撑的人。他们穷数年,十数年,数十年,乃至于上百年要证明的东西都是明摆着的。
比如说,两点之间直线最短。是个人就明白,甚至连条狗都理解,数学家们还要去证明?!还费好大力气去证明。
再比如说,两条直线交叉有一个交点,明摆着嘛。居然有数学家证明出能有好多个交点,还有更吃饱了撑的数学家证明不可能有交点。
![]()
以高三中学生的能力,对数学中的循环论证深刻体会,再实战应用避免在高考考卷上,难,难,难!
当然,某上贴也是调侃。
终于证出来了,![]()
问题是现在还没证出……![]()
![]()
这是1979年的高考题。那时侯,是高中两年制,还没有高三的学生呢。![]()
按萨老大的说法,本人还是那1%的人罗。其实想到了就很简单,用相似三角形去证明就成了。当时只是自认几何学得还可以,所以想都没想就用了几何的方法。考完后下来才知道,很多人都用解析几何的“两点之间的距离”公式去证明,却忘了这个公式的基础就是“勾股定理”,正好中了老先生的圈套。![]()
20多年前﹐ 大學招生率只有百分之沒多少﹐ 每道題都很難﹐ 沒有幾道題做對的考生能超過百分之幾的。 ![]()
以中學生的知識水平和經驗﹐ "空手套白狼"地去證明勾股定理﹐ 確實很難﹐ 但通過學習後﹐理解和掌握勾股定理的證明並不算難﹐ 標準中學教科書和教學提綱好像(?)都非常強調勾股定理的證明﹐ 學生很應該重視。 勾股定理的證明﹐ 是高中階段的平面幾何甚至代數的一個很好的﹐ 有指導性的例子﹐ 至於勾股定理背後深奧的東東﹐ 則完全與高中學習或高考無關﹐ 潘老師本意也許打算來一道送分的題 ﹐ 正如萨老大在1樓所說的﹐
"。。。他认为中学教育不能只注意题海和数学竞赛,而且应该在基础方面让学生打得更扎实一些,。。。"
![]()
---老骨依然硬---
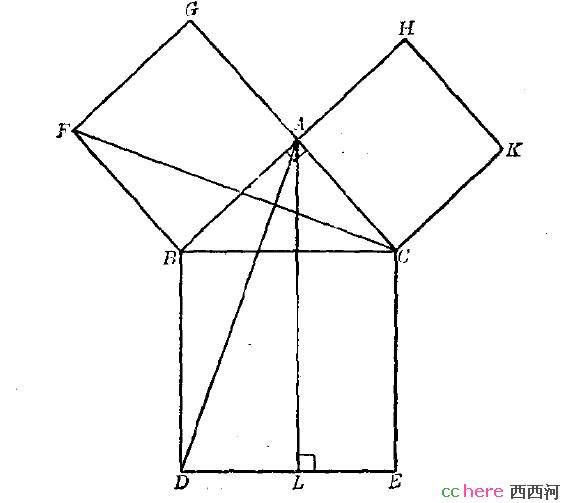
三角形ABD全等于三角形BFC
正方形BG面积等于矩形BL面积
剩下的就容易了。
这个题只有几何解,没有解析解和三角函数解。因为解析解和三角函数解是以勾股定理为基础的。那是循环论证。
几何解也有好几种,不过高考时,很少要求这样基本的几何学考题。学生们很容易懵掉倒是真的。
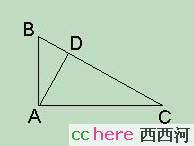
用相似三角形证.
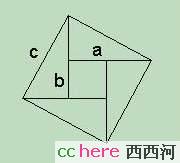
用正方形面积证.
分析? 或是指动力学/微分方程中的Bifurcation(分支/分叉)?
杨乐,张广厚是搞函数论的吧.
数论还有王元.
好奇...