- 近期网站停站换新具体说明
- 按以上说明时间,延期一周至网站时间26-27左右。具体实施前两天会在此提前通知具体实施时间
主题:【原创】结还是离,这是个问题(一) -- 老马丁
小鸭吃奶后不哭不闹,正好让daddy把坑填完。
人海之中,找到了你,找到了痴爱所依。这是歌里唱的。现实一点吧,这世界上哪有这么容易的事?俗话说,易得无价宝,难得有情郎。vm=vf是绝美的搭配,如果vm=0.9vf呢?就能不能凑合一下过过?于是作者的分析转到结婚的决策上来。
结婚的决策取决于结婚和不结婚的比较。这里不考虑很多人关于结婚的决策取决于自己结婚的情况和别人结婚情况的比较(攀比)。假设不结婚带给人的效用为一个常数。
做图,横轴表示vm(男方类型),纵轴表示效用(在图中。上面提到的在一致离婚制度下期望效用和想离就离制度下的期望效用都是一元二次方程,初中三年级的数学告诉我们,他们的图像是抛物线,在这里因为都取得极大值,所以是顶点在上的抛物线。根据(中)的分析,两抛物线的顶点都在vm=vf上。不结婚则为一水平直线,因为该效用不随潜在的结婚对象的类型改变而改变(错过一个金龟婿和错过一个陈世美没有区别)。那么初中数学告诉我们该水平线和两抛物线都相交于两个点(对这两条抛物线来说这两个交点都是不同的,所以共有四个有意思的交点,从左到右,依次为a,b,B, A)。在这两个交点间,在对应制度下结婚的效用值都大于不结婚的效用(因为在两点间抛物线都位于水平线上)。
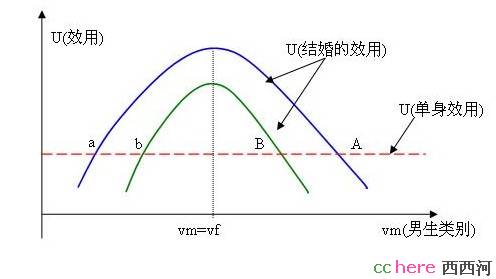
我们先粗粗的定性分析一下。对某一条抛物线来说,这两个交点说明什么问题?这两个交点中较小的一个(a或b,在左边)表示的可结婚对象的类型的下限,低于这个点的vm类型都是不太重视婚姻的男士,女方当然不愿意和他一起生活。较大的那个交点(A或B,在右边)表示的可结婚对象的类型的上限;高于这个点的vm类型都是太重视婚姻的男士,女方也不太愿意和他一起生活。人也是矛盾的呀。 在aA或bB间类型的男士,对该女生而言才是理想的结婚对象。虽然很难找到vm=vf的最优,但是找一个aA或bB间的次优也不错。
还有一个重要的问题没有回答。那种离婚制度下结婚的效用高?换句话说,这两条抛物线的关系如何?谁在上谁在下?结果是,这因女方(决策方)的类型vf而异。那么具体来说,如果女方的结婚价值不大(vf<0.5),大家猜一猜,那种制度下这位女同志的结婚的效用会更大?
本帖一共被 2 帖 引用 (帖内工具实现)
- 相关回复 上下关系8
🙂有道理 3 老马丁 字586 2007-09-25 21:18:03
😉不懂也要花,支持老马! 1 梁东 字0 2007-09-25 19:41:41
🙂例花,例沙发! 1 马头磬 字0 2007-09-25 19:34:55
🙂【原创】结还是离,这是个问题(三)

🙂送花给教授,马丁教授 2 路边野草 字58 2007-09-23 16:27:26
🙂关于经济学中的假设有个笑话 4 四不像5 字683 2007-09-20 19:51:51