- 近期网站停站换新具体说明
- 按以上说明时间,延期一周至网站时间26-27左右。具体实施前两天会在此提前通知具体实施时间
主题:【原创】化工过程控制的实践 -- 润树
在MPC一章里,出现了动态和静态优化的概念,也就是根据MPC的线性模型来计算过程最佳静态操作点和到达此点的动态途径。但是由于其模型没有全面地(MPC的变量只是过程所有变量的一部分)和准确地(忽略了过程的非线性)反映过程的特性,只能说它是一个片面/局部和近似的优化。
所谓过程静态优化(PSSO,process steady state optimization)则是一个远在MPC之前很久就出现了的古老命题:
给定过程的目标函数 J = f(x1, x2, x3, ……, xn),在x的约束条件下,找到优化变量x1, x2, ……, xn的值,使J最大化或最小化。
传统上,有两种方法来实现PSSO,一是通过过程的数学模型来计算(模型法),二是在线搜索(搜索法)。模型法中用到的模型,既可以是基于第一原理的机理模型,也可以是经验模型,或两者的结合,在MPC之前,大多是离线实现。也就是说,通过人工或计算机的计算,找到最佳静态操作变量的设定值,然后手动改变这些变量来实现优化。有了MPC后,PSSO所计算出的最佳变量设定值通过这两个系统间的接口传递到MPC自动实现。因此,PSSO可看着是位于MPC之上的一级控制系统。而在线搜索法则是直接改变优化变量的设定值,然后观察目标函数的变化方向,一步一步地去逼近最大/最小值。
最优化,从本质上说是一个数学问题,我们在高等数学中都学习过了。对于线性和低阶的目标函数和约束条件,可以用求导数和代数的方法来求解,而对于高阶和非线性的目标函数或约束条件,则需要用到更复杂的数学方法,像单纯型法,非线性最小二乘法(NLLS)non-linear least squre),分步二次规划(SQP,sequential quadratic programming),总体降梯度法(GRG,generalized reduced gradients)等等。MATLAB之Optimization Tool Box是用来求解此类问题的好工具。但这里我们不对这些数学方法作进一步的讨论,而将焦点放在过程优化的含义及其具体的工程实现。
我们先来看一个精馏塔。如图4.0.1所示,这个塔的操作目的是将进料中的二元主分Ca和Cb分离成塔顶的轻主分和塔低的重主分产品。一般地,这个分离过程是非理想的,即塔顶会有重主分杂质Xb,而塔底也有轻主分杂质Xa。现在的问题是,怎样的分离才算经济上最优。
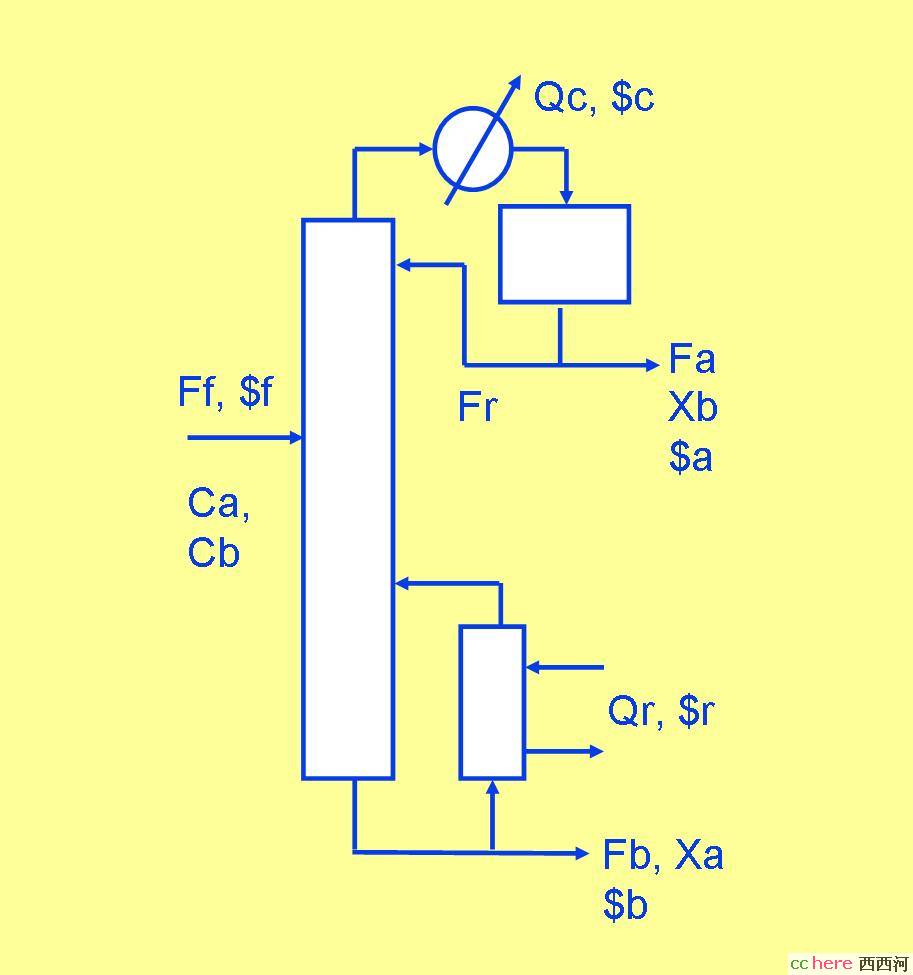
图4.0.1 二元精馏塔的分离示意图
我们可以定义这个过程的优化目标函数如下:
J = 产品所得 – 原料成本 – 能源成本
= Fa*$a + Fb*$b - Ff*$f - Qc*$c - Qr*$r (1)
式中,
Fa和$a – 塔顶产品流量和价格
Fb和$b - 塔底产品流量和价格
Ff和$f – 进料流量和价格
Qc和$c – 冷凝量和价格
Qr和$r – 再沸器热量和价格
约束条件是:
塔顶和塔底的杂质主分小于产品指标值 Xa <= Xa_spec, Xb<=Xb_spec (2)
冷凝器和再沸器能量受限于最大设计值 Qc <= Qc_max, Qr <= Qr_max (3)
由该塔的物料平衡,我们可以得到:
塔顶产品 Fa = Ff (Ca-Xa) / (1-Xa-Xb) (4)
塔底产品 Fb = Ff (Cb-Xb) / (1-Xa-Xb) (5)
对该塔的能源消耗,我们有经验公式:
冷凝量 Qc = Ff (c1 + c2*Xb + c3*Xb*Xb) (6)
再沸热量 Qb = Ff (d1 + d2*Xb + d3*Xb*Xb) (7)
将(4)-(7)代入(1),可得
J = f(Ff, Ca, Cb, Xb, Xa, $a, $b, $c, $r) (8)
在给定Ff, Ca, Cb, $a, $b, $c, $r的情况下,(8)式中只有Xa和Xb是优化变量,而如果塔底产品价格高于塔顶产品价格,即 $b > $a,那末Xa应控制在其上限(低价值组分作高价值产品),就是所谓的卡边操作。这样就只剩下唯一的优化变量Xb,可以很容易的算出它的优化值是15%,其对应的最大值J是$1006/小时。既然b主分价值高于a主分,为什么不尽量将这个数值控制在最小值呢?这是因为,要获得那样的结果,就需要加大回流量,导致冷凝量和再沸热量的消耗都上升,而抵消或超过由更多的塔底产品所带来的经济利益。图4.0.2是用MS Excell计算的图像显示。顺便说一下,MS Excell里的Add-Ins Solver也可以方便地用来求解复杂的优化目标函数。

图4.0.2 优化分离的图像显示
这个例子很间单,旨在用来说明化工过程中优化概念。实际的情形要复杂得多,我们将在下一节用Aspen Plus 的Real Time Modeling and Optimization来详细考察。
这里提出一个数学上臭名昭著的Banana函数优化问题,有兴趣者不妨用MS Excell里的Solver去求解一下。当然用其它方法也可以。
J = 100*(X2 – X1^2)^2 + (1-X1)^2
求解J的最小值,无约束条件。^2是平方算子。
- 相关回复 上下关系8
🙂有意思 1 爱莲 字48 2007-11-14 18:07:41
🙂线性代数理论发展和应用较晚 润树 字34 2007-11-15 20:16:00
🙂大夫,你们学校你的专业 喜欢喝冰茶 字46 2007-11-14 20:59:07
🙂【原创】4.过程静态最优化(PSSO)

🙂请教下列公式的来源和物理意义 1 罗博 字171 2007-11-12 18:52:47