- 近期网站停站换新具体说明
- 按以上说明时间,延期一周至网站时间26-27左右。具体实施前两天会在此提前通知具体实施时间
主题:【原创】电力系统漫谈 (一) 引子 -- 乃力
麻雀虽小,五脏俱全的道理在电力系统并不总是适用。下面这一段介绍的最简单电力系统的稳定性分析并不能自动引伸到实际系统。但是,从这个小系统里,我们大体上能得到一些对大系统稳定的直观认识。照着猫去找老虎,虽然差得远了些,但还是勉强能和熊区分开的。
对暂态稳定研究来说,最简单的系统就是如下图所示的单机无穷大母线系统。中间是两条输电线路,一边是一台发电机,另一边是永远静止的无穷大母线。这个系统有些象在楼顶上挂个小气球,不管气球怎么随风而动,楼一般没事,最多就是气球飞上天了。
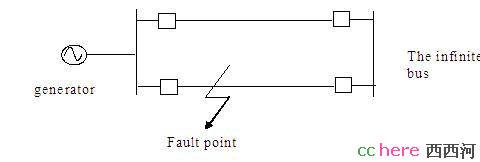
图1 单机无穷大母线系统
进一步假设,无穷大母线电压是V,电压相角是0;发电机母线电压是E,相角是θ;每条线路的阻抗是X。两条线路并联,阻抗就变成了X的一半,暂且用Z表示吧。对这样一个系统,发电机送出去的有功功率是多少呢?闲话少说,直接给出公式:
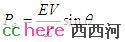
前一节提到过,计算能量函数除了需要找到不稳定平衡点,还要计算电气功率和机械功率的差。上面的公式就是单机无穷大母线系统的电气功率,是电压相角的函数。再考虑到系统稳定运行时,机械功率和电气功率相等,那么,
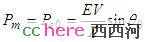
其中,θ0是系统稳定运行时发电机电压的相角。现在假设在其中一条线路上发生短路故障,发电机电压E瞬间减少到几乎是零(取决与故障点离发电机的距离),这时候发电机的电气输出功率也变得很小,但也可以用类似的正弦函数表示。在暂态过程中,相角会改变(想象一下,一阵风吹过,那只气球会怎么样?),但可以假设机械功率不变。如以前讨论过的一样,发电机这时候会开始加速。故障线路很快会被打开以清除故障,只剩一条线路运行,但电压回升,输出的电气功率也开始回升。因为线路的阻抗变了,发电机的电气功率此时变成了:
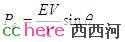
因为系统简单,电气功率能直接表示成是电压角度的正弦函数,我们可以把这些函数画到图上。这就是电力系统里著名的功角曲线。横轴是电压相角,纵轴是功率。水平直线是机械功率,三个曲线分别是对应不同状态时的电气功率。图中机械功率和横轴之间的两条长竖线,做左边的标识出了故障发生前的系统运行点,右边的则对应故障切除时的系统运行点。
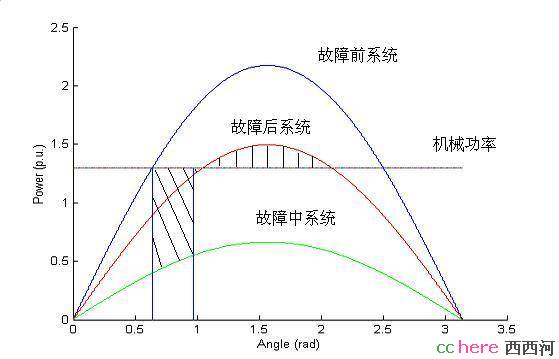
图2 功角曲线
大家不妨试一试把斜线阴影区域和竖线阴影区域的面积写成功率对相角积分的形式,看看会得到什么?
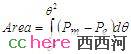
看着很熟悉吗?这是不是我们 前面看到过的势能呢?答案是肯定的,来比较一下势能的公式就知道了:
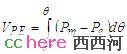
因为故障中的电气功率计算很不准确,计算斜线阴影区域的面积是没有意义的。所幸能量守恒定律再次给我们指明了方向。还记得那个坑底的小球吗?这次我们让它从左侧滚下来。球在坑底时的动能等于它在左侧开始下滚之前的势能。
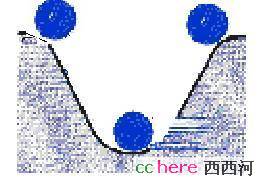
图3 滚落的小球
同样道理,在故障切除那一时刻的系统动能也正好等于斜线阴影区域对应的势能。故障切除时的系统动能前面也介绍过了:
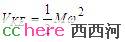
这样,斜线阴影区域的面积等于故障给系统注入的动能,竖线阴影区域的面积则相当于小球爬上右侧斜坡后具有的势能。如果这个势能小于球在坑底时的动能,小球将离开这个安乐坑。对这个电力系统来说,如果斜线面积大于竖线面积,就不稳定了。现在,判断系统是否稳定,变成了判断两个面积哪个更大。而这个判据正好和前面介绍的能量函数法完全等价。这就是学电力系统的人都熟悉的等面积法则。斜线面积又叫加速面积,竖线面积又叫减速面积。故障后系统功角曲线和机械功率的交点,左边的是稳定平衡点,右边的是不稳定平衡点。多么和谐,多么对称的电力系统!可惜,猫是猫,虎是虎。我们谁也不会抱个老虎坐沙发上看电视,是不是?
不管怎样,从这只小猫身上,我们还是能得到一些有用的信息。除了前面讲的以外,比较重要的有三点。
第一,是对一个给定的系统结构,在稳态时,其电气传输功率有个上限。对这个简单系统来说就是电压相角为90度(正弦为1)时的功率。
第二个是,输电系统的阻抗对输电功率上限有重要影响,阻抗越小,上限越大。怎么减小阻抗?要么缩短线路长度(也叫电气距离),要么加粗线路导体或几条线并联,要么用其它办法。什么叫其它办法?比如说,高压线路的阻抗比低压线路的小;再比如说,线路自身是个大电感,我们可以串联进一个电容,正负抵消。那超导行不行?
第三个是,增加稳态时输电功率的上限,可以提高系统的暂态稳定性。比如说,把功角曲线中故障后曲线升高的话,减速面积增大,系统也更稳定。这样一来,我们知道了一个增加系统暂态稳定性的方法:减少输电路径的电气距离。一个自然的推论就是长距离输电天然地不利于系统稳定。
本帖一共被 2 帖 引用 (帖内工具实现)
- 相关回复 上下关系8
压缩 2 层
🙂对于实际调度,依赖的是经验 1 乌金沙 字170 2010-02-08 21:21:28
🙂实时运行的时候发生故障,要靠预案 1 乃力 字282 2010-02-08 21:55:18
🙂运行条件发生了深刻变化 1 乌金沙 字187 2010-02-08 23:55:21
🙂【原创】电力系统漫谈(四)电力系统稳定(4)最简单系统

🙂【原创】电力系统漫谈(四)电力系统稳定(3)理论之美 17 乃力 字5674 2008-06-01 00:11:32
🙂又重新学习,加深理解 1 圣V 字154 2008-06-02 01:35:32
🙂瞎说说 1 闲看蚂蚁上树 字72 2008-06-01 22:52:16
🙂你这个还真不是瞎说 1 乃力 字153 2008-06-02 00:00:33