主题：【原创】纳什均衡即为势--对博弈论的分析 -- baiqi

第一次听说这样的提法

牛顿三定律本来就是假设,在不受力的情况下静止或匀速运动本来就是一个大大的假设(在相对论看来也是不正确的假设)

相对论光速恒定也是一个假设,别人问爱因斯坦,你为什么要这样假设,爱因斯坦回答:我找不到比光更适合作为各种坐标系的桥梁的东西,并且我以为,总得有一个这样的东西存在吧(大意).

这也源自波普的"科学只能被证伪,不能被证实"的科学研究哲学观.老实说,个人认为眼界比较宽家中有多些藏书的理工科生,这些都是不言自明的.

孔子只看到了周易，还是失传了一部分。我们看到的易究竟是什么版本就很难说了。

从易来看，主旨是讲不同情形下的不同策略。策略固然重要，然而如何判读当下所处的形势才是最关键的。

周易已经进化到最佳策略制定的阶段，所以如果有商易和夏易的话，应该有对于形势的判读的详细讨论。

你说得不无道理，果直如是，三本的价值都极其珍贵，亡失两本，甚为遗憾。但这两本没找到之前，一切都只是猜测。

你举的这个例子，诠释当中有不少需要补充的内容，正好博弈论是我的论文方向，而我导师也有一篇很有意思的文章研究过石头剪刀布游戏。

首先，“如果没有混合策略模型”是个超级大的假设。这三个策略是如此的对称，因此最有意义的均衡自然是每个玩家以1/3，1/3，1/3的混合策略参与游戏。你提出的其实是一个已有不少理论研究话题，即有多个Nash Equilibria时的Equilibrium Selection问题。因为某些原因settle在某个特定的均衡上（如两人出包）是可以的，但是需要一些额外的东西来break the symmetry，比如你提到的熟人之间的默契，类似于focal point的解释。

接下来说那个自然的混合策略，我导师提出的问题是，真的就必然要收敛到这个混合均衡吗？回答这个问题需要之前game theory没有太多深究的一样东西，即off equilibrium dynamics：玩家在尚未到达均衡之际（其实大部分时间都是off equilibrium的）是如何对别人的策略做出反应的。简单说一下结论，如果是个good Rock-paper-scissors game（比如赢了得1，输了扣0.5），那么混合策略是收敛且稳定的；而要是个bad Rock-paper-scissors（赢了得1，输了扣2），那才有趣，不收敛，且只要稍有扰动就会奔一个围绕着1/3,1/3,1/3打转转。

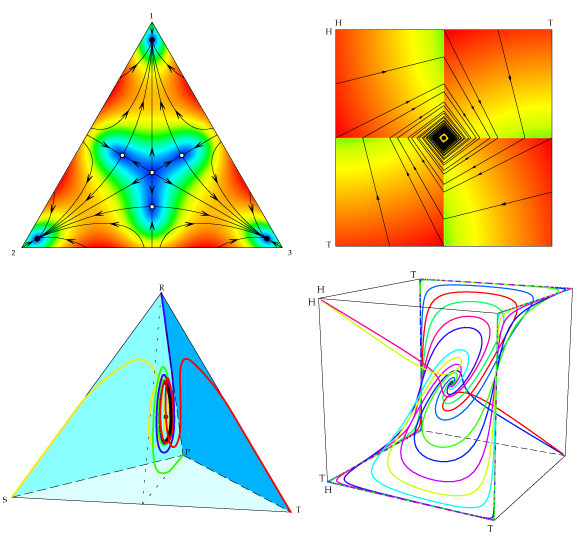
注：上图仅左下角的那个金字塔描述了RPS game,其他三张无关本主题，请忽视。

而且如果是带平局的Rock-paper-scissors，混沌可以观察到。

我有個cornell的朋友就是做power law的社會心理學研究的.人類都有羊群心理. 容易出現正反饋的現象,就是越多人這麽做,其他人也容易做.

其实是我的失误，在混合策略下的均衡点就是一个概率向量（p1,p2,p3,q1,q2,q3),在一般的包剪锤游戏中为(1/3,1/3,1/3,1/3,1/3,1/3).熟人之间产生经常有相同的出拳情况，应该是另有解释。比如说在重复博弈时pi,qi不断的变动，最后产生了p(A出某拳【此拳与B相同】|B出某拳）的概率十分大，在无穷次重复博弈时，概率为100%。这个也可与纳什均衡无矛盾，他们出各拳的概率为1/3,但是出相同的拳的概率为1.但是这个具体是怎么来的，真应了你说的那句，要考虑“玩家在尚未到达均衡之际（其实大部分时间都是off equilibrium的）是如何对别人的策略做出反应的”。如果你有什么见解，请不吝赐教。

另外一个，不光是你这儿提到的，混合策略模型中重复博弈不能趋于绝对理性人一次博弈得到的结果；其实重复博弈相比一次博弈产生了质变，普遍会得到不同的结果。

例如囚徒困境，如果是重复博弈的话，那么囚徒会认识到合作的可能性，并试探之。如果某个囚徒采取一报还一报的策略（1.第一次是合作2.以后每一次视对方上一次是合作还是背叛来作出决择：对方上一次与我合作[即两人都不招供]我这回就合作，上一回背叛我，那么我这回也要背叛）那么如果有n个囚徒两两重复博弈，这一策略却是得分最高的。

所以重复博弈、多人博弈都带来了游戏的质变。

你给出的链接我看了，你要阐述的主旨大体明白，但图例还有不懂的地方，尤其是一些字母的含义。另外有个想法，不妨这样思考：重复博弈会带来质变，如果在重复博弈下考察趋进这个问题，事实上整个游戏都变了，不如换成绝对理性人一次博弈，根据你给出的bad rps game的规则，看看会得到什么结果。按照纳什的博弈论，有个均衡解。也就是有个均衡概率向量。而如果变成重复博弈，每个理性人在第一次就产生了均衡解，往后会如何发展呢？重复博弈到底有什么本质的不同？这真是个很大的问题啊。

受到规则的“奖惩”而不停修正自己的行为。

我认为，纳什模型的一个本质缺陷是没有把规则当作博弈本身的一部分，因而是静态的。

如考虑囚徒困境，不能只把囚徒当作一个整体，而是要把警察和囚徒当成一个整体来看，从而得出一个整体的博弈结果--从这个整体结果的趋向来看才合理，而不是把囚徒就看成一个整体。因而，囚徒困境的实质只是一个规则导向的问题--就是您说的“势”。

请您看下我这个根据八卦折腾出来的模型：http://www.ccthere.com/article/3034853。

“你我他”模型，我以为是这个世界运行的本质模型，可以无限推广。

所以，我以为人类社会其实也是有分形的，本质是：

1。所有行为从长期来看都是受到我们未能掌握的天道制约的。

2。人类社会的存在形式

a。目的：拥有更多的“力”

b。方法：尽可能有更多的博弈机会（自由度）。

由此，可以观察人类社会的分形。

不吝赐教！

恭喜：你意外获得【铢钱】八个

鲜花已成功送出，消耗 铢钱 1 个，可能得宝。可通过工具取消

提示：此次送花为【有效送花赞扬，加乐善、声望、帖得花总数】。