主题：【原创】似虎非虎 -- 淮夷

这周从香港去山东，机场航班弄错，许多光阴扔给机场。好在旅途读了一本书，叫作《The Tiger That Isn’t》。这本书出版于2008年，作者是牛津大学的经济学家，安德鲁同志 (Andrew Dilnot)。

此书的名字有点怪，权且翻译作“似虎非虎”好了。

书中所谓“老虎”是一个比喻，说的是原始人类在丛林中生活，看到林间闪过一个五彩斑驳的影子，大脑第一反应就是：有一只老虎，赶紧逃命！

那个影子不是老虎，而是阳光投在树丛中的幻象。一阵风拂过，树枝摇动，叶子飞舞，一瞥之下，恰如猛虎卧荒丘，潜伏爪牙忍受。

进化论的解释是，原始人类的这种错误直觉其实是最合理的。为了提高生存的几率，人脑需要对各种“看起来”危险的模式迅速做反应。假如一个人选择定睛细看，另一个人选择拔腿就跑，也许只差一秒，但后者的生存概率更高一点。

人类离开丛林之后，反而更需要“定睛细看”，而不是原始人的“拔腿就跑”。我们的时代有大量“似虎非虎”的现象，需要多一点质疑。以前聊过《统计狂人》(链接出处)，讨论统计学无所不在的影响，此书的主题恰好相反，它讲的是统计学“灰色”的一面：对数据的盲从和轻信，以及由此产生的弊端。

弊端之一，是人们对数据有一种过度偏好，总是试图在一片迷雾中找到隐藏的模式。

比如当你看到这张图片，你有没有发现一些隐藏的规律？

您瞧出了什么，北斗七星阵，还是九字连环阵？

实际上，唯一的规律是：毫无规律可言。

这个图片的数据，来自计算机模拟的“米粒实验”，实验产生数据遵循随机分布的特性。如果你用手抓一把米粒，向天上抛去，米粒散落地面的分布，基本上，也会呈现这样的特性。

这种随机散布的数据点，有一个常见的现象，叫作“集群性”(clustering)。比如，把上面图片分割25个格子，有的格子只有一个米粒，有的格子有一大堆米粒。

随机“集群性”和现实生活有什么联系呢？

癌症病人的不规则分布，有时候，可以用随机“集群性”给予解释。假如把每一个米粒看作是一位癌症病人，那么，现实中，确实存在着某些地区癌症病人集中，而某些地区癌症病人很少的现象。

米粒实验的关键点在于：集群性的出现，只是随机偶然的结果 ，而非特殊力量使然。

但是，人们总是忽视事件的偶然性一面，而试图为“看似”异常的事件寻各种各样的原因。譬如，某地少有癌症，必定当地水质优良。某地高发癌症，一准儿也有特别原因造成。

2003年，英国的小村Wishaw，发生一起案件。当地村民把一个通信基站连根拔起，基站的业主是通信公司T Mobile，双方为此大闹冲突，争执不下。

村民毁坏基站的原因是，在基站运行的十年内，基站周围500米的20户村民，已经发生了9起癌症。村民直觉是：这怎么能是偶然呢？难道不是因为基站发射的电磁信号，造成如此密集的癌症案例吗？

人们习惯于为某个病症找到罪魁祸首，而真正的“罪魁祸首”，也许只是偶然性。人体是一个复杂的系统，癌症有无数种可能的源头，就像一个米粒最终掉落何方，也是无数因素的影响：手的力量、抛的角度、空气的流动、米粒间的碰撞，等等。除非刘慈欣科幻小说《镜子》里那种“超弦计算机”，否则很难为一个复杂系统找到它的原因和结果。

换个角度，如果癌症的分布不是随机“集群性”，而是在全国各地的人口之间呈现有规律的平均分布，那才是很奇怪的现象。实际上，人们经常低估“集群性”出现的频率和一个“群”的规模，而习惯于高估一件事的“平均性”。

书中提及了一些简单的实验，可以帮读者认识到，即使在很小范围的样本里，“集群性”的发生也会超过人们的预期。

最简单的实验是找一个硬币连续抛30次，记下每一次正反面的分布。作者记下的随机实验记录是这样：

正反反正反反正正反正正反反反反反反正正正正反正正反反反正正正

这个序列一共有15个正，15个反，恰好符合50：50的随机概率。但是，考察数据分布的集群性，这里最大的集群（黑体部分）有6个连续的反，4个连续的正。这种集群结果和米粒实验一样，纯属偶然。

反之，如果你抛了30次硬币，出现“正反正反正反……”这种有规律的序列，那更像是上帝之手了。

所以，有时候，人们对一个事件（比如癌症分布）的统计数字进行过度解读。而有时候，人们走向另一个极端：对统计数字缺乏深度分析，轻易相信。

譬如2005年，英国的放射病防护机构发布了一个最新医学研究，声称：长期使用手机，脑瘤的风险提高2倍。所以，建议儿童不要使用手机。

这个新闻引起英国各大媒体的报道，人们开始恐慌。“提高2倍”的风险，听起来很大，但是，从什么样的基数算起呢？

安德鲁找到了数据源头，Karolinska研究院的科研人员，玛丽亚。玛丽亚说，脑瘤的基数是0.001%，即，如果没人用手机，每10万人有1人得脑瘤。

“风险提高2倍”的意思，在这个案例里，等于提高到0.002%。就是说，常年使用手机之后，每10万人里面多了1个人得脑瘤。

现在您觉得这个风险算大、还是小呢？反正，玛丽亚本人不会禁止她的孩子继续使用手机。

再譬如，当你读到这样一个新闻时，你的反应是什么？“美国的数据显示，超重人群的寿命普遍长于瘦子的寿命，所以超重对长寿是有帮助的。”

这是一个典型的混淆“统计关联性”和“因果关系”的错误。当一个人病重之时，他往往变得很瘦。并非瘦造成了短命，而是疾病造成了瘦。

关联性和因果律的交织，是常见的统计学应用陷阱之一。

这种陷阱，有的时候并不容易认清。比如，一个统计数据告诉你这样的结果：根据学校成绩的统计，头胎的孩子成绩最好，二胎次之，三胎更次之，出生次序越往后，成绩越差。所以，出生次序决定一个人的智力水平。

出生次序和智力，二者的关联性，确实来自英国学校的真实数据，这一点不需怀疑。如果用因果律解释，似也说得通：因为第一个孩子得到家长的100%的教导，所以智力开发最好。到了老二、老三，家长精力变得分散，顾不上这么多，所以智力开发不够好。

我当然很乐于相信这样一个统计学的“发现”，因为我自己就是头胎。

不过，我也认识很多二胎的，聪明程度远超哥哥姐姐。

问题在哪儿呢？这个陷阱，其实藏的挺深。真正原因是：学校的成绩统计是把所有孩子计算在内，这些孩子有的来自大家庭，有的来自小家庭，混在一起比较成绩。

须知，穷人家通常生许多孩子，而富人家只生很少的孩子。

一个学校里，有富人有穷人。自然，头胎孩子的富人比例高一点，二胎就少了点，到了六胎、七胎，恐怕都是清一色的穷小孩。富人成绩好，主要是家庭资源的差异，而不是因为出生次序影响了一个人的IQ。

出生次序与智力是没有因果关系的，二者有的，只是颇具假象的关联性。

这种数据制造的假象，不仅屡屡来自媒体的报道，也来自看似权威的部门，比如政府。

书中提到一个例子，是英国交通部发布的一则官方声明：“交通部在8个地区试点安装了超速摄像头，试点结果是，超速摄像头降低了35%的恶性交通事故。”

政府讲话不一定都是真的。英国也不例外。

如果搜集某个地区每个月份的交通事故，罗列成一个时间序列的数据，那么这种数据往往有一个重要的特征：起伏周期性，就像是股市涨跌一样。

这意味着，除非有足够长的时间序列，足够大的样本量，否则很难证明，事故降低究竟是安装超速摄像头的功劳，还是因为事故频率本来就处于一个下跌周期？

以常识来思考。某一个高危路段，接连发生车毁人亡事故之后，下个月更可能的情况，往往并非事故数量的攀升，而是下降，这或许由于司机行经该路段格外提高了注意力，也许因为被贴上死亡路段标签而导致交通流量下滑。总之，就算政府无所事事，肇事率也会趋向一个平均值，即，事故高峰之后的自然回落。

这种现象，统计学中被称作“回归效应”。

而政府最可能安装测速摄像头的，是什么地区呢？一般都是所谓的近期事故频发路段。所以，英国交通部的声明，要特别打上一个问号了。

安德鲁教授做了一个有趣的实验，来和英国交通部叫板。他找了20个志愿者，每人分配一个路段，充当虚拟管理员。然后每人轮流扔两次骰子，两次点数之和，用来模拟该路段在某个月份的交通事故次数。

由于连续两次骰子，所以一个路段最少事故的极值是2次，最大极值是12次。这听起来有些像是真实的世界。

实验规则是，当一个路段的事故次数出现高峰时（比如10次，11次，或12次），就给那个志愿者发一个摄像头的照片。志愿者带着照片继续扔骰子，无一例外，此后的事故全都下降了。难道可笑的照片也管用吗？

当然，这没什么可笑的，扔骰子是独立随机事件，扔了很多次之后，高点数（高事故）的出现，趋向于一个稳定的相对频率。

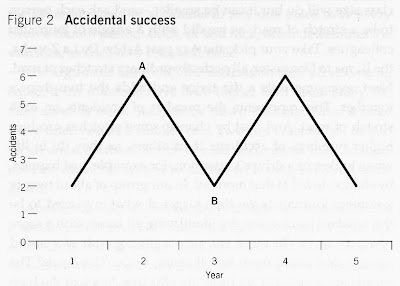
（安德鲁的骰子实验和交通事故次数）

安德鲁教授的实验不止于纸面游戏，他仍不肯放过交通部的数据。对交通部声称的政绩---“安装摄像头降低35%恶性交通事故”，他做了一些实证的分析，结论是：在安装了测速摄像头的地区所减少的事故中，有60%应归功于该路段的回归效应，有18%应归功于趋势效应（即各地普遍性的事故下降趋势，不管有无摄像头）。

他说，抛掉具体路段的回归效应和所有路段的趋势效应，事故下降只有20%的成分或许来自政府的政绩，而这20%也还是存疑的状态。

我认为书中这种“似虎非虎”的存疑精神是值得赞赏的，尤其是，当你看到很多漂亮的统计结果之时。

中国的媒体、政府、企业，越来越多的用数字讲话了，这本身是一个很好的趋势。而另一方面，每个人也该多一点甄别力。

所谓，乱花渐欲迷人眼，看清一件事，有时候挺难的。

原因带来结果，结果反过来又会影响原因的反馈系统。

今天还有很多人都喜欢说“事实”，大致也是落入相同的思维陷阱里了。其实毛时代所说的求实，主要指的是一种精神（即在实施过程中不惜力地仔细观察反馈随时准备调整）；今天的人却大多片面理解为一种行为准则，认为一切事物都应当遵循某种“基准”或“真理”。殊不知现实中可以“不见兔子不撒鹰”的状况是少数，多数情况下都需要对情况不完全明了的情形下快速决断。那么决断对了就高叫英明神武，决断错了就大骂祸国殃民吗？

看清一件事物都是不容易的，喜欢放马后炮的人总可以在事后充充诸葛亮，设计出一套最佳方案。可真要换作当时的环境，谁能真的就会采取那个所谓的“最佳”吗？英雄人物之所以为英雄是能人所不能，马后炮们如果事事都有最佳路线，何必还需要在网上放炮，现实中有的是机会充英雄或先知。

Karolinska研究院的人要有多大的样本空间才能有这个结论呢?

很多统计结果就是因为自身的涨落而导致骇人听闻的结果的

所以，再采用他们的结论的时候呀特别小心。尤其是医疗保健社会现象这种准确采样非常困难的现象。

把一些搞的非常清楚的恶果是，人的愉快程度大大的降低了。特别是男女之间的好感大部分可能是误会产生的。钱财对人得吸引力远高于其他的人品因素，许多大家都愿意摈弃，但是确实是生活里的主导因素。

统计分布背后都隐藏着概率，重要的统计量除了常见的平均值之外还有方差，方差越小实例偏离平均值的可能性越小，不给方差的统计分析很无力。兄台引的例子基本都是不考虑方差的统计分析，呵呵。另外，相对少的观测次数会表现出更大的偶然性，拿丢针实验来说，100*100的格子丢100个针，各个格子上的针的相对数量会差别很大，差几倍很平常，但是丢1亿或者10亿根，相对数量的差别通常会非常小。

老虎对于原始人类，是强大而不可控的因素；杯弓蛇影草木皆兵的反应被兄台所认可。同样的，电磁辐射对现代人来说也是强大神秘和不可控的因素，但是‘20户村民，已经发生了9起癌症’之后，拆除基站却被兄台认为是过度反应。呵呵。

这种偏好是因为我们面对的是未知的世界，从其中找出规律是理所当然的反应。丢针那个例子，背后也不是没有模式没有规律--它正是平均分布的一个实现。当年人们在永动机上花费了无数聪明才智无数人力物力，然后才有热力学第二定律的举世公认。是不是过分迷恋数据，很难给一个黑白分明的判断。

至少两个统计峰要落到对方的一个方差之外

主要指的是一种精神（即在实施过程中不惜力地仔细观察反馈随时准备调整

受教了

追溯要从研究设计开始

专门有一门学科就是研究这个的叫Causality

没有读过这本书，只是从一个经常做数据分析处理的人的角度看问题。比如说，你举的第一个例子，就是那个散点图，对于很多理工科的人来说，规律那是大大的有啊。举个最简单的例子，这个图可以看成是一个5 x 5矩阵，矩阵中的数值为每个网格中存在的点数，如下图所示：

8 5 4 6 9

6 5 2 3 6

4 7 5 4 3

1 8 5 1 6

1 3 3 1 3

计算一下这个网格的均值，为4.36，也就是说单个网格中平均有4.36个点。

既然是矩阵，那么对其做个奇异值分析看看，其奇异值为“23.28519 6.78553 3.35594 1.82084 0.42258”。嗯，这个矩阵不错，不是奇异矩阵，可以用来解矩阵方程，俺们喜欢！

咱们再直观的来看，如果我们对这个5 X 5 的数字矩阵进行平滑平均，即分别用1x1（实际就是矩阵本身）, 2x2, 3x3, 4x4, 5x5（即计算单个网格中的平均点数）的移动窗走一遍，如下图所示：

这张图上，俺使用相同的色标，即深蓝色为1，深棕色为9，当用1x1网格，也就是单看矩阵本身时，怎一“乱”字了得；2X2平滑以后呢，可以看出蓝色区域主要集中在底部，尤其是右下端，这就告诉俺们如果你想去点少点的地方，去右下角找就行了；再用大点的窗口平滑，3x3和4x4都告诉我们类似的信息。举个例子，好比咱们去看山，离远点看，这是一座山（5x5网格得出均值为4.36）；近点，山是连绵起伏的，有山峰，还有山谷；再近，再近，最跟前了，钻到树林里，迷路了，乱花渐欲迷人眼，你怎知身在此山中呢？

再换一个思路，比如说可以用上分形(Fractal)分析的概念，计算一下豪斯多夫维数(Hausdorff Dimesion)，结果大约为1，这说明了从整体上来说，这些个散点的分布接近白噪声分布。

再换个思路，用varigram分析，那内容就更多了。

呵呵，最后再举一例，还可以用频率域分析，比如小波分析。

其实，一个图形只要能转化成数字，那么就能得出很多规律。所以，俺觉得这个例子举得并不恰当，不过作者可能是从科普的角度谈这个问题吧。

噪音信号也是信号。如果是二围图象你总能看出各种形状不同的物体来的。但是他们之间没有啥有意义的关联。

比如车祸、癌症、自杀、脑淤血、心肌梗、暴力、糖尿病等等等等

说实话我一直怀疑加起来的话会大于每年的实际死亡人数。

比如因吸烟而死就是个特别不靠谱的结论。

通过对条件的取舍来得出合适的结论。

拆除基站算不算过度反应，这个确实不能下结论。

‘20户村民，已经发生了9起癌症’之后就拆基站，在没有真正的原因之前这种行为确实属于