主题:【原创】闲谈科学之正多面体 -- 安德的游戏
哈哈,跟正宗鲁皮皮老弟(我读硕士比你早,所以应该比你大![]() )你一样,是搞GPS的。
)你一样,是搞GPS的。
就是讲这些“高度对称的烷烃”,不过他是搞量子化学的,主要是从结构稳定性这方面来解释的。
好像对计算化学(量子化学,理论化学)满熟悉的。
是由所谓的重、轻链RNA编码的。会有高人出来讲这个,期待......![]()
正多面体由于其形态的完美性而受到了古代哲学家们的喜爱。正多面体又被称为柏拉图正多面体,而这个柏拉图就是古希腊的哲学家。他和他的老师苏格拉底及学生亚里斯多德一同被认为是西方哲学的奠基者。柏拉图最早把五种正多面体和哲学联系起来。他认为世界上的一切物质都是由土(地)、火、水、空气(风)四种基本元素构成,而这四种元素就分别对应了立方体,正四面体,正二十面体和正八面体。而剩下的正十二面体,后来被亚里斯多德对应为不存在于地上,而是构成天堂的第五种元素以太。说到以太,又可以引出一大长篇的故事,而对现代科学影响最深的就是光速测量。这个就不是这篇文章的范畴了,等到有机会再挖这个坑。
奇怪的是,中国古代的数学家和哲学家居然没有在这方面有所建树。如果在古希腊的时代中国的先秦哲学家们听说过五种正多面体,他们肯定会把这些东西套进自己的学说里面,尤其是那个叫邹衍的,一定乐得找不到北,认为一共有五种正多面体是对他五德始终说的最好诠释,五行就会被一一对应上。而以后天干地支六十甲子什么的也会往上套吧。
在西方,把正多面体联系到自己的领域最成功的大概要算是开普勒了。开普勒是德国人,曾师从于第谷。后者花了毕生的经历观测星体,把观测的结果交给了开普勒。而开普勒总结这些数据,得到了行星的轨道,提出了著名的开普勒三定律:第一是行星轨道是椭圆而太阳是其中一个焦点,第二是在相同时间内扫过同样的面积,第三是轨道周期的平方和轨道半长轴的立方成正比。这三条是遵从万有引力的二体运动必然能推出的结果,而在万有引力发现之前,开普勒就仅从观测数据得到了这样的结论。在开普勒的时代发现了八大行星中离太阳最近的六颗行星,如何为这六颗行星的轨道找到一个规律令开普勒绞尽脑汁。后来偶然的灵机一动,得到了下面这张被大家所熟悉的图
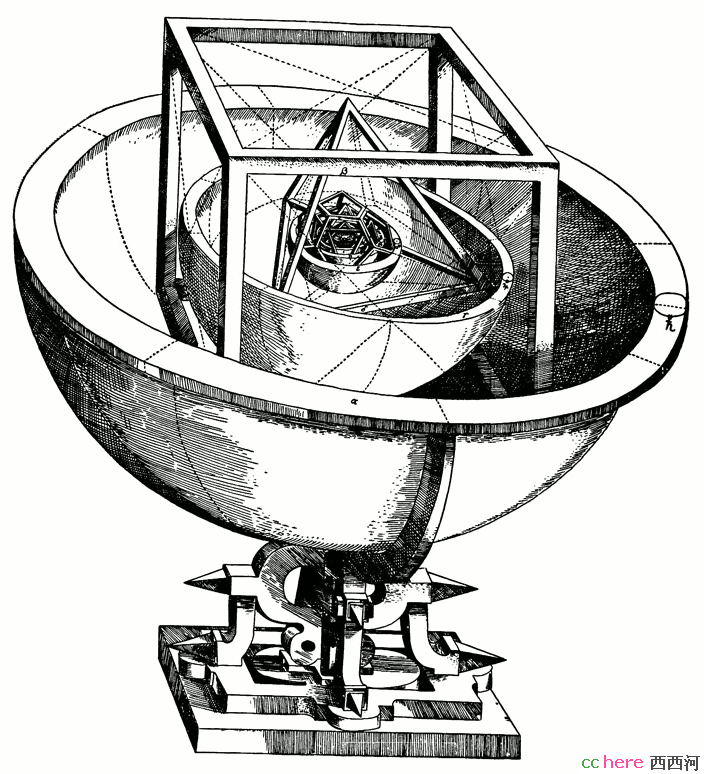
中间部分太小,放大以后是这样的
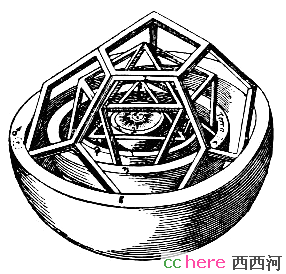
开普勒尝试用六个套在一起的球表示六颗行星的轨道,中间用五种正多面体分隔开。中间的球既是外面的正多面体的内切球,又是里面的正多面体的外接球。这样所得到的轨道精确到什么程度呢?我们做一下计算。
水星轨道和金星轨道半径比例是0.535,它们之间是正八面体,内切球与外接球半径比是0.577。
金星轨道和地球轨道半径比例是0.723,它们之间是正二十面体,内切球与外接球半径比是0.794。
地球轨道和火星轨道半径比例是0.656,它们之间是正十二面体,内切球与外接球半径比是0.795。
火星轨道和木星轨道半径比例是0.293,它们之间是正四面体,内切球与外接球半径比是0.333。
木星轨道和土星轨道半径比例是0.545,它们之间是正六面体,内切球与外接球半径比是0.577。
应该说还是很不精确的。这个轨道模型大概是古代哲学与天文学之间最后的交集了。
顺便说一句,我放狗搜行星轨道半径的数据时,居然google给出了一个链接[url= http://www.tdsrjz.org/message2/20040200049.html]第633讲∶行星螺旋轨道的证明--开普勒椭圆行星轨道批判(雷元星,中共四川省委宣传部退休干部)[/url]。咱们先不说是不是伪科学,这么没有深度没有科学严谨性的东西,居然加上一些科学名词,就披上了科学的外衣,堂而皇之地到研究所的会议室去做报告,还上升到了路线的高度,实在是让我哭笑不得。
本帖一共被 2 帖 引用 (帖内工具实现)
因为各键键能均匀发布,没有哪个键是受挤或者受拉,即便是有受挤或者受拉,最后也能够平衡到均匀发布。
数学上的美,也许就在于此:平衡。
兄弟我不是学化学的,扯两个名词蒙事儿还行,问多了就露出无知的本来面目了。![]()
我不是搞量子化学的,但是以前在基础课上学过一点。
分子轨道(各个原子轨道组合成分子轨道,还是用这个词吧,就不用“杂化”了)在空间的展开,有你说的张力因素,所以“挤”得太厉害的结构能量高不稳定。
这些都是可以用物理和数学“算出来”的,用量子化学(有的地方会运用到群论和对称性的知识)能计算出键能键角键长光谱能谱等等“可观测的量”,然后用计算出的量和实测的量对比,可以部分的说明理论的高明程度。
有机会咱们聊聊GPS?或者Gallileo?
好久以前课本里的了,我不是搞理论的,只能就记忆中的印象说说。
拿碳原子为中心的sp2和sp3轨道来说(前者好比乙烯,后者好比甲烷),西格马键之间的角度就是不一样的,前者是平面分子,键键之间夹角是120度,后者是正四面体(饱和烷烃),键键之间夹角是109度多。
当然我说的这是最简单的情况,实际情况,比如有杂原子(氮磷硫等)存在,有没有孤立电子对,都会使模型复杂化。但是大致上,理论模型上算出来以后,最终是要对到可以直接测量的量上去,键角就是其中之一。
“轨道”这个词的意义在这里已经完全改变了,完全不具备类似“行星轨道”的含义,它是说空间的一块,这一块电子出现的几率最大,也就是“电子云”。
所以,会有“s电子云是球形”“p电子云是纺锤形”这类说法。怎么得出这些“图形”呢?其实这些都是薛定谔方程得出来的。
多电子原子,里面的电子就是分布在这样的“轨道”上。
那么,多个原子组成的分子怎么办?理论上是把各个原子的薛定谔方程“叠加”起来,但是没有办法得出传统意义上的“精确解”,所以,工作大多是通过种种“近似”来做的。直观化,就有“原子1的轨道1和原子2的轨道2叠加出分子轨道.......”等等描述了。
现在设想一下两个原子之间要形成共价键,如果是P轨道电子------既然“p电子云是纺锤形”,那么空间上不同方向的差异就有关键的影响了(“球形的s电子云”就无所谓),这样组合出来的分子轨道,谈论他们空间上的延伸方向就有意义了。