主题：【sos】关于音色 -- 月色溶溶

也来谈谈音色

月色MM提到的这个问题，实际上分为两个方面：一是音色到底是什么（音色的数理描述），二是音色物理上由什么决定。

对第一个问题，简单的回答就是，音色就是声音的波形。也就是说，不论人声还是马叫，或者乐器发出的声音，人耳之所以听出区别来，就是因为各自的波形不一样。也只有不同的波形，才是使音色千变万化的唯一原因。请看下图。

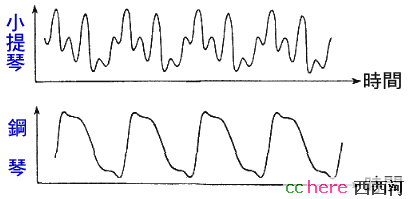
这是一张小提琴和钢琴发出的声音的波形图.只要把麦克风接到示波器上就可以很容易地看到这类波形.

所谓波形,就是波的振幅(即声音的大小)随时间的变化关系.上图的横坐标是时间,纵坐标就是振幅.因此我们也可以说,不同的音色其实就是声音的大小随时间的变化方式不同所造成的.上图是某个小提琴和某个钢琴在发出同一个音符(如中央"C",即简谱里中音的1,2,3,4...中的"1")时的波形对照.此时它们的振幅相同(波的高度一样),而且频率也相同:你看上面小提琴的波形,它是一个具有五个不同高度的"峰"组成的丘形,随时间不断地重复,所形成的.而下面的钢琴波形,则是由一个个不太光滑的"锯齿"状单元不断重复组成.每个锯齿的宽度,与上面每个"五峰丘"的宽度是一样的,技术上称为这两个波的"周期"相同,周期相同就是频率相同,所以它们发出的是同一个音调:中央"C".

大小一样,音调又相同的两个声音,听起来一个是小提琴,一个是钢琴,这其中的差别,当然只是由波形不同造成的:一个是"五峰丘"状,另一个是"锯齿波"吗!

除了乐器以外,其他东西发出的声音,也是由不同的波形产生不同音色的.看看下面两图.

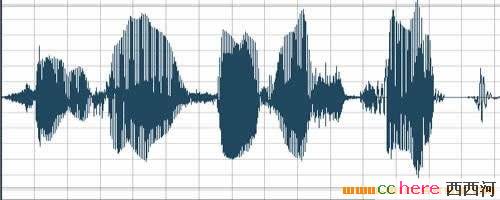
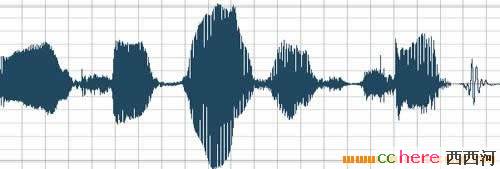
这是一个男声(上图)和一个女声(下图),说出"thank for this..."这一句话时,分别录下的不同波形.说它不同其实也很相似.你看这两组波形的大致轮廓是基本一样的,技术上称之为具有大致相同的"包络线".道理很简单,因为他们说的是同一句话"thank for this".差别在那里呢?差别在于包络线的不完全相同上,以及包络线里面的波形细节上.这两张图太小,如果放大,就能看出这轮廓里的波形细节,其实是有很大差别的.这就是说,波形的大"包络"决定了你发什么音(说哪个字),而包络里面的细节,则决定了你是男声还是女声,是张三还是李四.这就是复杂音频信号的广义的"音色"概念.

总之,什么是音色?音色就是声音的波形,不同的波形听起来就是不同的音色.这没错.但是这句话让懂技术的人听起来,跟废话还是差不了多少.原因在于这只是从直观意义上解释音色,还没有从数学上给音色作精确定义,也无法确定不同音色之间的定量关系.那么怎样精确地描述音色呢?这就牵涉到大学里面,通信以及相关专业的一门重要专业基础课"信号分析"的内容了.前面不少跟贴提到的"音色由频谱决定","不同频率的信号的组合形成了音色"等等(这些说法都是对的),其概念就来源于信号分析理论里的"傅里叶(Fourier)分析".

"信号分析"理论的一个基本方法,是把各种复杂的波形(信号),统统化为某几种简单信号的叠加.傅里叶分析就专门用来把周期性的复杂信号表达为简单的正弦波信号的和.例如上面的钢琴小提琴波形,也属于复杂信号,难以用一个简单的有限项的函数表达出来,但是运用傅里叶分析法,它们都可以表达成若干个(严格说是无限多个)正弦波相加的形式,如下:

f=C+f1+f2+f3+f4+......

这个式子被称为傅里叶级数.其中,f指原钢琴或小提琴的波形函数,C是一个常数,f1,f2,f3,...则是一个个简单的正弦波:

f1=A1sin(F1+P1)

f2=A2sin(F2+P2)

f3=A3sin(F3+P3)......

这里面F1,F2,F3...等等是每一个正弦波的频率;P1,P2,P3...是初相位;A1,A2,A3...是各自的振幅.根据原波形的一些数量关系,可以求出每一个F,P和A的值,这样就可以确定函数f了.不同的波形表达为傅里叶级数以后,互相之间的差别只在于A,F,和P的数值不同.

示波器里看到的正弦波波形.

这一段数学描述对某些初中生来说不一定完全理解.但是大致理解以后就可以懂得一些常用术语的含义.例如:

f1,f2,f3...这些正弦波都称为原波形f的"频率分量","频率成份",或叫作"谐波",对音乐来说就是"泛音".前面说了,不同的波形表达为傅理叶级数以后,它们之间的差别只在于后面的频率分量f1,f2,f3...不同,而不同的波形反映不同的音色,所以,现在我们可以"科学地"说了:音色不同是由于声音的"频率成份"不同造成的.或者说是不同的"谐波成份"造成的.还可以说是不同的"频谱"造成的.频谱是什么?就是全部频率分量f1,f2,f3,... 组成的大家庭,总称为"频谱".

还有一些重要的数量关系可以从傅里叶级数里看出来.如:

第一个频率分量f1=A1sin(F1+P1),它的频率F1一定是等于原波形的重复频率的.就是上面钢琴波形里的"锯齿"的重复频率,或小提琴里的那个"五峰丘"的重复频率.所以,f1被叫作"基波"或"一次谐波".而后面的各个分量的频率,F1,F2,F3...等,一定是F1的整倍数.如果是两倍,就叫做"二次谐波",三倍则是"三次谐波"...等等.

还有,从傅里叶级数里可以看出来,每一个复杂波形实际上都含有很多个"频率成份",严格说是无穷多个(傅里叶级数是无穷级数),因此,在这个信号传输的过程中,你要是漏掉了其中一部分,那么还原的时候(如喇叭放音时),信号就跟原来的不太一样了,就是音色产生了"失真".失真的一个最重要来源,就在这里.

可是,...可是世界上哪有可以传送无限宽频带的信道呢?所以,...嘿嘿,所以!所有的用喇叭放出来的音乐都是失真的.这就是为什么很多人愿意花大钱买票进戏园子听歌听曲,而不拿三块钱一张的CD替代的原因.懂了一点傅里叶分析,我们就知道这其中的道理了.

好在失真的问题还不是不可逾越的大难题,因为我们还可以从傅里叶级数里看出其它一些东西.其中一个就是谐波的幅度,即A1,A2,A3...的大小,一定是越到后面越小的.A2小于A1,A3又小于A2,...这样到了高次谐波,幅度事实上已很小了.例如8次谐波幅度可能只有一次谐波的几十几百分之一,小到这个程度,有它无它耳朵不一定能够听得出来,那么就干脆丢掉它,当然也丢掉8次以上的谐波成份,只剩下前面的,这样一般听听也就可以了.对耳朵特别灵敏的人,那就用更加高保真的设备,多留一点谐波,让失真更小一点.现在的录音还音设备,不管是磁带,CD还是数码录音,都是这么么干的.可以满足不同层次的需要,这也是CD,磁带和唱片能卖得掉的原因.

还有,......呵呵,扯远了,像在上课了,还是打住.本人只是想尝试一下让初中生懂一点音色和频谱的概念,还不知道能不能奏效,扯多了就是假充老师过干瘾了.

至于月色MM问题的另一方面,不同音色产生的物理原因.这个好解释.声音就是物体震动产生的波,那么,不同的物体震动方式不一样,当然发出的音色也不相同了.包括物体的材质,形状,打击的方向,力度;打击物的大小,硬度,打击速度等等,都会对音色产生影响,这个不难理解.一把音色圆润的提琴,你把琴身上砸个裂缝,声音马上就哑了,这是因为裂缝中有了摩擦,共鸣腔也被破坏,谐振方式变了,音色当然不同了.这时你去看它的波形,一定会出现许多高频率的尖锐的峰."哑"而刺耳的杂音,就来源于此.

胡说八道一通,不对的地方请砸砖.

• 生命、生活精品帖：
• 音色可不仅仅由泛音决定。建议你看看我早年的帖子
• 【提问】从音色想到图象压缩
• 是这个帖子：
• 没有实质内容，恕我不再回复你了，行吗？