主题:真正的难题,纷争的根源 -- 给我打钱87405
以一道数学题为例,来讲解数学的两种风格迥异的思维方式
甲乙二人上午8时同时从东村骑车到西村去,甲每小时比乙快6千米。中午12时甲到西村后立即返回东村,在距西村15千米处遇到乙。求东西两村相距多少千米?
第一种
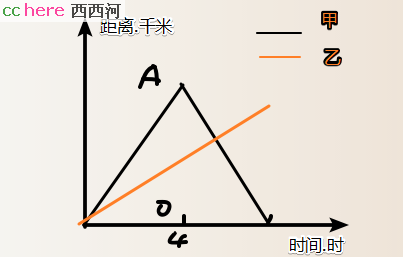
东西两村的距离就是图中AO线段的长度。怎么求呢?
根据题意,AC=4*6=24,ED=15*2=30
所以BC:BD=24:30=4:5
OC:FD=4:5
设OC=4x,有
4x+24=5x+15
解得x=9
AO=4x+24=60
第二种解法:
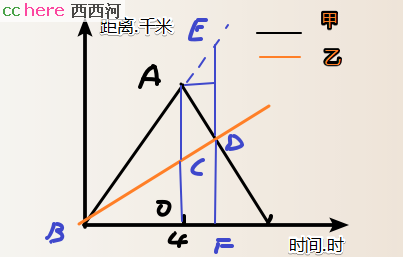
依题意,
AD=4*6=24,指4小时距离差就是速度差乘以时间,即甲抵达D点(西村)时,乙在A点,AD=24km。
BD=15km
所以AB=9km
至此,已将原题转换为:
乙从A地出发,甲从D地出发,二人相向而行,在B点相遇。已知甲比乙快,速度差为6千米每小时,AD=24km,BD=15km。求甲、乙速度。
所以甲速:乙速=甲程:乙程=15:9
甲速-乙速=6千米每小时
故二人出发后1小时相遇。甲速为15千米每小时。
东西村相距15*4=60千米。
此外,还可以将甲从西村返回视为继续沿原方向行进到E点,此时乙抵达B点。显然BE=2BD=30千米
所以之前二人路程差为24千米,现在路程差为30千米,故甲从D到E的用时为1小时。后略。
对比一下这两种思维方式,不难发现其中差异是巨大的。
前一种,有明显的两个阶段,第一个阶段不妨叫“列关系式”,这里是用图来表述,本质和用关系式表述一样。第二个阶段不妨叫“解关系式”,用的是“关系式变形”等相关技巧,在这里是用几何知识解决。
第一阶段与第二阶段有巨大的“鸿沟”。
后一种,其方法是将一个复杂问题进行转换,转换成一个简单问题。
如果要简单的说,前一种,有两个关键词,先“找”后“算”。
后一种,一个关键词,会“想”。
这恰好就是东西方文化的差异所在。
前一种,有浓厚的西方色彩,在解决问题时,仿佛感觉是采集原材料,然后送进工厂加工,最后得到成品。
后一种呢?得像东方人那样,焚香,静坐,冥思,悟道。
其实这道题是一道奥数题,并不会出现在常规课堂中。
中国人为什么这么喜欢奥数题?因为中国人是中国人啊。
抛开这些问题不谈,以数学论,我们会发现,这两种思维都不可缺。
譬如许多解析几何题,在有些情况下,用纯代数解决效率高,在另一些情况下,用纯几何就可以完成,还有一种情况,就需要一半几何一半代数。
回到本题。
第一种解法中,在第二阶段,根本就不再使用“速度差”这个已知条件了。
而在第二种解法中,“速度差”是个核心 条件,从头到尾都在用它。
从这里也会能体会到,西方文化中的“分”,与东方文化中的“合”之不同。我们是怎么“合”的,他们是怎么“分”的,各有“窍门”。
- 相关回复 上下关系8
🙂真正的难题,纷争的根源 12 给我打钱87405 字2025 2018-01-12 10:24:16
🙂人类思想极简史 2 给我打钱87405 字2494 2018-02-08 12:33:48
🙂分合之别

🙂以人类学理论的流变为例,来看人类思想的发展规律 5 给我打钱87405 字6226 2018-02-09 00:05:06
🙂也许应该加上摩尔根,进化一派的开创者 1 桥上 字0 2018-02-09 01:20:53
🙂是……简述,简述 1 给我打钱87405 字0 2018-02-09 01:27:18
🙂悲剧还是惨剧? 6 给我打钱87405 字4245 2018-02-04 09:05:31
😜不可测就别测 1 懒厨 字144 2018-02-04 11:08:51