- 近期网站停站换新具体说明
- 按以上说明时间,延期一周至网站时间26-27左右。具体实施前两天会在此提前通知具体实施时间
主题:横跳没有出路 -- 给我打钱87405
(1)
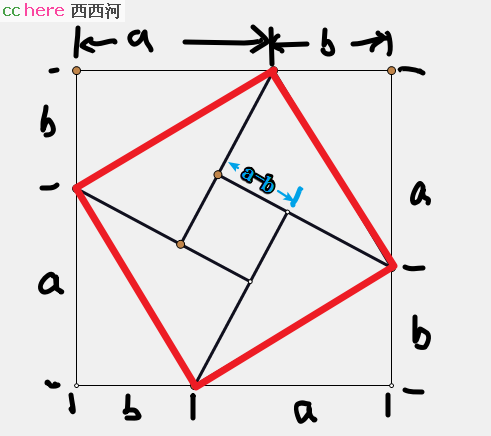
将一个正方形沿红线向内折,就能得到一个内接正方形,里面还有一个小正方形。
然后需要做什么呢?【列出数量关系式】。
学生需要掌握的是:有几个量,能列几个式。
这里有很多量,但例子中只讲面积,有4个量,所以至少能列出4个关系式。如同一个未知数对应一个关系式。
这个,是很多学生没有学会的。
没有学会,就会有很大的麻烦。因为上述内容是【指导思想】,它的功能是“引路”。
往下走。
一共有4个(面积)量,大、中、小正方形的面积,再加所有直角三角形的面积之和,我们给它们分别命名:
S1——大正方形面积
S2——中正方形面积
S3——小正方形面积
S4——8个直角三角形面积之和
于是有:
S1=S2+1/2*S4……①
S2=S3+1/2*S4……②
S1=S3+S4 ……③
以上皆目测可得。
如果没有前述的指导思想,也就能列出这么多。但如果有,那就不一样,学生会【知道】,“还差一个”,因为至少有四个关系式。并且还能猜出来第四个长啥样:①式中没有S3,②式中没有S1,③式中没有S2,所以第四个式子,应该没有S4。
那第四个式子是什么呢?
S1+S3=2*S2
这个关系式是我们目测不出来的。
当然,可能会有人说:S1-S2=S2-S3,怎么说目测不出来呢?对此,我会说:那是事后诸葛亮。人家告诉你了,你必然恍然大悟。
要不然,为什么 勾股定理那么晚才出现?
不入这个门,数学永远学不会,或者永远会觉得数学难。哪一门,都是如此。入门,就是找到了指导思想,有了引路人。
继续。列了四个式子,如果学生认识 不到,这全是加减法,因为都是面积,那不算入了门。因为认识到了这一点,就可以将四个式子转换成下面这个样子:
(a+b)^2=a^2+b^2+2ab
a^2+b^2=(a-b)^2+2ab
(a+b)^2=(a-b)^2+4ab
(a+b)^2+(a-b)^2=2(a^2+b^2)
以上,熟悉不熟悉?多少初中生天天练这个,完全平方式、平方差、勾股定理?
再继续,从中提炼出“要素”:
a+b、ab、a-b、a^2+b^2
前面两个熟悉不熟悉?韦达定理,又联上二次函数跟二次方程了。
韦达定理只不过把下面这句话倒过来说了一遍:
已知一矩形的半周和面积,求各边有多长。
整个初中的所谓“大难点”,有15分钟就搞通了。
为什么 难?脑中木有指导思想,心里没有引路人。用粗暴的话来说,就是:没谱。
5000年前的人类就已经 搞清楚了上述内容,后面只是在“证明”,因为涉及到了负数、无理数……换言之,初中,在学5000年前人类就已经 掌握 的知识,再加一点后期的“延伸”。
(2)
数学入门(2)
为什么同一个节目(比如某个京剧段子),会有人反复的看?
上面讲到,其实韦达定理只是把一个数学问题倒过来讲了一遍。这里面还有文章。
所谓韦达定理,就是指,若ax^2+bx+c=0这样的一元 二次方程有两个实数根x1和x2,那么:
x1+x2=-b/a
x1*x2=c/a
而倒过来 说,则是:
若已知一个矩形的半周和面积,求它的两边各有多长?
设一边长为x,一边长为y,有
x+y=m(半周)
xy=n(面积)
两式消元联解,就能得到一个一元二次方程
x^2-mx+n=0
下面出现了重点:
上述式子,两根必为正数,但是,有可能是无理数根,也有可能解不出来,即,负数开平方问题,也就是后来的虚数根。
大家注意到了吗?
一下就冒了三个概念:无理数、负数、虚数。
然而,对于当时的人来说,他们看到的是什么呢?同样类型的方程,有的能解出来(整数或分数根),有的表达不出来(不会表达无理数),有的【猜出来有两个根,但完全不知道该如何表达它】。
我们中国古代数学是没有负数概念的,我们用的是“借”这个概念。我们的数学之所以没有像西方人那样建立起一个关于数的体系,恐怕不会有第二个原因。
所以我们要问:为什么 无理数、负数、虚数这三个概念这很难以建立?
无理数是怎么回事?无理数是一个“实”的数,所谓“实”的数,意思是说它是可测的,在现实中存在的,客观的。
所以发现无理数的难度要低。
负数和虚数,是“虚”的数,它们是一种“过程”数,这很像【功】这个概念,而不是【能】。换言之,负数和虚数是因为计算的需要而出现在数学语言当中的。
今人之所以感受不到它的难度,是因为今 人只不过把前人的发现背了下来。
感受不到它的难度,一定会对数学的学习造成巨大的阻碍。
好好想想,对于人类而言,是很难建立起“过程”数这样的概念的,难道不是?
因为数学的起源是测量,测量的对象就必然是客观存在的。
为什么 连牛顿都否认虚数的存在呢?
很难,非常难。
那么,为什么 我在这一节的一开始,要提到“为什么 有的人会反复去听同一支曲目呢?”
因为,这个世界上最难练的功夫 就是:当收则收,当放则放。
作为事后诸葛亮,有的人会说:数,有“结果 数”跟“过程数”之分,有“实的数”跟“虚的数”之分,这有什么好奇怪的呢?这有什么难以理解的呢?
那为什么 事前不是这样?
所以,【当收则收,当放则放】这一总策略,并没有被多数人接受,当然就谈不上掌握了。其实,这就是我反反复复提到的:得有两条腿。
很多人是拒绝“当收则收,当放则放”这一总策略的。
为什么 ?因为【没有任何人,可以用人类的语言,明确的告诉别人,什么情况下收,什么情况下放】。别人只能说到这里,只能表达出这样一种“意向”。
多数人采取的策略,往往是【全收】或【全放】。
为什么 会这样?因为多数人“算了一笔账”,若全收或全放,顶多吃点亏,合计是赚的,何必费那个脑子呢?
这两天有一则新闻,说的是一个ID为“辣笔小球”的人因侮辱解放军战士而被刑拘。根据我们的经验来看,这样的人,真的是“反动透顶”吗?其实并不是,相反,往往是不知道开玩笑的边界。对吗?
所以,全收或全放的策略是错的,必须要尽可能的学会“该收则收,当放则放”,必须要【自己去找到】“那个分界线”。
回到数学,请看下图:
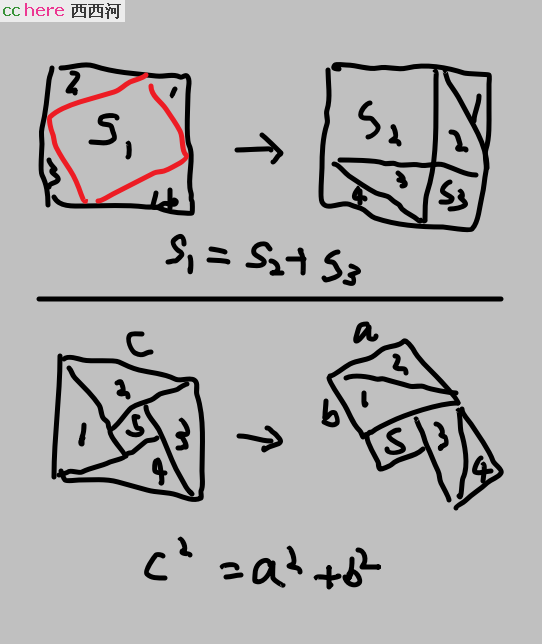
这是发现勾股定理的两条路径。问:哪个难?
这两条路径,各有各的难点:
图中上半部分,采用的策略是“从起始”【直接】跳到“结果 ”,换言之,如果走过程,即将三角形剪下来再重新“拼接”,很难发现勾股定理。
图中下半部分,采用的策略恰好相反,走的是“过程”,即将三角形剪下来,再重组。但是,即便重组出一个新的图形,也很难“看出”勾股定理。
而我们回顾整个数学史,不难发现,数学家恰好也有两大流派,一派是“猜想派”,不知道过程,直接猜 出了结果 ,相当于图中的上半部分;一派是“证明派”,根本没有能力猜结果 ,但非常擅长于一步接一步的推导。
这两大流派往往既有矛盾,又有合作。所谓矛盾,就是“猜想派”提出猜想,“证明派”不予采信;所谓合作,就是“猜想派”提得出猜想,但不会证明,而“证明派”找到了办法将其证明。
为什么 我会经常说,老师不会教?
因为有太多的老师,看不出来学生是哪一块强、哪一块弱,应该在哪里下功夫。更不知道教会学生,解决问题的总策略是【连猜 带证】。
猜想需要什么?天马行空,不受约束。
证明或者说推导需要什么?动作规范,不可以随心所欲。
是不是听起来是相悖的?【不】。恰好相反,这俩是互相合作的关系。
比如前面提到的【有四个量,就必定有对应的四个关系式】,这就是一种规范,掌握 了这种规范,就可以弥补猜想力的不足,通过规范得到一个“想不到的角度”。
而有足够强大的猜想力,就往往可以破题,破了题,才能启动,否则证明力、推导力派不上用场。
下面换一个场景,来谈【当收则收,该放则放】或者说成【两条腿走路】,或者说成【静如处子,动如脱兔】,或者说成【枕戈待旦】。
抗美援朝第一次战役是怎么打赢的?
事后来看,论装备,论人数,论补给,志愿军根本就不是美军的对手。可是为什么 第一次战役“居然”打赢了呢?
关键之战,就是彭德怀命令39军直插美军后方,一举拿下了咽喉要道【云山】。实际上,即便如此,志愿军于“客观”层面来看,仍然不是美军的对手,可是为什么 美军就此溃败了呢?
很简单,打仗不是简单的“拼数据”,打仗是人在打。当美军收到情报,云山被志愿军拿下之后,立刻就陷入了恐慌:“完了!我们被包饺子了”。要说起来,彭德怀乃真战神也。要是林彪来指挥,他是绝不可能下达进攻云山之命令的。因为林彪是典型的“数据党”,在他看来,拿下云山又怎么样?兵力根本不可能围得住美军。既然如此,又何来切断美军退路一说呢?
所以说,对于怎么打仗,林彪是个小学生,根本就没有入门,彭德怀才入了门。他非常清楚,志愿军秘密入朝,美军不知道志愿军到底有多少人,只要将美军后撤路线当中的某个要道拿下,美军必定陷入恐慌,必定自己拔腿就跑,而美军一旦开始“疯了般的后撤”,志愿军的正面部队趁势追击,美军必定会出现陷入混乱,自相踩踏,必定是兵败如山倒。
大伙看,这是不是充分说明了,做人做事,绝不能【全收】或【全放】,而只能【该收则收,当放则放】?
而由于没有任何人可以给出一个量化的指标,教会他人,什么情况下放,什么情况下收,所以练习的重点也只能是不断尝试,不断品味。通过自己尝试,积累相关的经验,通过品味别人的做法和成果,“悟”出点什么来。
- 相关回复 上下关系8
🙂请压抑 给我打钱87405 字0 2021-02-22 21:56:16
🙂那我就压抑。希望您继续,抒发情绪,别憋在心里。 夜如何其 字0 2021-02-22 22:23:04
🙂再干一万年,人类或许就得到了解放 2 给我打钱87405 字2385 2021-02-21 11:58:59
🙂数学入门

🙂总结: 2 给我打钱87405 字1350 2021-02-20 23:45:46
🙂春节期间对我女儿展开了“魔鬼式”训练 61 给我打钱87405 字5400 2021-02-14 04:34:41
🙂我觉得你可以换个思路 2 happyyuppie 字534 2021-02-17 16:39:47
🙂弹一百首完成度百分百的曲子 3 胖儿们的爹 字775 2021-02-17 09:38:13