- 近期网站停站换新具体说明
- 按以上说明时间,延期一周至网站时间26-27左右。具体实施前两天会在此提前通知具体实施时间
主题:【原创】我们学过的数理化——解释潮汐 -- 代码ABC
一个晴朗的夜晚,海边,两父子在沙滩上散步。一轮明月正从东边慢慢升起,同时晚潮也开始涌向沙滩,渐渐磨去父子俩留下脚印。
孩子突然问父亲:“爸爸,爸爸,为什么我们有时把潮水叫做潮汐?汐是什么?”
“潮和汐其实是一回事,都是指海水涨上来,古人说,昼涨称潮,夜涨称汐。你看潮字就是朝(第一声)字加了三点水,而汐就是夕字加三点水。实际上指的都是潮水,不过一次在早上,一次在晚上而已”。父亲微笑着向好奇的儿子解释,同时暗暗庆幸自己对说文解字有那么一手。
“爸爸,爸爸,那么海水为什么会涨起来呢?”
“哦,你看潮水都是随着月亮升起来而涨的,实际上就是月亮对地球海水的吸引力造成的,月亮在我们这边,我们这边的海水就涨起来了。在学校老师不是告诉你们有万有引力这回事吗?这就是引力的一个例子。”,父亲心想好在我这个文科生也知道万有引力。嘿嘿。
“我知道,月亮绕着地球转就是地球吸引着月亮的结果。”
“嗯,聪明。”
“哎!不对!潮水一天有两次,其中一次月亮不在我们这边啊,这是怎么回事呢?”
“........哦,晚上有点凉了,我们回去吧,妈妈在家里等我们呢,对了,你今天的作业做好了吗?我要检查!”
随着孩子逐渐成长,总有超过父亲的时候。难倒父亲的机会将越来越大,不过被简单的日常现象难倒却不是一件值得骄傲的事情,至少不是一件愉快的事。
潮汐的确是由于月亮的引力引起的(实际上太阳的引力也有贡献),不过不是简单的吸引就可以解释。由于地球有一定的体积,因此月亮对地球每一点的引力在大小和方向上都不一样,具体的,在两翼的引力有一个向内的夹角。而靠近月亮那端的引力又比远离月亮那端要大。综合起来这些力除了构成一个向心力之外还在两翼有挤压力,以及在轴线上有拉伸力。这样就产生了潮汐。而且是一次就产生两个高潮和两个低潮。所以潮汐一天有两次。具体的潮汐力计算需要用到非惯性参考系的知识,已经超出了高中物理的要求了。
解释一天为什么有两次潮汐也许真的超过了一个本科毕业文科生的能力,即使是理科生,如果把大学物理当作一门功课来学,也可能在十多年后再次被以前的习题难倒。
有人会说这些知识,孩子迟早也会学到,而且我们学数理化并不是为了在孩子面前炫耀知识。OK,我承认这些理由白分之百正确。实际上除非在专门的研究机构工作,我们学过的大部分数理化知识,在日常也都没什么实际用途。
不过,我真不希望上面的对话在我孩子当父亲或母亲的时候再次重复。也许我们的创造力就在这种得过且过的态度中逐代消磨。所有的发明,发现都是建立在前人的基础上,也就是站在巨人的肩膀上。也许我们不是巨人,但别在巨人的肩膀上滑落。
本帖一共被 4 帖 引用 (帖内工具实现)
你永远解释不清楚的。总会问到你不知道的地方。
这时候的态度应该是鼓励孩子自己找答案,培养自学能力。
惊喜:所有在本帖先送花者得【通宝】一枚
恭喜:你意外获得【西西河通宝】一枚
谢谢:作者意外获得【西西河通宝】一枚
鲜花已经成功送出。
此次送花为【有效送花赞扬,涨乐善、声望】
讲得很好,就是不太直观。特别是那几个力。。。强烈建议配图!
希望楼主能一直把这个系列继续下去 。
其实我觉得这本身就是科学产生与发展的根本驱动力,如果我们脱离了解释这些日常问题的欲望,那么是多么缺乏乐趣的一件事啊。
代码兄高才!让我想起了:
夫君子之行,静以修身,俭以养德。
非淡泊(澹泊)无以明志,非宁静无以致远。
夫学须静也,才须学也。
非学无以广才,非志无以成学。
淫慢则不能励精,险躁则不能冶性。
年与时驰,意与日去,遂成枯落,多不接世,悲守穷庐,将复何及!
有两次在外地的侄女问我初中的数学题,试了试,解不出来,马上google、百度了两下,答案很快就发过去了,搞的小姑娘连声夸我水平高,呵呵。
这段描述我读下来觉得图像还不够清楚,主要因为“两翼”和“轴线”没有对应的解释。我想了一下,自己的理解是这样的:地球月亮之间连条线,海平面可以想象成为是一个椭圆,长轴沿着地月连线。地球和月亮都绕着地月质心旋转,向心力由引力提供。这条线和地球表面相交的两头都会出现(相对)的高潮,靠近月亮一端是因为月亮的引力大于地球表面海水绕地月质心转所需要向心力,所以把海平面“拉”向月亮;远离月亮那端则是因为月球提供引力不足以满足向心力,所以把那头的海平面沿着地月连线往外“甩”,也高了。
高中物理时留下的问题被此贴勾起了。
万有引力公式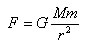
牛顿第二定律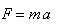
两个球,一个蓝球,一个地球。 放开蓝球,不及阻力篮球以重力加速度奔向地球。篮球受到地球的引力由万有引力公式得到,或者简单点用重力常数。以上很普通,是以地球为参照系-- 一个不大的力使篮球以一个一定的加速度向地球移动。
但是以篮球为参照系,问题来了。 以篮球参照系,地球也是以一样的加速度向篮球移动,并且两者间的力也是一样的一个不大的力。但是我们会发现,当以篮球为参照系时,一个不大的力竟然推动地球这么一个庞然大物以一个同样的加速度向篮球靠拢! 而如果根据牛顿第二定律 F = m * a, 这个力要大的多。
用篮球做的参照系不是惯性参照系,它是由加速运动的,非惯性参照系下所有的其他物体都会受到一个所谓的"惯性力",所以没错地球这时候看上去受到一个很大的力,不过这个力是真实引力和惯性力之和。而且这个力是有真实效果的(物理定律保持不变)!
感觉上很别扭,举一个熟悉的例子——失重,你自由下落或宇航员在轨道上无动力飞行并不是不存在引力而是这时以自己为参照系时引力被惯性力抵消。以地球为参照系时就看不到失重的现象了。
其实地球也不是惯性系,让炮弹跑偏,形成地球上几大风带,让填补低压的气流形成旋转的台风。都是自转的非惯性系里的科氏力起作用。
地球因为质量大,所以加速度很小,考虑篮球的加速的时候可以大致当成惯性系。
反过来,篮球的加速度太大,考虑地球的加速度的时候就不能当成惯性系了。
失重的“惯性力”是同运动状态改变的方向相反的,轨道上是向外、自由落体是向上。
以篮球为参照系的地球,要产生“叠加”而不是“抵消”的“惯性力”,那么其方向必然是朝着篮球方向,是同运动状态改变方向相同的,而不是相反的(由相对静止到朝着篮球运动,要抵抗这种改变,“惯性力”应该是背向篮球的)。
网上搜索了一下,还有更多质疑。
以地球为参照系:由于地球近似为惯性系,所以小物体做自由落体运动,到达地面过程中动能不断增加,其动能是由势能转换而来的,能量守恒成立。
以小物体为参照系:小物体是非惯性系,按照广义相对论,其中有一个附加引力场,引力场指向上。地球在附加引力场作用下,沿着附加引力场方向加速运动,附加引力场对地球做功,地球的动能不断增加,直至落到作为参照系的小物体上。作用于地球的附加引力场使地球动能增加,附加引力场的能量来自何方,用能量守恒怎样解释?
对于以垂直向上发射的火箭为参照系也有同样的问题。
如果自由落体是一种特殊情况,没有附加场。
那么,如果以水平加速的车作为参照系,就应该有附加场了。那么可以观察到地球在向后加速运动,在这个参照系中,地球的动能增量是由什么能源转化而来的呢?
当然以地球为参照系的时候,车的动能增量是由发动机供给的。
全文在这 非惯性参照系附加引力场
貌似广义相对论有解?渴望清晰的图像。。。
关于“惯性力”的方向一事,想了一下,难不成其方向还与物体大小有关?