- 近期网站停站换新具体说明
- 按以上说明时间,延期一周至网站时间26-27左右。具体实施前两天会在此提前通知具体实施时间
主题:【原创】 我所知道的量子力学-量子的起源(二) -- 代码ABC
科学就是这样发展的:提出假设、推导出理论、实验直到假设被推翻,然后重新假设。有些假设看起来很合理但是很快就被推翻,而有些假设看起来很荒谬,却一直无法推翻。于是这些假设就成为构成我们知识体系中的一部分。在二十世纪初,物理体系出现了两个很违反直觉的(荒谬的)的假设,其中一个建立了相对论,另一个就是普朗克的假设,发展成了量子力学。两者同时把经典物理体系翻了个底朝天。
我记得在中学课本上是这样讲述普朗克揭开量子秘密的一角的:普朗克推导出正确的黑体辐射公式之后,发现只能假设能量是一份一份地辐射和接收才能解释这个公式。不少科普文章也是这样介绍的,甚至还有反过来的说法,即普朗克假设能量是一份一份地辐射和接收才推导出正确的黑体辐射公式,不过后一种说法不符合历史事实。
就我个人的看法爱因斯坦的假设还好理解,而普朗克的假设到现在都很模糊,因为从这个基础上发展出来的量子力学不断地推翻我们的直觉经验,甚至试图改变我们的世界观!
不管怎么样,我一直很好奇普朗克为什么要做这种假设。而在普朗克之前其他科学家是怎么假设的。
而所有这些事情是从一个公式开始——黑体辐射的能谱公式。具体来说就是黑体在给定温度下,其辐射能量随波长(频率)的分布。
物体辐射能谱的研究起源于天文学家对太阳辐射的研究,1859年德国物理学家基尔霍夫发现了一个这样的规律,即物体在相同温度、相同波长下的辐射能力和吸收能力成正比,这个比例和物体的构成、形状等其他物理特征无关!只和温度和波长有关。也就是这个比例是波长和温度的函数。这就是基尔霍夫辐射定律。这个描述对文科生也许很抽象,不过没关系,大家只要记住吸收厉害的东西,辐射也厉害就行了。
举个例子,我们知道深色的东西吸收热量的能力比较强,所以在需要吸热的地方我们会涂上黑色。然而夏天一些呆在家里的老人喜欢穿深色的衣服,难道他们觉得还不够热吗?其实因为深色的衣服吸收好,反过来辐射能力也很强,在室内阴凉的地方人体温度比环境高,辐射是主要的,穿深色衣服反而更容易让身体的热量辐射出去,也更凉快。另外大家留意一下许多散热器也是涂成黑色的,这就是利用黑色更容易辐射热量的本领,和许多人得直觉相反在其他条件不变的情况下,黑色散热器的效率比白色的更高。
回过头来看基尔霍夫的辐射定律,由于这个辐射和吸收的比例和物质无关,因此我们只要找到一种能完全吸收辐射的物体,研究它的辐射就可以得到这个比例。从而方便我们研究其他物体的辐射或吸收本领。物理上我们称这种吸收一切辐射的物体叫“绝对黑体”,而“绝对黑体”的辐射能谱就是这个比例。
如何找到绝对黑体呢,一般的黑色染料是不行的,因为大部分的黑色染料只是吸收可见光,而实验需要吸收所有波长的物体,聪明的科学家使用了一个巧妙的方法:在一个空腔上开一个小洞,这个洞就可以当作是绝对黑体的近似。因为进入小洞的光(或者说辐射、电磁波),要经过多次很巧合的反射才能恰好从洞口出来,这种概率太小了,因此我们可以认为这个小洞吸收了所有的辐射。另外人们还在空腔里面安排了许多迷宫式的反射壁,进去的光线就更难出来了。
基本上,我们可以把许多空腔上的小洞看作是绝对黑体,其辐射谱就是黑体辐射谱。由于辐射谱中能量密度最大的波长和温度有确定的关系(这个关系很早就被找出来了),因此我们可以用它来测量一些难以直接测量的温度,如炼钢炉里面的钢水温度。只要在炉上开一个小的观察窗(绝对黑体),测量从这个窗口辐射出来的光谱就可以知道炉膛的温度。同样的方法也可以帮助天文学家测量遥远的恒星的表面温度(这种方法测得的温度叫等效温度,并不是实际温度)
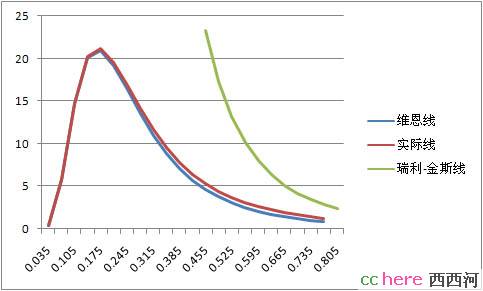
经过测量,人们得到了黑体辐射的能谱分布。如图中的红色线。然后科学家们开始提出各种假设,试图推导出和这条谱线一致的公式。历史上有两条著名的公式:维恩公式和瑞利-金斯公式,分别对应途中的蓝线和绿线。分别代表着人类对辐射机制的两次解释的尝试。很明显都是失败的。也就是这两个假设都是错误的。
我要再去翻书本了,待续......
本帖一共被 2 帖 引用 (帖内工具实现)
不过翻书的时间不能太长,不然新内容来了,以前的内容忘记了还得复习,我这人比较懒,嘿嘿。
送花还居然得宝,好久没有得宝了,谢谢。
鲜花已经成功送出。
此次送花为【有效送花赞扬,涨乐善、声望】
your piece is a good one, now about 白,黑
1. 白光, well explained
"王季烈(1873—1952)清末民初物理学著作翻译家:
季烈并不是单纯做文字工作,而是在融会贯通之后加入了自己的见解。如在中册第三编“光学”的第二章第八节“薄片的色彩”中,先说明透明薄片的干涉色,然后为了解释厚片上不能呈现干涉现象的原因,他设计了一个表示光波长与光程差关系的图解并辅以文字说明。他指出白光的各单色成分中不是单一波长,而是比较接近的波长的集合,每一色光内各波长的干涉图在光程差累积得较大后在互相叠加时已经明暗抵消,各种色光再作叠加就更显调匀,呈现白色了。这样考察各色光的有限的相干性,比笼统地说各色光的干涉图叠加即显白光更为精确、合理。"
2. what about 黑? and
"为什么黑色会吸收光而白色反射光?"
3. 各色光的干涉图叠加即显白光, 中央極限定理
“常態分布在十九世紀後半所受到的推崇,可用英國生物統計學家Galton(1822~1911年)的一段話為代表:「一片混亂中的秩序──我沒見過任何事情像『誤差機率定律』這種絕妙形式的宇宙秩序,那麼容易激起人類的想像力。假如希臘人知道這樣的定律,他們一定會把它擬人化、神格化。它帶著安詳與極度的謙退,君臨著極端的混亂。暴民愈多,無政府狀態愈明顯,愈發顯得它的威力。它是無理性世界中的最高法律。」“
http://www.cchere.net/article/1704845
“觀測是一件重要的科學活動,然而再怎麼小心謹慎,同一對象的兩次觀測總是難免有所出入。科學革命之後,觀測的活動愈來愈多,尤其在天文方面,於是科學家就因重視觀測所得之值與「真」值之間的差異,而開始研究誤差理論。雖然早些就有些人認為誤差的分布與常態分布有關,但1809年Gauss(1777~1855年)提出觀測誤差的常態分布理論後,常態分布才隨Gauss的名聲而引人注意。因此常態分布又稱為Gauss分布。
1812年Laplace(1749~1827年)證明了中央極限定理(central limit theorem)。這個定理大致是說:假定有數目相當多的、互相獨立的變量,這些變量的機率分布雖然可以不同,但它們的標準差的大小相若,則這些變量的和的機率分布大致是常態的。“http://www.cchere.net/article/1704845
“中央極限定理也可以用來解釋誤差的分布。觀測的誤差可以看成是由許多小的、人所無法控制的因素造成的。這些因素可能是天氣的變化、視覺的差異等等,而它們又可能分成更多更細小的因素。假定沒有一個影響性很強的因素,則每個因素都只會引起觀測的小誤差,而其和就是觀測的總誤差。所以根據中央極限定理,“
绿色线和实际线差的太远是显而易见的,但蓝线和红线差的并不多啊,为什么说维恩公式错了呢?
zt
黑白分明
“黑白分明!”我们无数次地听人们这样形容那些非常简单、一眼就能看得清清楚楚的事情。正因为黑白的反差如此明显,你或许会认为,要搞清楚我们如何分辨黑白两色,肯定易如反掌。
但如果你真的这么想,那就大错特错了。眼睛感知这两种完全相反的色彩似乎不费吹灰之力,但这种表面上的轻松掩盖了一项有关视觉的基本事实:每当我们盯住一处地方,想要看个究竟时,我们的大脑实际上都是在执行一项非常艰巨的任务。举个例子来说,在相同的光照条件下,白色表面反射的光,当然比黑色表面多得多;但另一方面,阴影下的白色表面反射的光,却可能比阳光下的黑色表面反射的光更少。然而,我们肯定不会因此便指黑为白或指白为黑,总能准确无误地明辨黑白。显然,大脑肯定在依靠某种程序来解读这类环境信息——对于像我这样的神经科学家来说,这种程序可谓神秘莫测。
对于我们如何分清黑白这个问题,科学家进行了长期的考察。这方面的最新研究成果有助于我们深入了解人的视觉系统,了解它如何正确地分析进入眼睛的光线模式,并根据它来推断物体的颜色。
除了使我们对人类大脑的运作机制有更加全面的认识外,这类研究工作还可以帮助我们设计机器人使用的人工视觉系统。对人类来说,许多模式识别问题完全是小菜一碟,但电脑在应付这类问题时的表现却纯属白痴水平,这早已是众所周知的事实。如果能设法让电脑“看清”东西,那它就能为我们做更多的事情了:电脑控制的无钥门锁可以识别出主人的面孔,自动为主人开门;电脑操控的汽车可以带着我们满城跑,既快捷又安全;在家里,电脑可以为我们送上报纸或者收拾房间的垃圾。
同大脑过招
研究视觉的科学家们依靠所谓的“精神物理学”方法,软硬兼施,逼迫大脑“吐”出隐藏的秘密——当然,大脑不会像竹筒倒豆子一样,老老实实地和盘托出它的底细。事实上,这个过程有点像所谓的“二十题游戏”[game of 20 questions,源自美国动画片《星球大战》中的任务达思·韦德(Darth Vader)。游戏中的一方向另一方提出20个问题,根据对方的回答猜出他现在正在想什么]。我们向大脑提出一些问题,大脑只会用“是”或者“不是”来回答我们,我们再据此推断大脑的动作机制。为了得到一个明确的答案,从至少两种相互对立的理论假说中挑出更加正确的那种,我们必须周密地设计一套测试图案,图案中必须包含这样一个“目标”表面:根据不同的理论假说,它在大脑中呈现出来的样子会各有不同。比方说,如果其中一种假说成立,这个表面将呈浅灰色;如果是另一种假设成立,它将呈深灰色。在判断那些理论假说孰是孰非的过程中,这样的“目标”表面会起到关键作用。这些测试常常会令我们产生各种有趣的视错觉,这一点我们在下面将会看到。
认出某个表面是黑色、白色还是灰色,看似轻而易举,却包含了一个相当复杂的过程。为了充分认它的复杂性,我们不妨回顾一下某些基本的物理原理。白色表面可以把照射到它上面的大部分光反射回去(反射光占到了入射光的90%左右),而黑色表面只能反射大约3%的入射光。反射光线进入眼睛的瞳孔后,晶状体便将光线聚焦到眼睛后部的内表面,即视网膜上。这就像光线透过镜头进入照相机后,聚焦在胶卷上一样。视网膜中的光感受器可以测定到达视网膜的入射光量。
这么说来,事情岂不是很简单吗?我们暂时还不敢这样断言。当我们盯着某个物体时,从物体表面反射的光其实并不包含任何有关表面灰度的信息。正是由于这个微妙的原因,大脑如何识别灰度的问题才特别受关注。
在任何一个场景中,进入眼睛的总光量主要取决于场景的照明程度,其中特定物体的表面反光率(即表面反射光在入射光中所占的比例)起到的作用则要微弱得多。在同样的光照条件下,白色表面反射的光比黑色表面反射的光多30倍左右。但是,在明亮的阳光和皎洁的月光下,同一个白色表面反射的光可以相差数百万倍。事实上,强光照射下的黑色表面反射的光,轻轻松松就可以超过阴暗处的白色表面反射的光。由于这个原因,现在的机器人还无法识别视野内物体的灰度等级,只能测量某一个指定物体反射的光量(即亮度)。但现在,我们已经知道亮度高低与物体表面是黑是白并没有必然的联系,任何一个表面都可以呈现出任意高低的亮度。
美国心理学家汉斯·沃勒克(Hans Wallach,1904年-1998年)在意识到物体的反光本身无法提供足够的信息让大脑辨别黑白后,于1948年提出了这样的猜想:大脑通过比较眼睛从邻近表面接收的光,来判断一个表面的灰度。沃勒克是爱因斯坦的表弟,长期任职于美国宾夕法尼亚州的斯沃思莫尔学院。他的一系列研究对当代视觉与听觉感知理论具有重大贡献。他通过试验演示证明,把一块色彩均匀的单色纸板放在受试者面前,只须适当改变纸板周围光的亮度,就可以使受试者觉得这块纸板呈现出由黑到白的任何一种色深,而事实上,纸板本身并没有发生任何变化。
下面,让我们来看看一种典型的错觉。测试图案上一个灰色方框被放在纯白的底色上,旁边则是一个完全相同的灰色方框,被放在纯黑的底色上。如果人眼感觉到的颜色深浅完全取决于眼睛接收到的光量,这两个方块看起来就应该一模一样,毫无区别。可事实上,你会发现黑底上的方块颜色好像要浅一些,这就说明大脑在判断颜色深浅时,会与相邻的表面进行比较。
还有一些较新的证据表明,这种与相邻表面的比较甚至比沃勒克当初想象的更简单。看来,眼睛判断颜色深浅的第一步,并不是测量场景中每一个点的光线强度,而仅仅是测量场景中每一条边界处的亮度变化。
沃勒克的研究成果表明,两个表面的相对亮度是解读视觉感受这个难题的重要环节。但是,如果我们只知道相对亮度,那么,对于判断颜色深浅来说,依然存在相当大的不确定空间。如果遇到另外一种情况,场景中某个区域的亮度是邻近区域亮度的5倍,那单凭这一点,眼睛会作出什么判断?它可以判断其中一个区域为灰色,另一个区域为黑色,同样也可以判断两个区域为白色和灰色。因此,相对亮度本身只能告诉你两种色深间的差别有多大,而不能告诉你每一种色深的具体深浅。为了确定某一个表面的确切灰度,大脑需要知道更多的信息。也就是说,大脑需要一个可供比较的基准点,以此来确定不同的色深。现在,研究人员称它为“锚定规则”(anchoring rule)。
目前,有两种不同的锚定规则。沃勒克本人和“即拍即得”照相术的发明人埃德温·兰德(Edwin Land)提出的锚定规则是,场景中亮度最高的色彩被眼睛自动感受为白色。如果这个规则成立的话,那么,它就定出了一条标准,大脑可以用它来对其他所有较低亮度的色深进行比较判断。另外一条锚定规则是心理学家哈里·赫尔森(Harry Helson)在20世纪40年代提出的所谓“适应水准”理论。这个理论认为,某个场景的平均亮度总是被视为中等灰度,然后,大脑只需要把其他各种亮度的色深与这个中等灰度值进行比较,便可以确定或深或浅的各种灰度了。机器视觉领域的研究人员把这个规则称为“灰色世界假设”。
最大亮度理论与灰色世界理论,哪种说法正确呢?1994年,在我的实验室中,研究人员决心要把这个问题弄个水落石出。我和同事们一起,在美国新泽西州立大学设计了一种相当巧妙的办法,可以检验上面两种假设是否正确。实验所需的条件极其简单:只需要两个可以充满受试者整个视野的灰色表面即可。我们要求自愿参加试验的受试者把头伸进一个硕大的不透明半球中,半球内表面的左边涂成中等深度的灰色,右边则涂成了黑色。我们把这个半球悬挂在一个更大的矩形柜子中,柜内的灯光为受试者提供一种漫射照明的效果。
记住,大脑现在对半球内表面上这两种灰度的色深究竟有多深还一无所知——它只知道两者的相对亮度。如果大脑的锚定规则是基于最大亮度理论的话,涂成中等深度灰色的那一半就应该呈现为白色,而黑色的另一半则应该呈现为中等灰色。但如果大脑的锚定规则服从平均亮度的话,中等灰度的那一半就应该是浅灰色,而涂成黑色的那一半则应该是深灰色。无论哪一半,都不会被受试者看成黑色或白色。
实验结果一清二楚,在受试者看来,中等灰度的那一半是彻头彻尾的白色,而黑色的那一半则呈现为中灰色。因此,我们感觉到的灰度标尺是被锚定在“顶端”,也就是最高亮度,而不是平均亮度上的。这个结果大大加深了我们对于“大脑如何计算简单场景中的灰度”这个问题的认识。在受试者眼中,亮度最高的表面呈现为白色,而深色表面的灰度则取决于它的亮度与场景中的最高亮度之差(更确切地说,是取决于这两个亮度之比)。
错定标准变变变
我们在日常生活中遇到的场景,要比上述实验中的理想场景不知道复杂多少倍。那么,在现实中,情况又如何呢?上面那种简单的理论行得通吗?此时,如果得知这个问题的答案是“行不通,现实情况要复杂得多”,读者们大概也不会觉得意外。如果大脑只是把每一个表面的亮度同整个场景中的最大亮度作比较的话,那么,明亮光线照射下的黑色表面与阴影下的白色相比,可能具有相同的亮度(而事实上,也的确常常出现这种情况),因此在观测者看来,它们呈现出的灰度应该是相同的。然而,实际情况并不是这样,我们能够看出两者的差别。由此看来,视觉系统必定在不同的照明区域内,运用了不同的锚定标准。
事实上,许多对视错觉进行的研究也证明,锚定标准的确会发生变化。如果我们把几个一模一样的灰色圆形纸片,粘贴到一张有许多明暗区域的照片上,那么,贴在阴暗区域上的纸片灰度,看起来就会比明亮区域上的纸片浅得多。我把它们称为“试探纸片”,因为我们可以用它来探测视觉系统如何在场景中的不同位置计算灰度。在任何一个给定的照明区域内部,纸片的实际位置并不重要:无论你把它贴在哪里,纸片灰色的深浅看起来都大致相同。
从功能上说,每一个照明区域似乎都有自己的锚定标准。也就是说,大脑把具有某种亮度的表面视为白色,并以此为基准,来判定这个区域内其他表面的颜色——而且,不同照明区域内的“白色”标准还不一样。然而,如果我们要为机器人编制程序,使它能够用这种方法处理图像的话,我们将面临巨大的挑战。为了把图像划分为若干个具有不同照明度的独立区域,视觉系统必须判定图像中哪些边缘是色深发生改变的地方,而哪些边缘又是照明度发生改变的地方(例如,阴影轮廓形成的线条就属于这一类)。举个例子来说,如果某条边缘模糊不清,或者代表了某个平面上突然出现的转折,比方说拐角,那么,这种视觉判断程序可能就会认为,这是一条区分不同照明区域的分界线。
有些理论研究者——如美国北达科他州立大学的芭芭拉·布拉克斯李(Barbara Blakeslee)和马克·麦康特(Mark McCourt)——认为,人类视觉系统也可以不使用这套边缘分类方法。他们提出了一种更加简单的视觉处理过程,也就是所谓的“空间过滤”。如果把他们的理论运用到我们前面提到的那幅粘贴了灰色圆纸片的照片上,每个纸片的灰度将主要取决于纸片边缘处的局部亮度反差(这与沃勒克此前提出的主张异曲同工)。他们或许会进一步指出,照片中每个纸片表现出的灰度,仅仅取决于纸片与它周围底色之间亮度反差的方向和强度。
如果,我们将若干试探纸片放在一个有一片阴影区域的棋盘状图案上,可以看出,局部反差相同的纸片看起来可以呈现出不同的灰度,而局部反差不同的纸片,表现出来的灰度却有可能相同