- 近期网站停站换新具体说明
- 按以上说明时间,延期一周至网站时间26-27左右。具体实施前两天会在此提前通知具体实施时间
主题:【原创】网络分裂症 [1] -- 邓侃
[1] 链接出处
[2] 链接出处
[3] 链接出处
1894年,发现了电磁波的德国人Heinrich Hertz去世。Hertz去世以后,原本没有发表的实验记录和笔记被整理出版了。当时才20岁的意大利人Guglielmo Marconi读到这些文献的时候,正在阿尔卑斯山上度假。读着读着,Marconi的头脑中,浮现出了利用电磁波来发射和接收无线电报的具体构想。小伙子越想越兴奋,连阿尔卑斯山的美丽风景也顾不上了,急忙跑回家去,着手实现无线电报的发射和接收机。Marconi幼时学习成绩并不好,但是伟大的发明似乎和小学成绩并不特别相关。只用了十来天,他的构想就变成了现实。
起初,无线电报的发射距离只有几百米,但是Marconi觉得只要改进发射机的设计和功率,就可以覆盖更大范围。为此,他开始四处寻找资助,但是四处碰壁。无奈之下,两年后他去英国伦敦碰运气。很快,他的发明受到英国邮电部总工的青睐。此后,他的事业蒸蒸日上,无线电波的覆盖半径也不断扩大,从6公里,到16公里,一直扩大到 3000多公里。
1909年,Marconi获得诺贝尔物理学奖。在颁奖演说中,他谈到如果想在地球表面,人类可居住地区的任何两点之间收发无线电报信号,需要多少个无线信号中继站的问题。根据他的计算,最多只需要5.83个。这就是所谓“六度空间(Six degrees of separation)”的由来。
Marconi的六度空间纯粹是个技术概念,二十年后,匈牙利人Frigyes Karinthy写了一篇小说,题目叫“链接(Chain-links)”。虽然这是一篇文学作品,但是Karinthy在文中提出了一些关于网络的问题,让后世的数学家,物理学家,计算机科学家以及社会学家苦思冥想,至今也没有找到完整的强有力的答案。小说中有一个大胆的猜想,就是六度人际空间。设想有三个人,A认识B,B认识C,但是A不直接认识C,那么从A到C的距离是2。六度人际空间的猜想是,世界上任何两个人之间的距离不超过6。换句话说,无论你想认识世界上任何人,只需要找到5个中间人做介绍就可以如愿以偿。
之所以说这是一个大胆的猜想,是因为它有悖常识。假如从人群中随机挑选100个人,那么其中任意两个人的距离,最短是1,也就是他们相互认识,最长是无穷大,也就是在这两个人之间不存在任何直接的或者间接的人际关系链。即便我们不考虑无穷大的情况,而是强加一个限制条件:在这100个人中,任何两个人之间都可以通过一连串中间人介绍认识。那么在这个限制条件约束的范围内,两个人之间的最长距离是99。从最短距离1,到最长距离99,人与人之间的平均距离应当是多少呢?按照常识推断,很多人以为是50。但是Karinthy却说不对,应当是6甚至更小。尽管听起来荒谬,但是要找到反例来证伪,还真不容易。
Karinthy 的六度人际空间的猜想引起了很大反响,原因不仅仅在于这个猜想不合常理却又似乎成立,更重要的在于它所隐喻的哲学意义。我们人类分散居住在五湖四海,但是作为一个社会群体而言,大家并非散落各处相互隔绝,而是非常紧密地联系在一起。这个说法,对于向往世界大同的人们,实在是一个渴望已久的“科学”依据。
但是,Karinthy的猜想,是不是真得能经受住科学的严格考验呢?从1929年Karinthy的小说问世开始,人们试图通过各种手段,论证这个猜想是否成立。四十年过去了,直到1969年,美国哈佛大学教授Stanley Milgram终于想出了一个比较有说服力的试验办法。他在美国各地随机挑选了296个居民,分别给他们写了一封信,在说明了试验意图以后, Milgram要求他们把这封信寄给某一个不著名的人,我们把他称之为D。如果他们恰好认识D这个人,就直接把信寄给他。但是大多数情况下,他们不认识 D,在这种情况下,Milgram要求他们想一想,他们的朋友中谁最有可能认识D,然后把信转寄给这个朋友,由他代转。Milgram发出了296封这样的信,其中绝大多数信件泥牛入海,但是有64封成功到达终点。在这64封信中,每封信平均经过5.5次转寄。Milgram的试验基本上能证实,任何两个美国人之间的距离不大于6。
Milgram的试验获得了很多人的认同,但是也遭到了一些质疑。人们会问,如果世界上存在某个小岛,小岛上的土著与世隔绝,那么这些土著与我们的距离就是无穷大,6度人际空间不严格成立。有意思的是,世界上的确存在这样的小岛,譬如印度洋上的North Sentinel岛,他们顽强地保持着古风,不与文明世界来往。另外还有人把问号投向中途遗失的232封信。是大家放弃了这个试验呢,还是虽然大家极力想把信件转寄到终点,但是偏偏就是不能如愿以偿?如果是后一种情况,那么美国人之间的平均距离,就有可能远远大于6。
后来的研究者们继续类似的试验,有的通过email方式重复这个试验,有的分析Facebook这样的社交网里的人际关系。得出的结论是,六度人际空间基本是成立的。当然这只是一个统计规律,并不排斥像North Sentinel这样的少数反例。
接下去的问题是,为什么会存在六度人际空间这样的规律呢?
本帖一共被 6 帖 引用 (帖内工具实现)
[1] 链接出处
[2] 链接出处
[3] 链接出处
如果把人际关系看成是一个网络,每个人都是一个节点(node),如果A和B两个人相互认识,那么就存在一条连接节点A和B的边(edge)。人际关系网就是这样一张由节点和边组成的图(graph)。某个节点上的边越多,说明这个人的朋友越多。人与人的社交能力和偏好不同,有的人高朋满座,有的人乐于独处。从整个人类来说,人的社交范围的分布是什么样的呢?换句话说,每个节点上的边的数目,是服从什么样的概率分布呢?
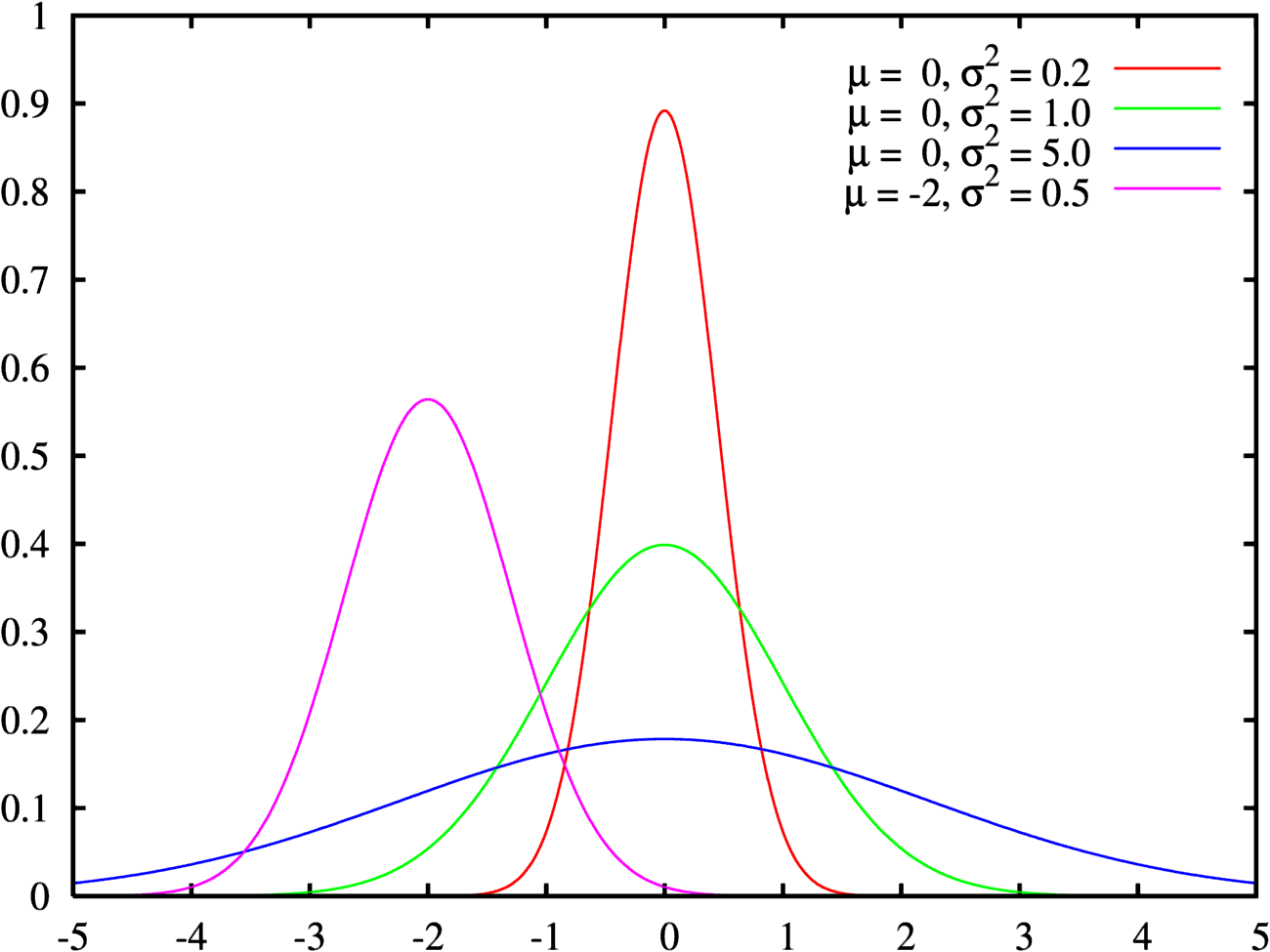
很多人以为是随机分布,就像男人的身高一样,在1.65-1.75米之间的男人很多,1.90米以上的人数少一点,超过2.00米的就更少。随机分布的形状像个倒立的钟,左右对称,如下图所示。很多人认为人类的社交范围也服从正态分布,大多数人平时经常联系的人,为数也就20-30个,少数人特别热衷于社交,他们或许会认识50个甚至更多的人,也有少数人习惯离群索居,他们平时接触的不超过10个人。果真如此吗?
1998年,美国圣母大学的教授Albert-Laszlo Barabasi写了一本书,书名叫“链接,网络的新科学 (Linked,new science of networks)”。这本书里谈到一个观点,认为人类的社交范围应该服从幂次分布,如下图。
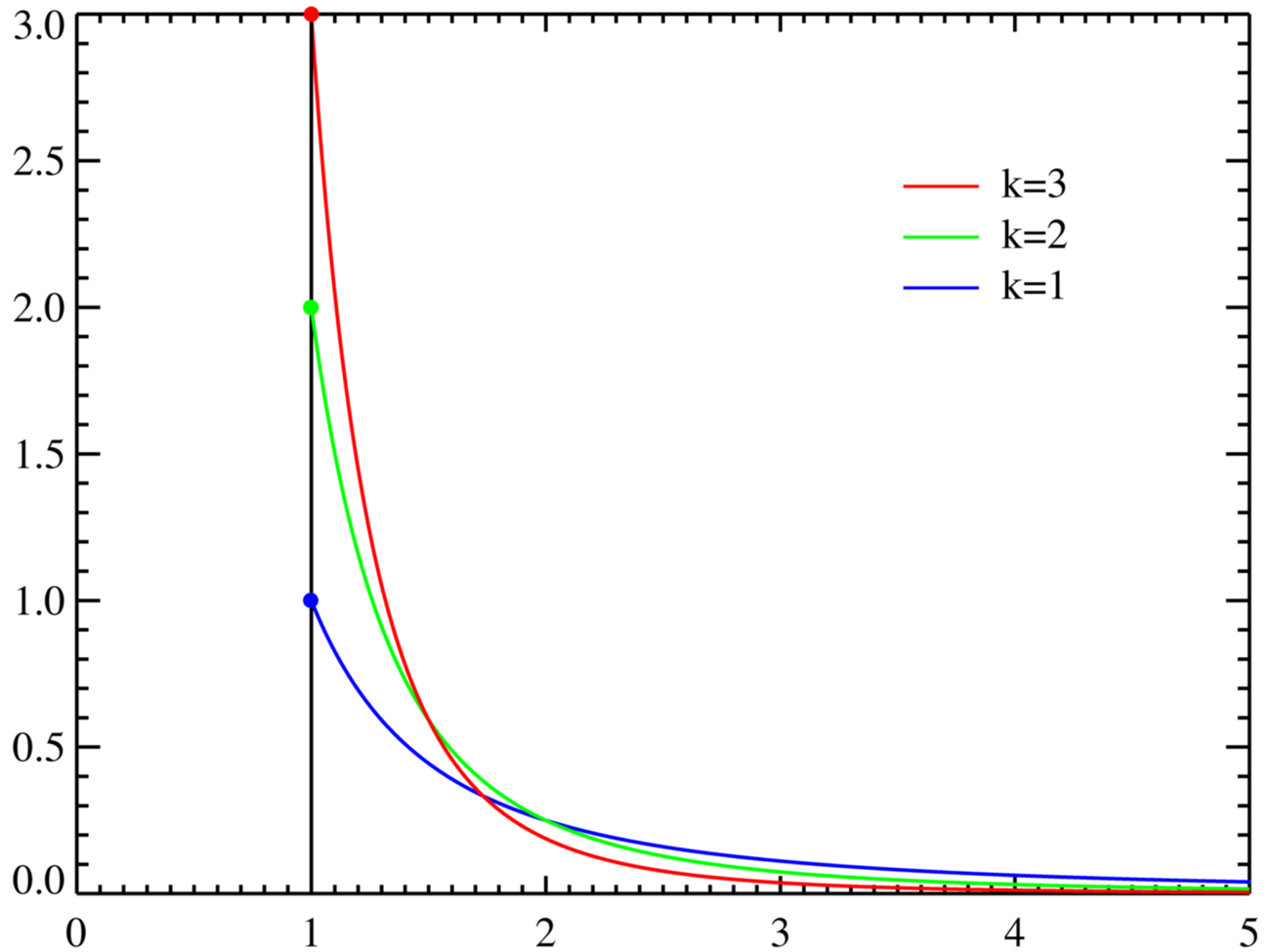
通俗一点讲,20%的人认识很多其他人,他们是人际关系网的中枢(hub),而剩下的80%的人,他们的社交范围非常有限。在这个关于社会主义搜索引擎的文章系列的第一篇,我们曾经谈到过80/20现象,又称为长尾理论。Barabasi把80/20这样的通俗说法量化了,用幂次分布的数学模型,更精确地描述了80/20现象。
Barabasi这个人很有意思,他的专业是理论物理。但是他没有去研究量子力学相对论等等经典的物理课题,而是涉足计算机网络,尤其是他的团队做了一个网络爬虫(web crawler)。做网络爬虫的人很多,譬如Google的两位创始人,他们也做了网络爬虫,在这个基础之上,他们开发了Google搜索引擎。使用同一种工具,生产出的结果却不一样,Barabasi没有用网虫来实现搜索引擎,却用它来研究网络的拓扑结构。
说得详细一点,Barabasi看到的现象是,每个互联网的网页通常会有几个链接,连到其它网页。他感兴趣的问题是,每个网页的链接的数目相互不同,这些数目的分布有没有规律可循?随着互联网的发展,网页的链接也随之变化,变化的趋势是贫富分化加剧还是大家趋同?由此引申出来的问题是,如果我们想创建一个网站,我们应该如何经营才能使它越来越有人气。或者反过来讲,如何打击我们的竞争对手,争夺他们的人气?
Barabasi 的研究发轫于互联网的拓扑结构,但是他没有局限于此。他把类似的思想方法推广到其它领域,包括传染病的传播与控制,公路网与航空线路网,基因与蛋白质的多元因子互动,人际关系网,语义网(Semantic network)等等。他发现这些不同领域的网络,具有类似的特性。他把具有这些共同特性的网络,命名为无标度网络(scale-free network)。
无标度网络有几个显著的特点。第一个特点是,无标度网络的联通,高度依赖于几个中枢(hub)之间的联通。譬如中国和美国,各有几亿国民,但是两国国民的个体之间的联系并不能左右两个国家的整体关系。国与国的关系,掌握在政府,大企业和号召力强的民间团体手中。这个特点可以为我们提供一些行动指南。譬如有人建议通过民间外交来提升中美关系,假如遵循这个指导思想,我们通过奥运会或者世博会,争取了一千个甚至一万个美国草民来我们中国参观,并且成功地吸引他们热爱中国,中美关系会不会因此升温呢?无标度网络理论的结论是不会。反过来,如果我们有办法让CNN立场变得亲中,或者让好莱坞多拍几部像“功夫熊猫” 那样的宣扬中国文化的电影,美国民众就会普遍受其影响,改变对中国的观感。
[1] 链接出处
[2] 链接出处
[3] 链接出处
第二个特点是,随着无标度网络的进化,越来越多的边(edge)向中枢节点(hub node)汇集,形成贫富分化的局面。Barabasi研究了美国的公路网发展史。美国早期只有乡村小路,杂乱无章地连接各个村落。后来有了公路,再后来有了城际和州际高速公路。虽然乡村小路也有很大发展,但是自觉不自觉地,这些乡村小路都与城际和州际高速公路相联通,形成以城际和州际高速公路为主干,以乡村小路向四处蔓延的公路体系。互联网的发展也如此,刚开始的时候,各种网站百花齐放,各领风骚,但是逐渐逐渐,用户向少数几个大网站聚集,形成寡头局面,其它小网站渐渐退出舞台。
第三个特点是围绕中枢与之密切联系的,是次一级中枢,而围绕次一级中枢的,是再次级中枢,形成一个等级结构。譬如新浪网的博客拥有广大的读者群,其中徐静蕾韩寒等人的博客人气极盛。而徐静蕾韩寒他们的朋友的博客,通常也很有人气,而且面向同一个读者群。假如我们也想建一个博客网站,与新浪网争夺人气,无标度网络理论给我们的建议是,争取徐静蕾韩寒来加入我们的网站,如果他们不同意,就争取他们的朋友来加入,因为他们的朋友会把徐静蕾韩寒等人的读者带过来。无标度网络理论把这个特点命名为“偏好连接(preferential attachment)”。
第四个特点叫着"集群系数(clustering coefficient)"。在第三个特点里面,无标度网络理论告诉我们,中枢是分等级的,像是一个金字塔型结构。假如我们的博客网站野心很大,想把徐静蕾韩寒的读者群整个吸引过来。有没有必要花大力气,把整个金字塔从头到脚无一遗漏地统统策反呢?无标度网络理论的结论是不需要。金字塔的底部是一个一个小圈子,每个小圈子里的所有人都相互认识,但是他们与外界的联系相当有限。每个小圈子都有为数不多的少数几个人充当与外界的联络人。所以,只要争取到了这些小圈子的联络人,整个小圈子的意识和行为就会发生变化。
应当指出的是,无标度网络理论目前只是一个设想,还没有得到严格的科学论证和普遍接受,与经典的学术理论也有冲突。譬如,经济学通常有个假设,认为每个人都是理性个体,他们有独立思考的能力,从而他们的意识形态也是独立的和理性的。但是无标度网络理论描绘的却是另一幅图景,以无标度网络为特征的社会人际关系网中,绝大多数草民的意识行为受到精英阶层的左右。从这个意义上讲,中国古代绘画与无标度网络理论倒是一拍即合,因为在中国古代绘画中,没有科学的透视法则,“大人”如达官雅士,通常被画得很大,而“小人”如仆役书童,通常被画得如侏儒一般。
另外,还有一种对无标度网络理论的批评,认为这个所谓理论,只不过是把大家司空见惯的常识,用数学的语言,重新叙述一遍而已,并没有什么实质的新鲜内容。对于这个观点,笔者是不同意的。的确,无标度网络理论总结的几个规律,用通俗语言也是可以描述的。不同之处在于,无标度网络理论把这些规律量化了。设想一下,我们创立了一个网站,计划与新浪争夺博客名家。风险投资商提供了一笔经费,我们如何合理使用经费,使之发挥最大效能?首先,我们应当出价多少去争取徐静蕾韩寒?第二,是把所有资金集中起来争取几个顶尖的博客高手,还是分散资金吸引为数更多的二线博客写手,这两个策略哪个更有效能?优化类似的投资决策,我们需要量化的数学模型作为决策辅助工具。虽然无标度网络理论目前还没有非常成熟,离胜任这样的决策辅助工具还有很长的路要走,但是至少,它开辟了一个道路,为进一步的研究提供了宝贵的开创性思路。
真是牛人啊
但是貌似第一句可以修改下
谢谢:作者意外获得【西西河通宝】一枚
鲜花已经成功送出。
此次送花为【有效送花赞扬,涨乐善、声望】
[返回] [关闭]
多谢施主。惊喜地发现,已经有四枚通宝了。
每个新人都有一个,你送了一个,还有两枚不知道什么时候得的。
金字塔型是一种比较稳定的社会结构。所谓现代“橄榄型”其实也是一个个更小的金字塔型组成的。
不过互联网确实有可能催生出新的形态,互联网可以看作是一场社会的革命。
如何神经单元只要两个简单信息处理程序就可以建筑这个模型。
1。 相信来自过去提供有效信息的来源的信息。
2。 如果来自多个信息来源的信息越一至,信息越有效,越值得传播。
中枢是信息正反馈的吸引子,因为神经单元都想经过尽量少的信息连通管道,和信息连通次数来获得有效信息。
电磁波不是被发明出来的吧?笔误?
从上下文看,“随机分布”应当是正态分布之误。其实单个人结识人数的分布不可能是正态分布,因为这个人数不会小于0。
到底这个人数服从什么分布?只要考察一个人在单位时间内能够结识的人数就行了。这跟排队论中的顾客到达人数是同一类问题。这个问题的结论就是:服从指数分布,也就是下文说的幂次分布。
期待下文