- 近期网站停站换新具体说明
- 按以上说明时间,延期一周至网站时间26-27左右。具体实施前两天会在此提前通知具体实施时间
主题:【原创】闲扯雷达(一)——从中国余数定理开始 -- 代码ABC
有一堆桃子,两个人分多一个,三个人分少一个,五个人分多两个,请问一共有多少个。很久以前碰到过这个题目,不过当时不知道这是大名鼎鼎的中国余数定理的一个例题,只是当作大人作弄我们这些个小聪明的一种手段。知道这个定理的时候是很久之后的事情了……
再次相遇是在雷达技术的课本中。
跳跃性有点大,事情是这样的。我们知道雷达是靠接收反射的回波来发现目标的,不过光发现目标还不够,雷达通过回波要分析出目标的其它信息,最常用目标信息的就是距离和方位。方位先做个坑留下,我们看雷达是怎么测距的。
测距大家可能觉得很简单,不过就是发一个信号出去,然后等待回波,然后记录发出信号和收到回波的时间差,然后计算无线电波在这段时间里传输的距离再除以二(折返)不就可以了吗。理论上是这样,但实际操作起来就有些不同。实际雷达的测距是持续进行的,对于脉冲多普勒雷达来说,发出去的信号是一系列连续的脉冲,接收的回波也是一系列的脉冲。如果每秒发送的脉冲数量——脉冲重复频率——多到一定程度之后。回波脉冲有可能会在若干个周期后才收到,在无法确定回波脉冲是由哪个发送脉冲得到的情况下,也就无法测定目标距离了,这种情况术语称为距离模糊。图1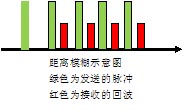
有人会说,如果记下在接收回波前共发送了多少个脉冲不就解决问题了吗?这个方法在示意图中看上去好像是可行的,但是在实际中无法做到。因为你无法知道发现目标时到底是哪个脉冲起作用。示意图中暗示了是第一个脉冲发现了目标,然而也可能是第二个。比如隐身飞机接近到一定距离后打开弹舱向你发射导弹。另外由于干扰或其它的一些原因我们很可能会丢失若干回波。所以在发送的脉冲没有标记的时候,高脉冲重复频率肯定会带来距离模糊。典型的脉冲多普勒体制的雷达,工作在高脉冲重复频率是,其重复频率都在100k Hz以上,也就是每个脉冲的间隔小于3公里。只要目标距离超过1.5公里,就会出现距离模糊。
还有人会说,那我把脉冲重复频率降下来不就解决了?的确是这样,如果脉冲重复频率小于1.5K Hz,那么距离小于100公里的目标就不存在(测)距离模糊的问题。不过脉冲重复频率的选择对于现在常用的脉冲多普勒体制雷达(PD雷达)是一个很重要的参数。高的脉冲重复频率有其不可多得的好处。
图二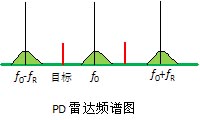
其中一个方法就是利用中国余数定理(终于绕回来了)。其方法如下,采用多个(通常是两个或三个)不同的脉冲重复频率分别对目标进行测距,虽然在这些脉冲重复频率下都存在距离模糊,但问题变成了文章开头的余数问题。实际目标距离是脉冲空间间隔的整倍数与回波在脉间延迟的空间间隔之和的一半。这个倍数我们不清楚,但是在多个不同脉冲空间间隔的帮助下我们可以解出这个不定方程。19世纪高斯给出了这个方程的解法,然而在南北朝的时候中国的《数书九章》就给出了一般算法,所以这个算法也称为中国余数定理。
PD雷达距离解模糊的方法还有好几种,其中一种是连续改变脉冲重复频率使得目标回波落在脉冲间隔中间,通过对频率求导可以得到正确的距离,但是精度比较低。另一种方式就是用某种方式为发出去的脉冲加上标记,这样就可以知道回波到底是哪个脉冲的结果。常用的方式有线性载波调频和正弦波载波调频。不过前者测量精度依赖于调频线性度和变化率,后者则反应较慢。
线性载波调频由于响应较快适合于边搜索边测距模式,正弦波载波调频则适合于连续测距模式。两者精度都只有千米级,而不像上述方法可以得到10米量级的精度。同时如果有多目标的话线性调频方式还是会出现模糊或距离幻影。
土鳖扛一会。
图片看不到的话,请打开以下连接外链出处
本帖一共被 1 帖 引用 (帖内工具实现)
余数定理是怎么回事呢,昨天都没敢应。可是这个文章怕是匆匆而就吧。没以前那几个系列耐读,嘿嘿,读的时候思想总卡。
有些小标题可以上色的。会显得更条理一些
感觉余数测距的思路和伪码测距的思路很像。。。
余数测距是同一个发射接收端发射不同的脉冲频率,伪码测距是多个发射端发射,然后根据发射端之间的相对位置进行解析定位。
当时有点睏,而且在网上找不到想要的图,要自己手工画,郁闷。
三人同行七十稀,五树梅花甘一枝,七子团圆整半月,除百零五便得知
什么时候你给科普一下?你那个数学系列很有意思啊。
多谢!
怎么是我得宝,应该是楼主的吗
鲜花已经成功送出。
此次送花为【有效送花赞扬,涨乐善、声望】
首先花好文。勾起了我痛苦的回忆。。。不过觉得lz介绍还是不太科普,有几个地方不太清楚:
为什么呢?从理论上看不出为什么距离模糊这个问题会消失了啊。不管你电路的gating做的怎么好,你总是有可能接收到更远处的回波吗。
是不是因为实际中超过100公理雷达波已经发散或者衰减到noise floor以下,所以就不用考虑了?但是这样的话,是不是100公里就是雷达的最大探测距离?我记忆中雷达距离比这个大很多啊。
lz这里提到的精度应该指的是成像解析度(resolution)的意思吧?那对于pulse-echo模式来说,解析度应该由pulse长度决定。pulse理论上的最短值,也就是最大解析度应该由雷达发射频率决定。其他方法不过是对这个pulse进行编码,编码过程中使pulse变长从而减低了解析度和增加计算的复杂度(但是我想现在dsp技术那么发达,很多计算的时间已经可以忽略不计了吧)。
我对编码的理解是,通过增加脉冲的能量,可以在不改变工作频率的前提下增加成像距离。但是因为增加了脉冲长度,所以牺牲了成像的解析度。
所以这里
外行一点浅见,还望斧正。
不是说此雷达收不到一百公里以外的回波。
为什么呢?从理论上看不出为什么距离模糊这个问题会消失了啊。不管你电路的gating做的怎么好,你总是有可能接收到更远处的回波吗。
是不是因为实际中超过100公理雷达波已经发散或者衰减到noise floor以下,所以就不用考虑了?但是这样的话,是不是100公里就是雷达的最大探测距离?我记忆中雷达距离比这个大很多啊
100公里 X 1500 X2 是电磁波一秒钟传播的距离。这个问题和信号强度无关。不是测不到而是“模糊”。
说的还是测距,不是成像。要实现大的雷达威力,也就是探测距离,要求大的能量。脉冲能量等于功率乘以时间。如果脉冲时间长会带来测距模糊。
是不是指的雷达一次连续发N个脉冲,这N个脉冲的PRF是1.5K。而下一次再发N个脉冲的时间和这一次之间要隔上一定的时间?
我理解成是以1.5K的频率连续的发射脉冲了。
至于你第二个提示,我还是没看懂。为什么脉冲时间长会带来测距模糊?我觉得只会影响成像精度。