- 近期网站停站换新具体说明
- 按以上说明时间,延期一周至网站时间26-27左右。具体实施前两天会在此提前通知具体实施时间
主题:【讨论】【跟进】趣味数学题 (二) -- 数值分析
这个帖子是 @任爱杰 老兄 趣味数学题 https://www.ccthere.com/article/4616219 的跟进
@任爱杰 老兄原帖转载了我在别的地方发的一个数学题,引发了大家热烈的讨论.
首先我要衷心感谢 @任爱杰 老兄转载. 如果不是他转载我的问题,我就白白错失了很多有趣有益的回复,错失了很好的学习的机会.
其次,我要愤怒声讨老铁的这个限制回复的系统.昨天我已经单发了一个帖子抱怨这件事. https://www.ccthere.com/topic/4616491 河友你来我往发言,就非得是互相纠缠吵架么?就不能是君子和而不同,在一起好好讨论么?我自己提的问题我自己不能参与讨论,魔幻现实主义论坛啊.问题是你当天不让我发言,一时兴致过后,我要说什么我都忘了啊...
再者我要感谢积极参与讨论的各位河友,这里就不一一列举了,以免挂一漏万.其中特别是 @diamond 老兄, 您是专业搞概率的么?以后还要多多请教.
下面书规正文.
昨天的讨论中有人提到条件概率,比如 @胡一刀 老兄的这个回复: 胡一刀:还是觉得你这个办法不对.
下面 diamond 老兄 回复了 diamond:概率不是这么合成的. 但没有详细说为什么, 我这里展开一下.
这是另一个有趣的数学题.
不知道大家见没见过魔术硬币,就是那种变魔术用的,两边都一样的假硬币. 说现在有这么一套三枚魔术硬币,第一枚两面都是字,第二枚两面都是画,第三枚是正常的,一面字一面画.
现在把这三枚硬币掷在地上,并且用手盖起来.现在随机看一枚硬币,看到的是字.问,这枚硬币是正常硬币的概率是多少. 因为看到一面是字,所以不可能是两面都是画的,这枚硬币是正常硬币的概率应该是1/2.
反过来,如果看到的是画,同理,这枚硬币是正常硬币的概率应该是1/2.
如果强行用条件概率,看到这枚硬币是字是画的概率是各1/2,所以这枚硬币是正常硬币的概率也应该是1/2*1/2+1/2*1/2=1/2.
不过我们都知道,掷了三枚硬币,其中只有一枚正常硬币,这枚硬币是正常硬币的概率应该是1/3啊.
所以,不能这么强行用条件概率.
为啥那么多人转不过弯?而且是我认为很聪明的河友,始终认为第二个孩子是独立事件?
原题
有一天我出门正看见新邻居带着一个6,7岁的小男孩回家.我们一打招呼,邻居介绍说,这孩子是他的儿子.
我心里默默推算,嗯,邻居家另一个孩子也是男孩的概率为三分之一(对,这不是笔误,三分之一,不是二分之一)
这里的话术是让你认为邻居只选同一个孩子出行。但如果邻居有两个男孩,可以随意选择任何一个同行呢?那么排列组合就成了
同行 留家
B1 B2
B2 B1
B1 G2
B2 G1
于是另一个孩子是男孩的概率是二分之一。
如果要严格表达,下面的形式是无争议的:
老王共有两个孩子,都是男孩的概率是多少?答案是四分之一。
老王共有两个孩子,其中一个是男孩,都是男孩的概率是多少?答案是三分之一。
原题的问法其实是故意误导读者。计算结果就取决于读者对题目的解读了。
感觉更多像是信仰:到底掷硬币前后,是否观察,对概率有没有影响?这一点,好像很难说服。![]()
![]()
![]()
专业词就不懂了。1/3还是1/2,问题不在数学计算,在于处理问题的思维方法。
1/3说,其实就是我不管,我就三个硬币,正常币概率就1/3,行为观察不影响结果。这是纯数理计算,抛硬币,看硬币,是捣乱。
1/2,其实就是我们日常解决实际问题的方法。字,事实上已经排除两面花,剩下就是两面字和正常币,所以,1/2。抛硬币看硬币,起到排除干扰因素作用。
所以我们看到一个统计数据,如果不知道数据釆样分析方法,被带坑里机会很大。
一个孩子是男是女,当然是独立现象。 题目设定字面就是如此。
然后出题者解题时问题变成了两个孩子大小性别的问题,而且这个问题还在解题时发生变化,原来只是两个孩子男女的概率问题,听到声音后又增加了大小因素。
我这题目是不是太宏大。。。。。。![]()
第一吧,西西河的年龄结构偏大,那个时候的高中课程没有概率论,如果大学又不是这个专业,时间就忘了。
第二呢,人都是勤于直觉、懒于思考学习。随着年龄增长,不思不考不学不习,也不影响自己吃喝拉撒,更无生命之忧。
第三哈,就是个思维方式的问题——尊重原创![]() 。题主既讲了故事,又给出了答案。我首先想的就是,为什么会是这个答案、道理在哪。
。题主既讲了故事,又给出了答案。我首先想的就是,为什么会是这个答案、道理在哪。
不是1/2。比如你看到字,是正常硬币的字面,和两面都是字的正面或反面,3种情况的概率是一样的。所以正常硬币的概率是1/3,两名都是字的概率是2/3。
看到字,排除两面画,剩下两个硬币,两面字和正常币。替换两种选项并不是随机二选一。这种情况下两面字概率是2/3,正常币概率是1/3。两面画的概率是0,这个不用说了。
设:事件 A 表示 “硬币是正常硬币”, 显然事件A的概率P(A)=1/3;
事件 B 表示 “看到的是字” ,则P(B)=1/2
现在所求的是,“看到的是字”的情况下这枚“硬币是正常硬币”的概率,即P(A/B)
根据条件概率的公式定义:

在这里面P(B/A)是什么意思呢,就是“硬币是正常硬币”时“看到字的概率”,显然等于1/2
所以,接着往下算:
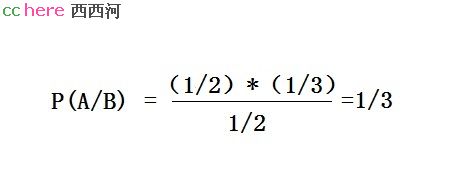
扩展一下:
如果是抛四枚硬币,其中1枚正常,2枚双面字,1枚双面画。随机看一枚,如果是字,则它是正常硬币的概率为1/5;如果是画,它是正常硬币的概率为1/3。
抛五枚、六枚、七枚.........照此办理