- 近期网站停站换新具体说明
- 按以上说明时间,延期一周至网站时间26-27左右。具体实施前两天会在此提前通知具体实施时间
主题:【原创】上帝之书 -- 我爱莫扎特
话说这边儿小毛孩子正和老学霸掐架,四周里里外外倒围了不少群众,可是看戏的多,丢花儿的少。花开二朵,各表一枝,咱们且由他们掐着,回头来看看这非欧几何究竟长什么模样。
其实早在一千多年前,人们就开始研究另一种几何学 ------ 球面几何学。球面上当然没有“直线”,取而代之的是“大圆” ------ 球面上以球心为圆心的的圆。“线段”则是大圆的圆弧。过球上任意不是对径点的两点,都有唯一的大圆把它们连起来。类似的,我们还可以定义两条大圆弧的夹角为相应切线的夹角。遗憾的是,由于任意两个大圆都有两个交点,球面几何并不在欧式几何的体系内(不符合前四个公理)。
球面几何是非常有用的几何,天上(天文),地上(地理)都用得着它。要是没有球面几何学,大航海时代恐怕很难到来,谁让地球是圆的呢?
.jpg)
人们没想到的是,只要稍作一点改动,球面几何就可以转化成另一种不同的非欧几何 ------ 椭圆几何。在这种几何中,过直线外一点的所有直线都与原来的直线相交。历史有时候真会和人开玩笑,我们千辛万苦寻找的东西,其实在很早就摆在我们身边,却不为人所知。这也许就是人们常说的“灯下黑”吧。
我们把球面几何和双曲几何放在一起看,有不少相似的“奇怪”性质。
球面几何里,(三条大圆弧构成的)三角形的内角和总大于180度。我们有

其中S是三角形面积,R是圆球半径,

而在双曲几何里,三角形的内角和总小于180度。我们有

其中S是三角形面积,c是某个正的常数,
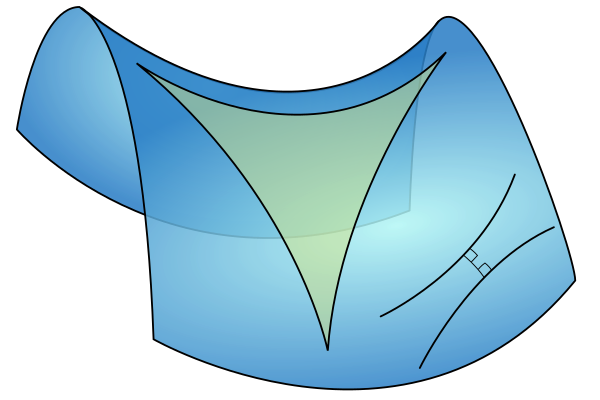
从这些公式可以看出,三角形的面积越小,它越像欧氏几何。今天的我们知道,之所谓我们感觉自己生活在欧氏空间里,是因为我们生活的尺度和宇宙比起来太小太小了。(各位有没有想起狭义相对论?)
再比如说我们已经遗忘很久的勾股定理。前面提到过,勾股定理与第五公设是等价的。也就是说,勾股定理正是欧式几何的“基石”之一。非欧几何里不再成立勾股定理。但直角三角形的三边a,b,c(斜边)还是有些特殊的关系。
球面几何中:Cos(a/R)Cos(b/R) = Cos(c/R)
双曲几何中:Cosh(a)Cosh(b) = Cosh(c)
不过,这还不是勾股定理最后一次出现,后面的篇章中,我们会看到勾股定理更深刻的意义。
类似的古怪公式不少,我就不一一列举了。
科学史上每次出现新生事物总有个被误解然后慢慢被承认的过程。牛顿的无穷小量也好,虚数也好,都在很长的时间里被人们视为“幽灵”。罗巴切夫斯基发现了新的几何后,自己也觉得这个东西实在太古怪。他把这种几何称为“想象的几何”。要人们接受这种想象的几何实在不容易。罗巴切夫斯基试图将双曲几何和人们熟悉的球面几何联系起来,说服人们双曲几何只是球面几何的一个兄弟。他的想法是正确的,但他并未完全成功。
我们的主人公们虽然发现了好东西,可它实在古怪,令人难以相信。伟大的理论还需要优秀的推销员。爱因斯坦碰上了爱丁顿爵士(Sir Arthur Stanley Eddington),让广义相对论少受了几年委屈。若干年后,非欧几何终于迎来了一位好推销员 ------ 意大利数学家贝尔特拉米(Eugene Beltrami)。
本帖一共被 4 帖 引用 (帖内工具实现)
- 相关回复 上下关系8
🙂是这样啊! 我爱莫扎特 字34 2009-02-20 01:11:03
🙂好帖,花一个 4 无梦到徽州 字323 2009-02-18 12:29:31
🙂对,这时候更一般 我爱莫扎特 字87 2009-02-18 12:46:07
🙂【原创】勾股定理(四)--- 古怪的几何

🙂以前一直没意识到这种马鞍面为什么要单独提出来讲 1 熊仔 字62 2009-12-11 20:51:52
🙂好文章,可惜没法送花,只能砌楼了 1 honeybl 字0 2009-02-19 21:24:28
🙂完蛋了,93.75%的读者跑掉了。 2 隔路山贼 字86 2009-02-19 00:01:53
🙂所以我使劲上图来着 2 我爱莫扎特 字140 2009-02-19 00:07:02