- 近期网站停站换新具体说明
- 按以上说明时间,延期一周至网站时间26-27左右。具体实施前两天会在此提前通知具体实施时间
主题:阿波罗尼奥斯问题-Prob. of Apollonius -- 理性网民
共:💬36 🌺127
问题:给定点A和两条直线l、m,找出过A点并与l、m相切的圆(如图)。
解:过l、m的交点做角平分线a。过A点做直线b垂直于a。此时有两种情况:
- 点A不在a上。在b上找到A点关于a的对称点P。所求圆必过A、P两点且与l(或m)相切,可以采用PPL问题的解法。
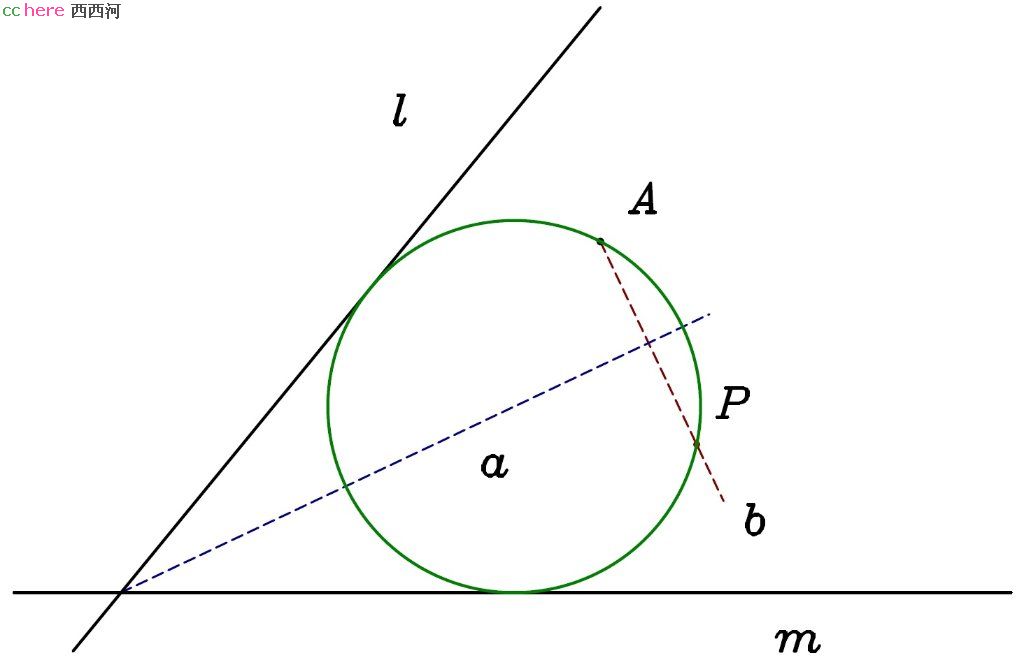
- 点A在a上。延长b与l、m分别相交于P、Q两点。在b同侧及l、m上分别找到R、S两点使得|PA| = |PR|、|QA| = |QS|。所求圆必过A、R、S三点,可以采用PPP问题的解法。
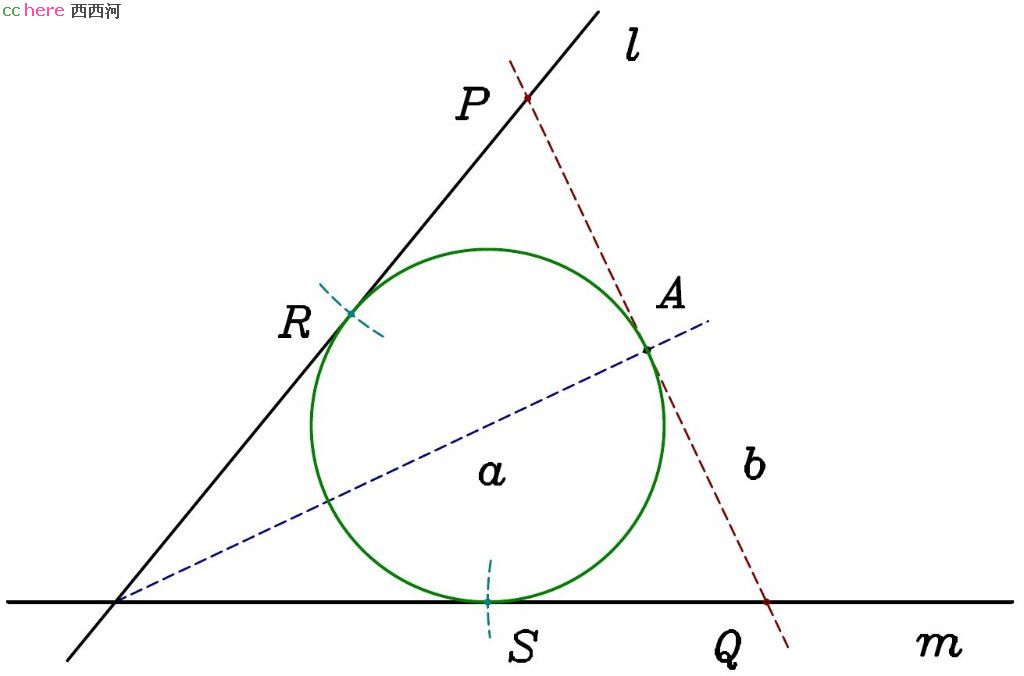
证明:所求圆与l、m相切,故圆心必在角平分线a上,且该圆关于a对称。当点A不在a上时,所求圆同时过A点及A点关于a的对称点P;当点A在a上时,所求圆与b相切于A点。
分析:当l、m相交时,依赖于A点的位置,可以将PLL问题转化为PPL问题和PPP问题求解。当l、m平行时,做与l、m等距的直线a来代替前述解法中的角平分线,可以采用完全相同的解法,将PLL问题转化为PPL问题和PPP问题求解。通常PLL问题有两个解。当l、m平行,且A不位于l、m之间时,PLL问题无解。
关键词(Tags): #几何,
- 相关回复 上下关系8
🙂如果这三个圆是同心圆 2 澹泊敬诚 字174 2020-07-25 09:56:55
🙂解的存在性及个数 3 理性网民 字476 2020-07-27 00:01:09
🙂在PCC之前就搞不定了 理性网民 字177 2020-07-31 15:11:34
🙂【3】PLL问题

🙂【3.2】解的存在性和个数 1 理性网民 字750 2020-10-05 13:55:30
🙂【3.1】解析几何方法 2 理性网民 字2470 2020-10-05 13:54:20
🙂【2】PPL问题 6 理性网民 字1171 2020-07-23 22:03:25
🙂【2.2】解的存在性和个数 理性网民 字555 2020-10-04 17:43:38