- 近期网站停站换新具体说明
- 按以上说明时间,延期一周至网站时间26-27左右。具体实施前两天会在此提前通知具体实施时间
主题:阿波罗尼奥斯问题-Prob. of Apollonius -- 理性网民
阿波罗尼奥斯问题是一个几何问题:“在平面上给定三个圆,如何用尺规作图,找出与这三个圆都相切的圆?”
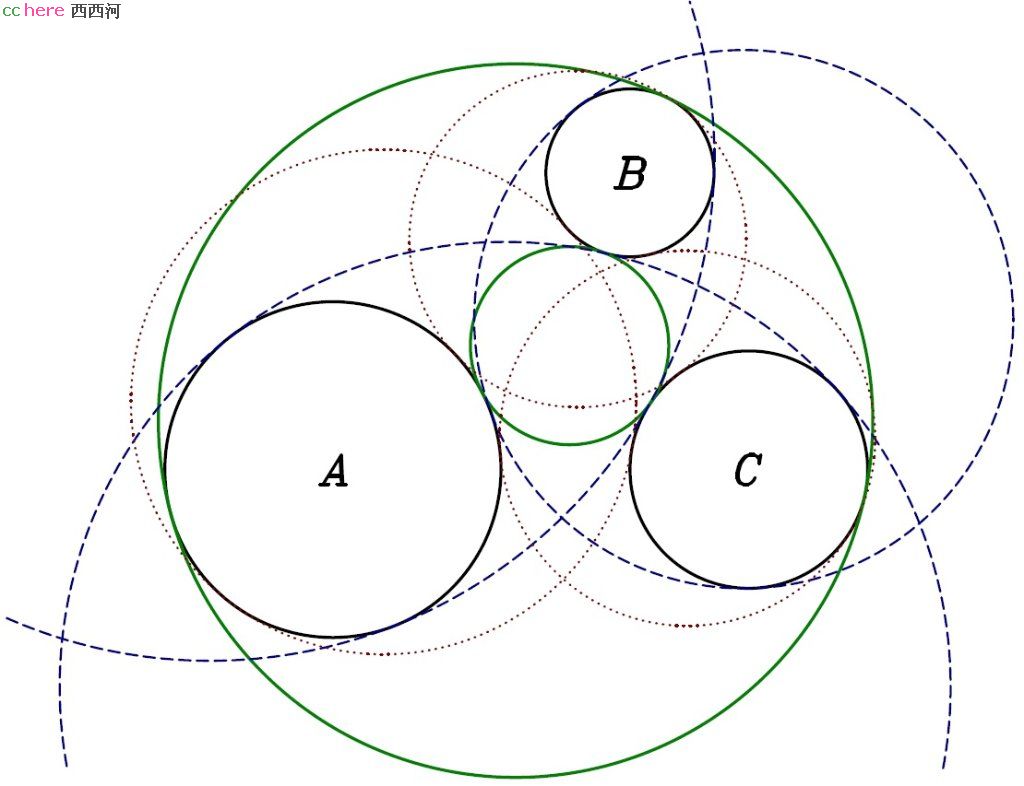
一般而言,阿波罗尼奥斯问题有八个解。这八个解可以分为四组(见图):
- 与三个圆都外切,一个解(绿色实线);
- 与两个圆外切,与剩下一个圆内切,三个解(红色虚线);
- 与一个圆外切,与剩下两个圆内切,三个解(蓝色虚线);
- 与三个圆都内切,一个解(绿色实线)。
阿波罗尼奥斯问题有九种推广形式。在这些推广形式中,给定的圆由给定的点(可以视为半径为零的圆)或者直线(可以视为半径为无穷大的圆)来代替。这样,普遍形式的阿波罗尼奥斯问题可以表述成:“在平面上给定三个几何体,这些几何体是点、直线或者圆的组合,如何用尺规作图,找出经过这些点或与这些直线或圆都相切的圆?”
在这些普遍形式中,给定三个点和给定三条直线的情况都是教科书上参见的尺规作图问题。对于某个普遍形式的阿波罗尼奥斯问题,如果用P表示已知一个点,用L表示已知一条直线,用C表示已知一个圆,那么我们可以用PLC这三个字母的组合来表示某种形式的阿波罗尼奥斯问题。比如说,给定三个点和给定三条直线的情况分别是PPP问题和LLL问题。所有的阿波罗尼奥斯问题罗列如下:
- PPP问题,PPL问题,PLL问题,LLC问题;
- PPC问题,PCC问题,CCC问题
- PLC问题,LCC问题
- LLL问题。
问题:给定三个点A、B和C,找出过A、B、C三点的圆(如图)。
解:连接A和B得到线段l,做线段l的中垂线a。连接A和C得到线段m,做线段m的中垂线b。找到a和b的交点O,以O为圆心、|OA|为半径做圆即为所求。
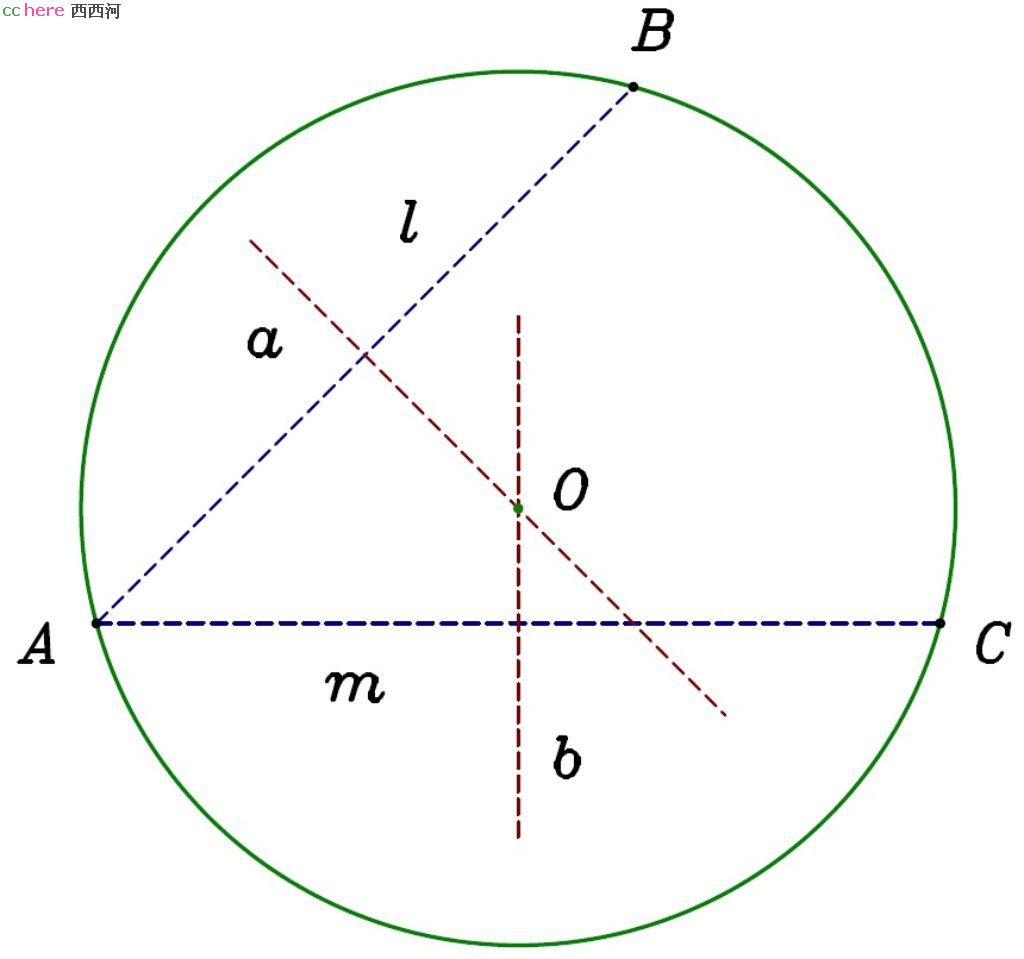
证明:O在线段l的中垂线a上,所以|OA| = |OB|。O同时又在线段m的中垂线b上,所以|OA| = |OC|。那么|OA| = |OB| = |OC|,所以A、B、C三点在以O为圆心、|OA|为半径的圆上。
分析:两条直线a、b最多有一个交点,所以PPP问题最多有一个解。当a、b没有交点时,意味着a、b平行,那么A、B、C三点共线。这种情况下PPP问题无解。
评论:O同时也在以B、C为端点的线段BC的中垂线上。问题所求的圆是以A、B、C为顶点的三角形ABC的外接圆,因而O也是三角形ABC的外心。
问题:给定两点A、B和一条直线l,找出过A、B两点并与l相切的圆。
解:连接A、B两点得到直线m,延长m与l相交于O点。在l上找到点P使得|OP|2 = |OA|×|OB|,那么所求圆必与l相切于P点。这意味着所求圆经过A、B、P三点,可以采用PPP问题的解法。
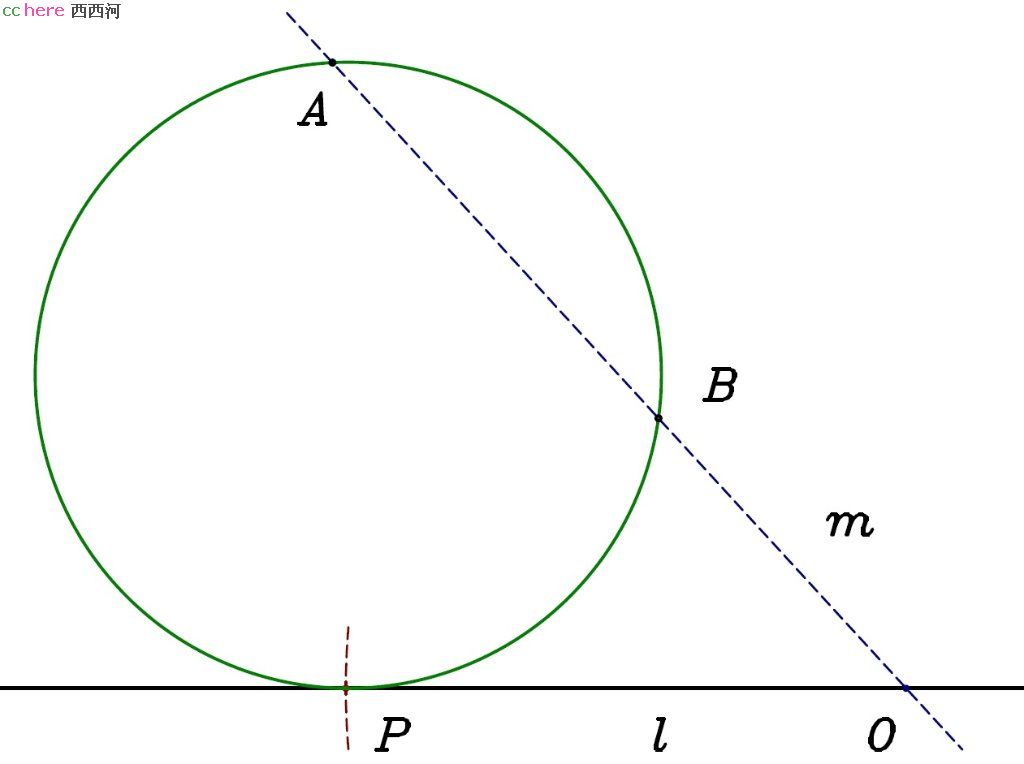
证明:假定l与所求圆相切于P点。那么经过O点直线m与此圆相交于A、B两点,同样经过O点直线l与此圆相切于P点。那么|OP|2 = |OA|×|OB|。这样P点的位置可以由A、B、O三点所确定。
分析:当m与l相交于O点,在l上有两点与O点距离满足等式|OP|2 = |OA|×|OB|。这两点对应于问题的两个解。当m与l平行时,切点P在线段AB的中垂线上。此时问题只有一个解。当A、B两点位于直线l异侧时,PPL问题无解。
评论:PPL问题最终转化为PPP问题进行求解。同时,如果选择O点作为反演变换的中心而且采用合适的变换常数,A、B两点在变换前后变换位置,直线l在变换前后保持不变,而所求圆在变换前后不变。
问题:给定点A和两条直线l、m,找出过A点并与l、m相切的圆(如图)。
解:过l、m的交点做角平分线a。过A点做直线b垂直于a。此时有两种情况:
- 点A不在a上。在b上找到A点关于a的对称点P。所求圆必过A、P两点且与l(或m)相切,可以采用PPL问题的解法。
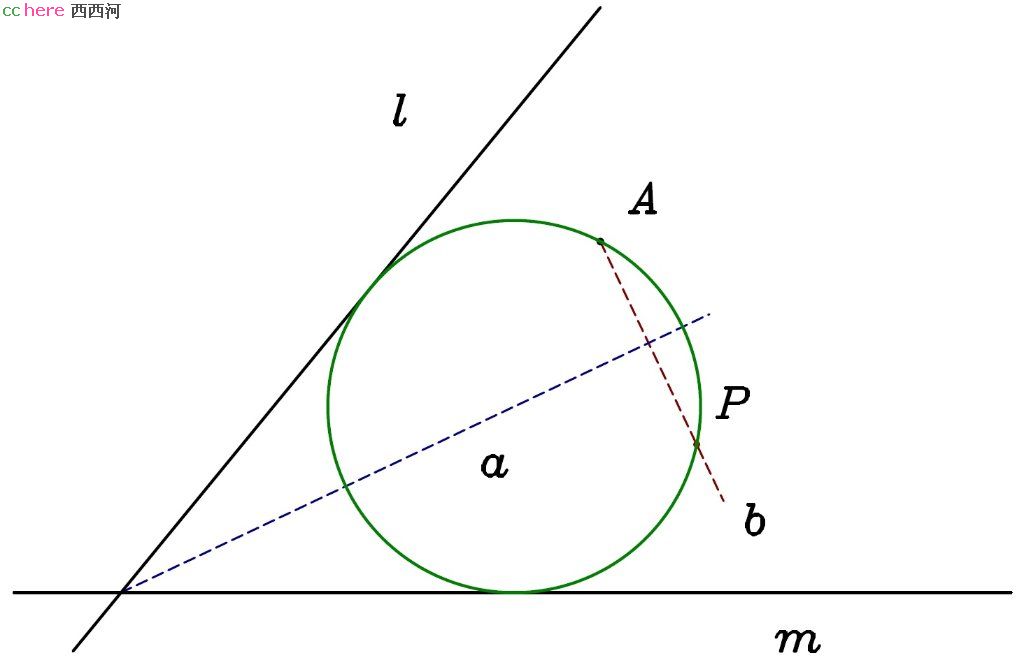
- 点A在a上。延长b与l、m分别相交于P、Q两点。在b同侧及l、m上分别找到R、S两点使得|PA| = |PR|、|QA| = |QS|。所求圆必过A、R、S三点,可以采用PPP问题的解法。
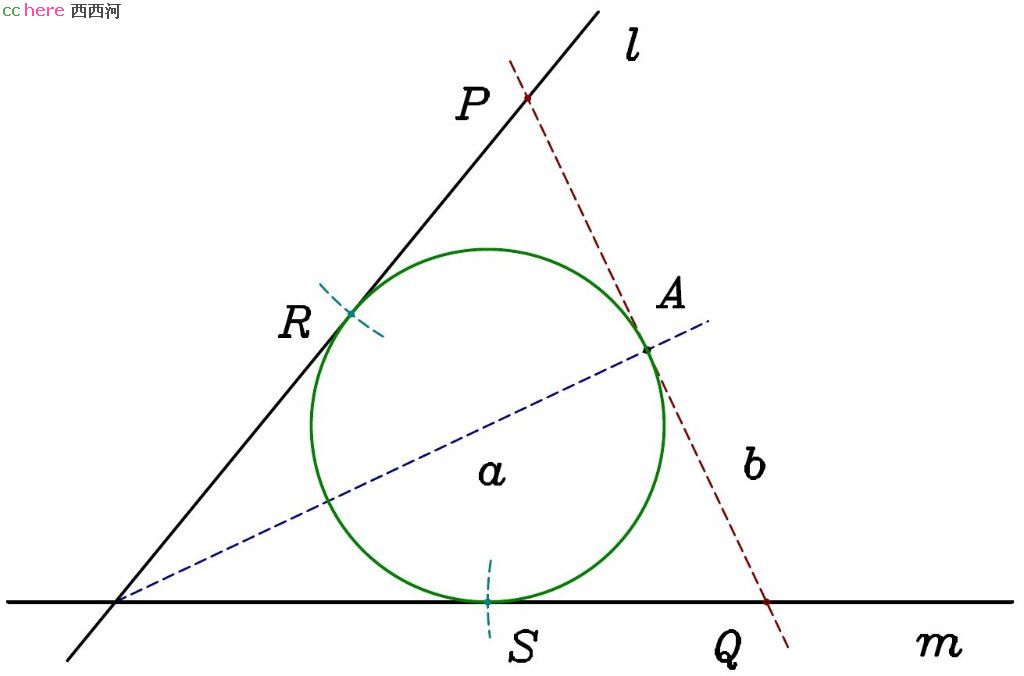
证明:所求圆与l、m相切,故圆心必在角平分线a上,且该圆关于a对称。当点A不在a上时,所求圆同时过A点及A点关于a的对称点P;当点A在a上时,所求圆与b相切于A点。
分析:当l、m相交时,依赖于A点的位置,可以将PLL问题转化为PPL问题和PPP问题求解。当l、m平行时,做与l、m等距的直线a来代替前述解法中的角平分线,可以采用完全相同的解法,将PLL问题转化为PPL问题和PPP问题求解。通常PLL问题有两个解。当l、m平行,且A不位于l、m之间时,PLL问题无解。
问题:给定两条直线l、m和以A为圆心的圆,找出与l、m以及圆A相切的圆(如图)。
解:将直线l、m平移一定距离分别得到直线n、p。该距离与圆A半径相等。过圆心A与直线n、p相切做圆(PLL问题),圆心为O点,与n、p分别相切于B、C两点。过O点做圆与圆A相切,则其同时与l、m相切,故为所求。
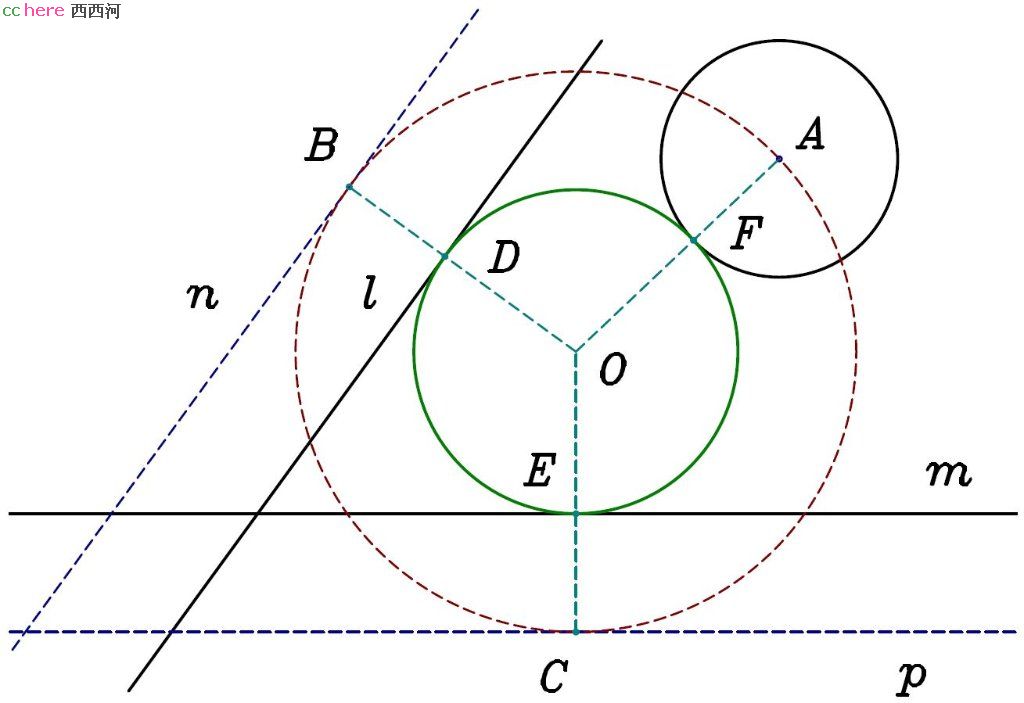
证明:连接O、A两点,那么所求圆与圆A的切点F在线段OA上。同样连接O、B两点及O、C两点,所求圆与l的切点D在线段OB上,所求圆与m的切点E在线段OC上。OB与l、n都垂直,故|DB|等于l、n之间的距离,|DB| = |FA|。同理,OC与m、p都垂直,故|EC| = |FA|。因为A、B、C三点在以O点为圆心的圆上,|OA| = |OB| = |OC|,又|DB| = |EC| = |FA|,所以|OD| = |OE| = |OF|,即D、E、F三点在以O点为圆心的圆上。
分析:在平移l、m时,平移的方向应当同时远离圆A,或者同时靠近圆A。首先考虑l、m相交的情况。当平移的方向为远离时,总会得到两个解,并且得到的圆与圆A外切。当平移的方向为靠近时,依赖于圆A与l、m的相对位置,有两个解或者没有解,并且得到的圆与圆A内切:当圆A与l、m不相交时,或者圆A与l、m都相交时,有两个解;当圆A与l、m中的一条相交时,无解。所以在l、m相交时,LLC问题有四解或两解。类似地可以考虑l、m平行的情况。注意到当圆A位于l、m外侧时,问题无解。
评论:PPP问题、PPL问题、PLL问题和LLC问题组成了阿波罗尼奥斯问题的第一个系列。一般来说,一个系列中排序靠后的问题可以转化为其所在系列中排序靠前的问题。后面可以看到,除了LLL问题以外,所有的阿波罗尼奥斯问题最终都可以转化为PPP问题进行求解(LLL问题也有转化为PPP问题的解法)。
在PPP系列中,我们可以看到两个特别的技巧。其中一个出现在PPL问题中,即反演中心O的存在。这将是后面的PPC问题、PCC问题及PLC问题的求解关键。另一个出现在LLC问题中,即通过直线的平移(及圆的半径的变化),将问题中的某个定圆转化为定点。这将在后面的CCC问题及LCC问题中出现。
问题:给定两点A、B及圆C,找出过A、B两点且与圆C相切的圆(如图)。
解:过A、B两点做圆D与圆C交于P、Q两点。过A、B两点做直线a。过P、Q两点做直线b。两直线a、b相交于O点。在圆C上找到点S满足|OS|^2 = |OA|×|OB|。过A、B、S三点做圆,则其与圆C相切于S点。
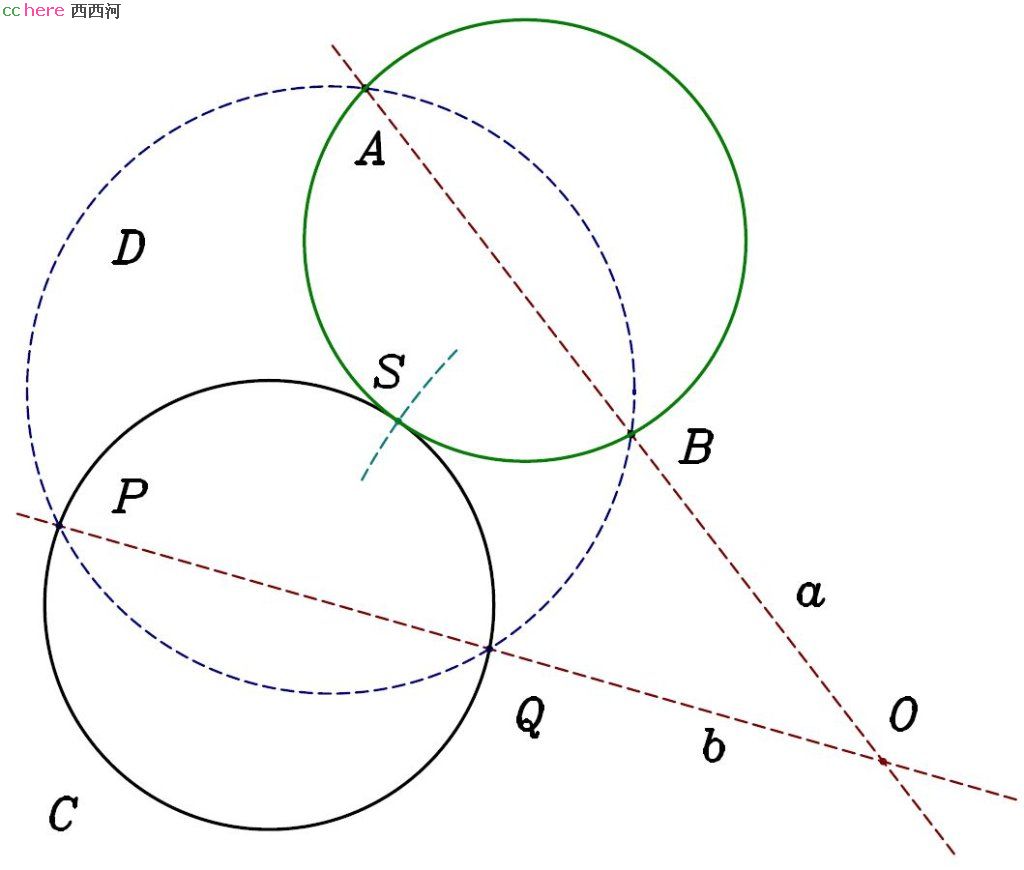
证明:连接OS。因为|OS|2 = |OA|×|OB|,所求圆与OS相切于S点。因为A、B、P、Q四点共圆,|OA|×|OB| = |OP|×|OQ|。那么|OS|2 = |OP|×|OQ|,故圆C同样与OS相切于S点。故所求圆与圆C相切与S点。
分析:当a与b相交于O点,在圆C上有两点与O点距离满足等式|OS|2 = |OA|×|OB|。这两点对应于问题的两个解。当a与b平行时,圆C的圆心与切点S都在线段AB的中垂线上。此时问题同样有两个解。当A、B中有一点位于圆C上时,过此点及圆C圆心做直线。如AB不与圆C相切,则所求圆圆心位于该直线与AB中垂线交点上。此时问题只有一个解。当A、B中有一点位于圆C上时且AB与圆C相切,或者A、B两点位于圆C异侧时,PPL问题无解。当A、B两点位于圆C上,唯一满足条件的圆为圆C本身。解的数目总结如下。
- 两个解:A、B两点同时位于圆C内侧或者外侧;
- 一个解:A、B两点中有一点位于圆C上且AB不与圆C相切;
- 无解:A、B两点中有一点位于圆C上且AB与圆C相切,或者A、B两点位于圆C异侧,或者A、B两点位于圆C上。
评论:点O的位置并不依赖于圆D的选择。从证明可以看出,O的位置实际由圆C及所求圆的公切线所决定。与PPL问题类似,如果采用点O作为反演中心,且选取|OS|2为变换常数,那么在变换前后,A、B两点位置互换,圆C与圆D都保持不变。由于圆D选取的任意性,可以看出,任何过A、B两点的圆都在变换前后保持不变。
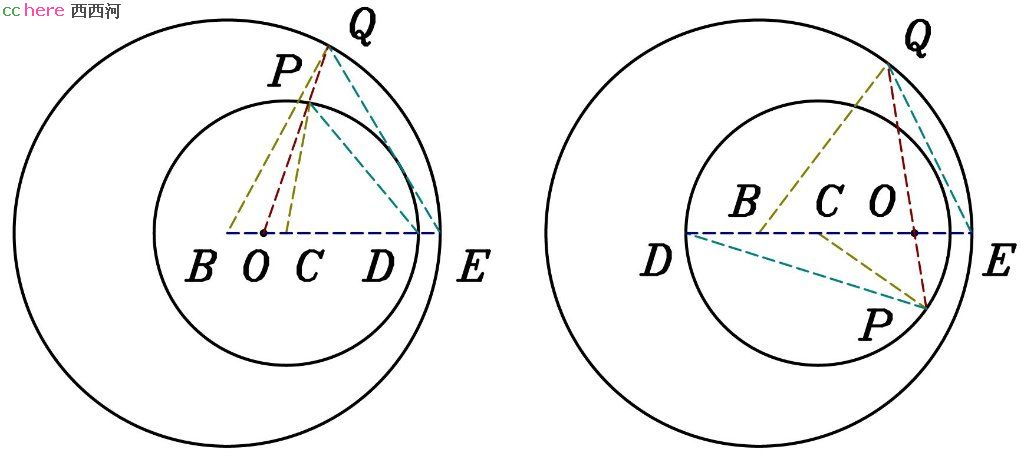
问题:给定点A及两圆B、C,找出过A点且与圆B、C同时相切的圆(如图)。
解:过B、C两圆圆心做直线l,与两圆的公切线m交于O点。两圆与m分别相切于P、Q两点。过A、P、Q三点做圆D,与A、O两点的连线n相交于R点。则所求圆必过R点,可以采用PPC问题的解法。
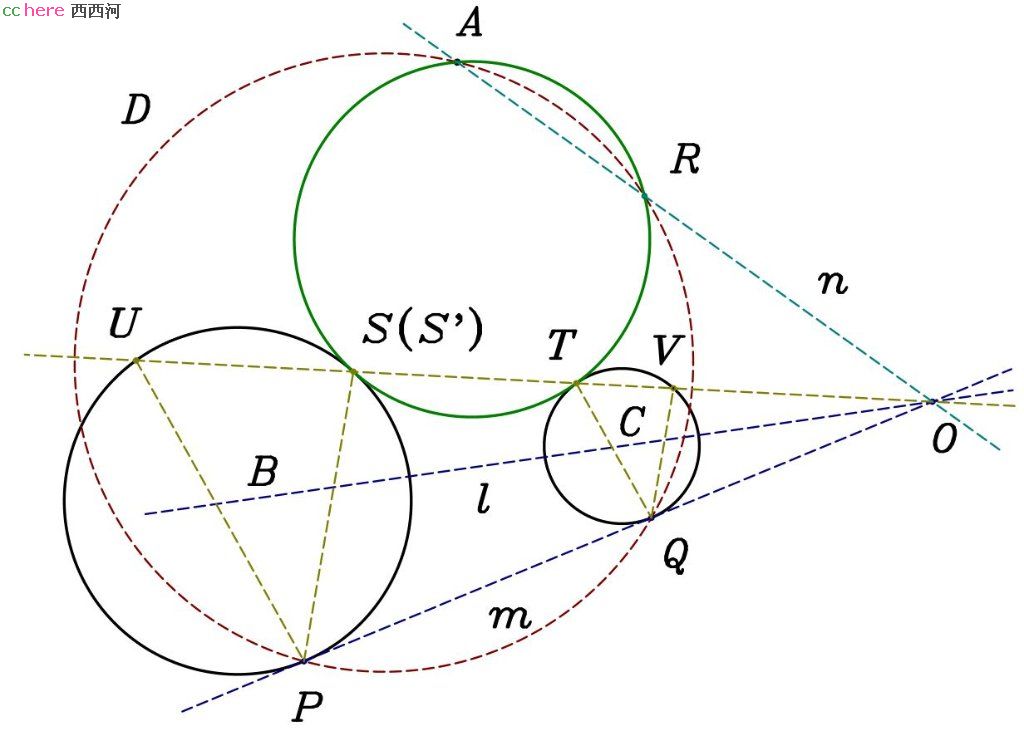
证明:令过A、R两点且与圆C相切的圆与圆C相切于T点。延长OT与圆B相交于S点,与所求圆相交于S′点。现在我们需要证明S与S′为同一点。由于A、R、T、S′四点共圆,|OS′|×|OT| = |OA|×|OR|。又A、R、P、Q四点共圆,|OA|×|OR| = |OP|×|OQ|。故|OS′|×|OT| = |OP|×|OQ|。令OT所在直线与圆B、圆C除S、T两点以外的交点为U、V两点。连接PS、PU及QT、QV。可以证明三角形OPS与三角形OQV相似,三角形OPU与三角形OQT相似,那么|OS|/|OV| = |OP|/|OQ|(等式1)且|OU|/|OT| = |OP|/|OQ|(等式2)。由于m与圆B、圆C分别相切于P、Q两点,|OP|2 = |OS|×|OU|(等式3)且|OQ|2 = |OT|×|OV|(等式4)。由等式1、2可以得到|OS|×|OT| = |OU|×|OV|,而由等式3、4可以得到|OP|2×|OQ|2 = |OS|×|OU|×|OT|×|OV|。综合此二式可以得到|OS|×|OT| = |OP|×|OQ|。与|OS′|×|OT| = |OP|×|OQ|相比较可得|OS′| = |OS|,故S与S′为同一点。这样我们证明了所求圆与圆B有一个交点。假设所求圆与圆B有另一个交点S″,那么连接OS″,可以采用类似的方法证明OS″所在直线经过圆C与所求圆的交点。这与圆C与所求圆相切矛盾。故所求圆与圆B相切与S点。
分析:通常情况下,给定两个圆B、C,可以在BC所在直线上找到两个点满足|OB|/|OC| = RB/RC。得到O点以后,我们可以根据已知点A找到点R并将问题转化为PPC问题求解。由于PPC问题最多有两个解,这意味着PCC问题最多有四个解。
评论:点O在直线BC上,且满足|OB|/|OC| = RB/RC,其中RB和RC分别表示圆B和圆C的半径。如果采用O点作为反演中心,取k2 = (|OB|–RB)×(|OC|+RC) = (|OB|+RB)×(|OC|–RC)为变换常数,那么圆B与圆C在变换前后互换位置,所求圆在变换前后不变。当圆B与圆C外离时,O点可以由两圆的外切线或者内切线与直线BC相交得到。普遍情况下,O点位置可通过将线段BC成比例划分得到。图中以两圆内含的情况为例子,说明以O点为中心的反演变换确实将圆B圆C位置互换。延长BC与两圆分别交于D、E两点,过O点做直线分别与两圆交于P、Q两点。连接BQ、CP、DP、EQ。那么|BQ|即为圆B的半径,|CP|即为圆C的半径。由|OB|/|OC| = RB/RC = |BQ|/|CP|可以得到|OB|/|BQ| = |OC|/|CP|。因为∠BOQ与∠COP互补,所以∠BQO = ∠CPO,也就是说∠OEQ–∠OQE = ∠OPD–∠ODP。因此三角形ODP与三角形OEQ相似。那么|OP|×|OQ| = |OD|×|OE|。这意味着如果我们选取点O为变换中心且|OD|×|OE|为变换常数,圆B与圆C的位置互换。
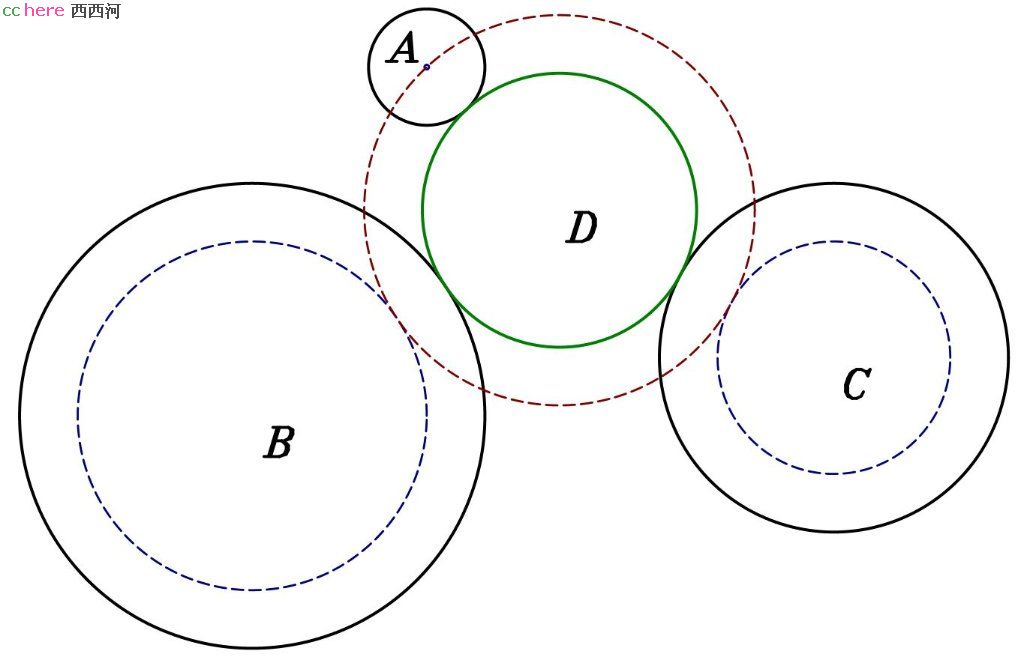
问题:给定三个圆A、B、C,找出与它们同时相切的圆(如图)。
解:不失普遍性,假设圆A半径最小。过B圆圆心做同心圆B′,其半径与圆B差值为圆A半径。同样过C圆圆心做同心圆C′,其半径与圆C差值为圆A半径。过点A做圆D与圆B′、C′相切(PCC问题)。过D圆圆心做同心圆,其半径与圆D差值为圆A半径,即为所求。
证明:由于两圆相切时,切点一定位于两圆圆心连线上。故当圆A、B、C的半径同时增加或减少相同的长度,与它们同时相切的圆的圆心位置不变。这样,我们可以令圆A的半径减小到零,退化为一个点,将CCC问题转化为PCC问题求解。
分析:在上面的求解中,圆B、C可以增大或者减小,故一共有四种组合。每一种组合对应于一个PCC问题。由于每一种组合实际限制了所求圆与给定圆的相切方式(内切或者外切),相对应的PCC问题最多只有两个可行解。这样CCC问题最多有八个解。
评论:PPC、PCC和CCC问题(以及PPP问题)组成了阿波罗尼奥斯问题的第二个系列。在这个系列中,同样可以看到反演中心和圆的缩放是求解的中心技巧。
问题:给定点A、直线l、圆C,找出过点A并与直线l、圆C相切的圆(如图)。
解:过圆C圆心做直线与l垂直,并与圆C相交于O、P两点,与直线l相交于Q点。过A、P、Q三点做圆D,与O、A两点连线相交于R点。那么所求圆必通过R点,可以采用PPL问题的解法(或者PPC问题的解法)。
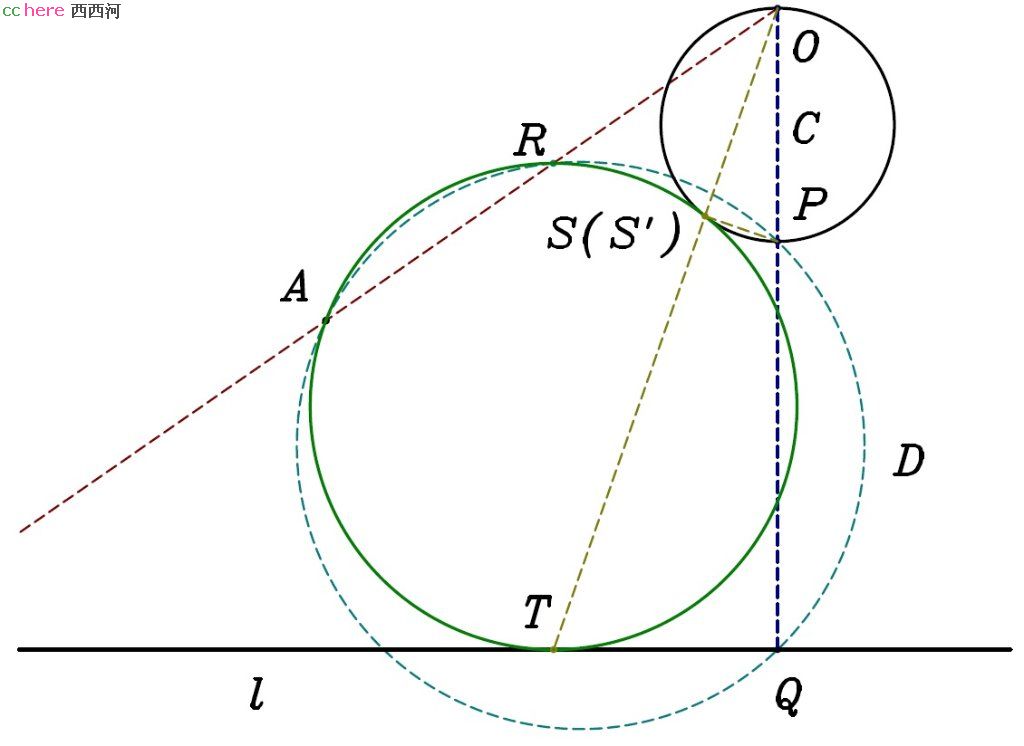
证明:采用PPL解法,假设所作圆与直线l相切于T点。连接O、T两点,与所作圆相交于S点,与圆C相交于S′点。A、R、S、T四点共圆,故|OA|×|OR| = |OS|×|OT|(等式1)。A、R、P、Q四点共圆,故|OA|×|OR| = |OP|×|OQ|(等式2)。连接P、S′两点,则S′在以OP为直径的圆C上,故∠OS′P = 90°。又OQ所在直线与l垂直,故∠OQT = 90°。综合以上可得三角形OPS′与三角形OTQ相似,故|OP|/|OS′| = |OT|/|OQ|,或者说|OP|×|OQ| = |OS′|×|OT|(等式3)。综合等式1、2、3可得|OS|×|OT| = |OS′|×|OT|。故|OS| = |OS′|,也就是说S与S′重合。这样我们证明了所求圆与圆C有一个交点。假设所求圆与圆C有另一个交点S″,那么连接OS″,可以采用类似的方法证明OS″所在直线经过l与所求圆的交点。这与l与所求圆相切矛盾。故所求圆与圆C相切与S点。
分析:在上面的分析中,O点可以位于远离l的一侧,相应的PPL问题最多有两个解。类似的,O点可以位于靠近l的一侧,相应最多可以得到另两个解。这样PLC问题最多有四个解。
评论:如果以O点为反演中心,|OS|×|OT|为变换常数,那么在变换前后圆C与直线l互换,所求圆保持不变。如果我们把直线l看成半径无限大的圆,PLC问题与PCC问题一模一样。
问题:给定圆A、圆B和直线l,找出与圆A、圆B、直线l同时相切的圆(如图)。
解:不失普遍性,假设圆A半径小于圆B半径。过B圆圆心做同心圆B′,其半径与圆B差值为圆A半径。将直线l平移得到直线m,平移的距离等于圆A半径。过点A做圆D与圆B′、直线m相切(PLC问题)。过D圆圆心做同心圆,其半径与圆D差值为圆A半径,即为所求。
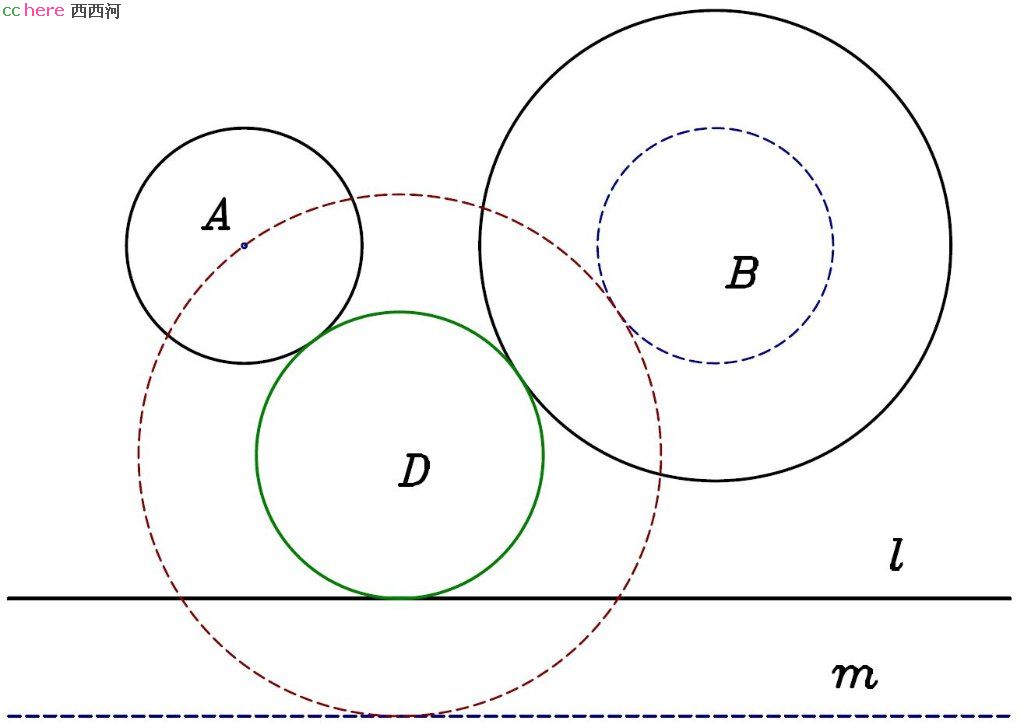
证明:由于两圆相切时,切点一定位于两圆圆心连线上;圆与直线相切时,切点与圆心的连线与直线垂直。故当圆A、圆B的半径同时增加或减少相同的长度,且将直线l平移相同的长度,与它们同时相切的圆的圆心位置不变。这样,我们可以令圆A的半径减小到零,退化为一个点,将LCC问题转化为PLC问题求解。
分析:在上面的求解中,圆B可以增大或者减小,且直线l可以有两个平移的方向,故一共有四种组合。每一种组合对应于一个PLC问题。由于每一种组合实际限制了所求圆与给定圆的相切方式(内切或者外切),相对应的PLC问题最多只有两个可行解。这样LCC问题最多有八个解。
评论:PLC和LCC问题(以及PPP问题、PPL问题或者PPC问题)组成了阿波罗尼奥斯问题的第三个系列。在这个系列中,同样可以看到反演中心和圆的缩放是求解的中心技巧。特别需要指出,PLC问题与PCC问题之间,LCC问题与CCC问题之间,无论是解法还是证明,都有着严格的对应关系。这是因为我们可以把PLC问题和LCC问题中出现的直线看成半径无限大的圆。
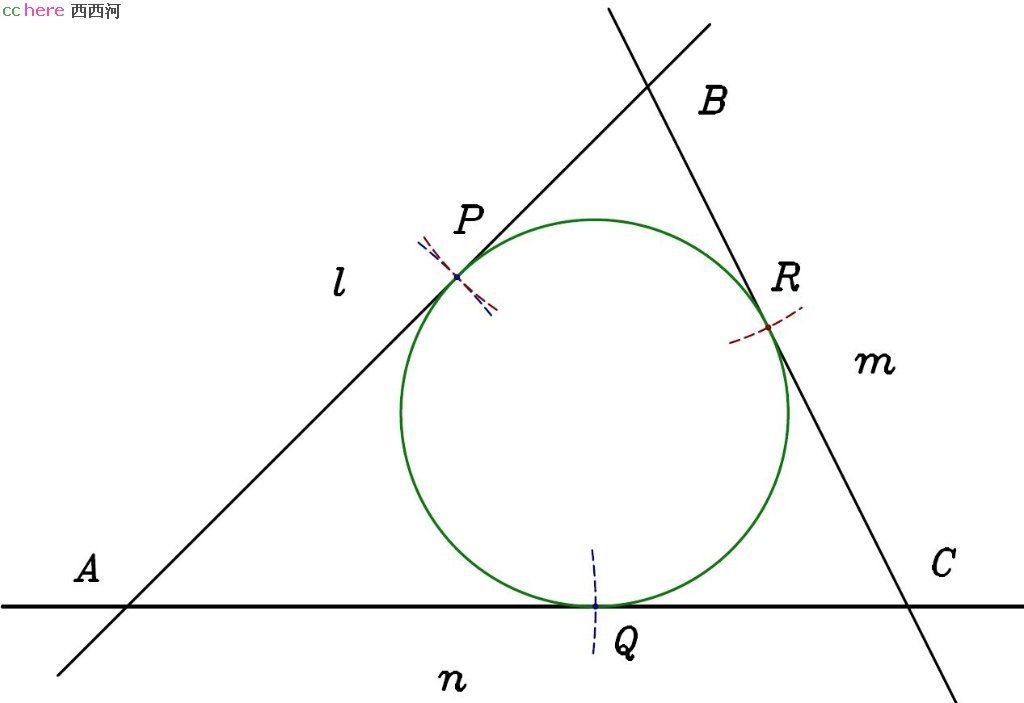
问题:给定直线l、m、n,找出与l、m、n同时相切的圆(如图)。
解:过直线l、n交点A做角平分线a。过直线l、m交点B做角平分线b。直线a、b相交于O点。过O点做直线c垂直于n,且垂足为P点。以O点为圆心,|OP|为半径做圆,即为所求。
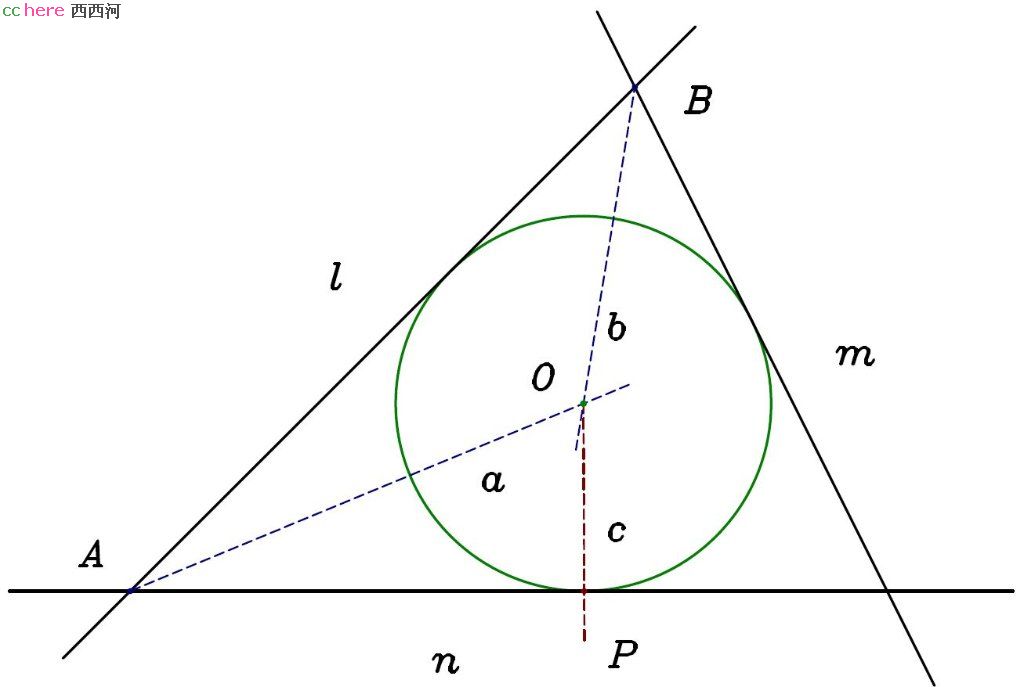
证明:角平分线上的点到两直线的距离相等,故O点到l的距离等于O点到n的距离,且O点到m的距离等于O点到l的距离,且都为|OP|。故以O点为圆心、|OP|为半径的圆与l、m、n同时相切。
分析:在上面的求解中,当三条直线两两相交时,过A点和B点可以分别做两条角平分线,它们的交点都可以做所求圆的圆心,此时LLL问题有四个解。当三条直线中两条直线平行时,LLL问题有两个解。当三条直线相交于同一点时,或者三条直线互相平行时,LLL问题没有解。
评论:LLL问题是阿波罗尼奥斯问题中特殊的一个。通常的解法并不需要将其转化为PPP问题求解。不过下面可以提供另一种思路,将其转化成PPP问题求解。令l与n交点为A、l与m交点为B、m与n交点为C。以A点为圆心、(|AB|+|AC|−|BC|)/2为半径做圆与l、n分别相交于P、Q两点。类似地,以B点为圆心、(|AB|+|BC|−|AC|)/2为半径做圆与m交于R点。过P、Q、R三点做圆(PPP问题),即为所求。可以证明,P、Q、R三点即为所求圆与l、m、n的切点,且|AP| = |AQ|,|BP| = |BR|,|CQ| = |CR|。
应该就无解了吧。进一步地,如果三个圆中有两个存在包含关系,还一定有解吗?或者这个命题要求三个圆不能存在包含甚至重叠?
我尽量会在每个问题的分析中讨论解的存在性及个数,但是我感觉完全的讨论可能很难。我记得我高中时枚举过,所有的情况至少两三百。对于CCC问题,两个圆之间的位置关系有内含、内切、相交、外切、相离(还不算共圆心、圆心位于另一个圆上的情况),三个圆之间的相互关系感觉大概有5×5×5=125种。这么多情况,完全的讨论应该做不到,只能说尽力吧。
PCC问题分析起来感觉一段话绝对搞不定。而且PPC和LLC里面写的感觉也很多错。我准备以后每个问题都补充发个《存在性及解的个数》。
中垂线用尺来画恐怕有些难度。我觉得可以只用圆规,然后用直尺连线。具体做法如下:
1、圆规跨度大于 1/2 AB,以 A 为中心面对 B 画弧,然后以同样的跨距以 B 为中心面对 A 画弧。两弧相交,有两个交点,直尺连接这两个交点,就形成了 AB 的中垂线。
2、同样的做法,选择 A,C, 或者 B,C划弧,连接交点,形成它们的中垂线。
3、中垂线1 和中垂线2 相交,就是圆心。
|OP|^2 =|OA| * |OB| 这个关系是怎么得来的?是不是有很简洁的证明?
另外在 A、B 分别在 l 线的两侧时,上面的算术关系依旧可以成立,但是确实没法画出个圆来,这个又是怎么证明来确定无解?
你的解法是全的。我省了一些步骤,让证明尽量简短。在这个例子中,主要是中垂线辅助的两个点除了做中垂线以外没有什么用处,我就没画了。
之后我也会省掉很多中间步骤,看来有必要把这些中间步骤都补上。我琢磨琢磨是应该放最后弄个附录还是附在它们出现的第一个问题的下面。
如图,已知圆O及圆外一点P。过P点做直线与圆O相交于A、B两点。过P点做直线与圆O相切与C点。我们将证明三角形PAC与三角形PCB相似。因为这两个三角形共有一个顶点P,所以我们只需证明∠PAC = ∠PCB。
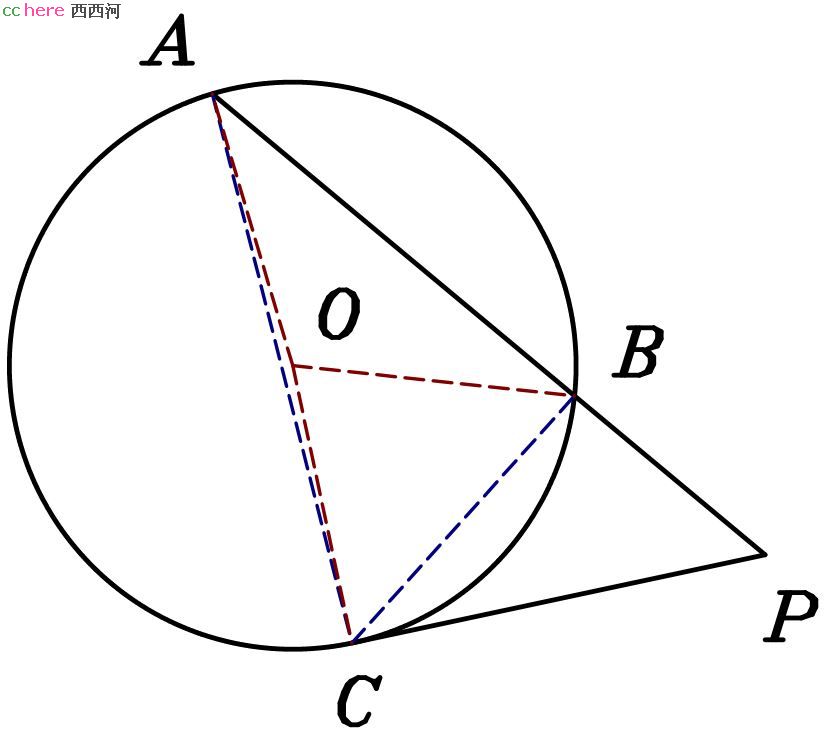
连接OA、OB、OC。PC与圆O相切于C点,故OC与PC垂直,∠PCB+∠OCB = 90°(等式1)。又B、C两点在圆O上,三角形OBC为等腰三角形,故∠BOC+∠OCB+∠OBC = 180°(等式2)且∠OCB = ∠OBC(等式3)。综合式2、3可得∠BOC+2∠OCB = 180°(等式4)。综合式1、4可得∠BOC = 2∠PCB。
同理,三角形OAB及三角形OAC都是等腰三角形,故∠OAC = ∠OCA且∠OAB = ∠OBA。利用三角形ABC的内角和为180°,180° = ∠BAC+∠ABC+∠ACB = ∠BAC+∠OBA+∠OBC+∠OCA+∠OCB = ∠BAC+∠OAB+∠OCB+∠OAC+∠OCB = ∠BAC+(∠OAB+∠OAC)+2∠OCB = 2∠BAC+2∠OCB。这等价于∠BAC+∠OCB = 90°(等式5)。注意到图中O点在三角形ABC的内部,但式5的成立并不需要O点在三角形ABC的内部。综合式4、5可得∠BOC = 2∠BAC。
这样我们得到∠BOC = 2∠PCB且∠BOC = 2∠BAC,故∠PCB = ∠BAC。故三角形PAC与三角形PCB相似。故|PA|/|PC| = |PC|/|PB|,故|PC|2 = |PA|×|PC|。
第二个问题我觉得可以这么理解,要是有个圆与所给直线相切,那么这个圆必然在这个直线的某一侧,它不可能过位于直线异侧的两个点。