主题:趣味数学:从自然数总和为-1/12,到素数定理到黎曼猜想 -- 思想的行者
复变函数有一个魔法,它会告诉你
1+2+3+4+……=-1/12
1+4+9+16+……=0
1+16+81+256+……=0
第二个式子是1平方加2平方加3平方加4平方一直加下去
第三个式子是1四次方加2四次方加3四次方加4四次方一直加下去
第一个式子相信只要上过中学的第一眼看上去就觉得肯定不对,怎么可能正数加正数加着加着变成负数了
第二个式子和第三个式子也让人觉得不可能,怎么可能正数加着正数变成0了
但实际上复变函数论断言
所有的偶数次方,从1加到无穷大都等于0
这是为什么呢?
人们说互联网上啥都有,只要有问题就会有答案。
但很遗憾的是我搜索中文互联网,就没有几个答到了点子上,大都是牵强附会的回答。
实际上,要理解以上式子,就要理解复变函数的一个魔法叫做复函数的解析延拓。
在复函数中,一个函数的解析范围可以比另一个函数的解析范围大,而且在双方都解析的情况下,两者又都相等,那么这个时候,解析范围大的函数称为解析范围小的函数的解析延拓。
什么叫做函数的解析?
当一个函数加着加着变成无穷大了,这个函数就是不解析的,这个变成无穷大的函数是没有意义的或者说是发散的
回到前面的式子
1的-s次方+2的-s次方+3的-s次方+……
这个函数我们在前面介绍过了,是欧拉这个数学英雄发现它具有将连加变成连乘性质的名叫zeta(泽塔)函数即ζ函数
这个ζ函数在一般情况下只有s大于1才不会加着加着加到比任何一个数都大
即在一般情况下只有s大于1,这个函数才有意义。
但如果只能研究s大于1的情况,就没有黎曼后面的伟大的发现了。
黎曼发现,将上面的ζ函数变成一个积分,可以把这个函数变成一个在s更小很多的时候依然不会变成无穷大的函数,而且在s大于1的时候,两个函数又完全相等。
函数解析范围扩大,术语就叫做函数的解析延拓。
黎曼把ζ函数解析延拓成了什么样子呢
本人记性不好,记不住,只好拍照了
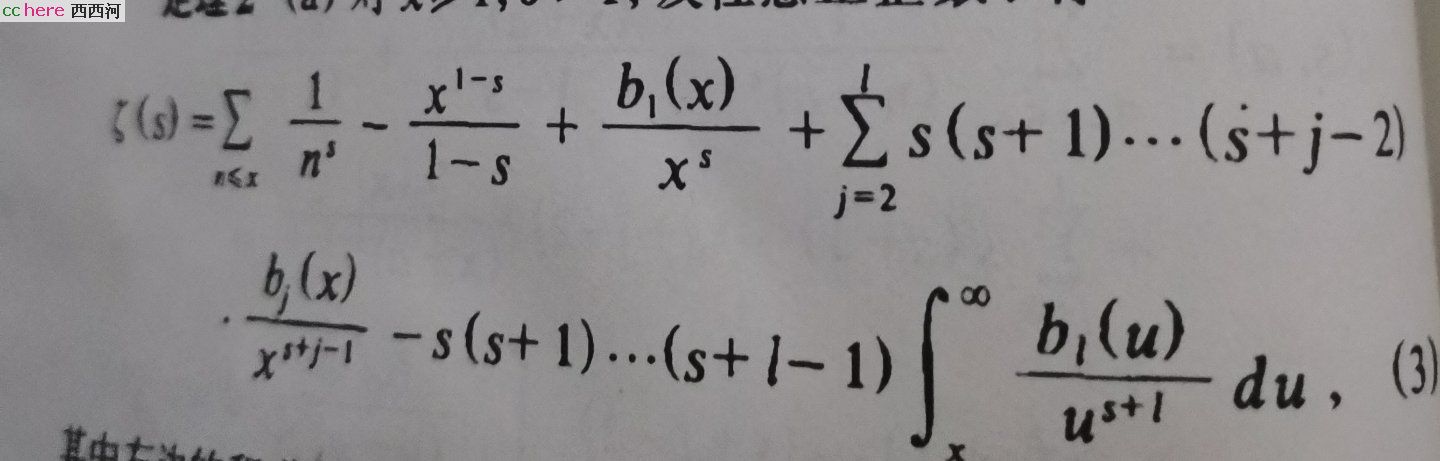
为啥1加2加3一直加下去变成负数了?
因为这里的1+2本来就不等于3这里的1+2其实就等于
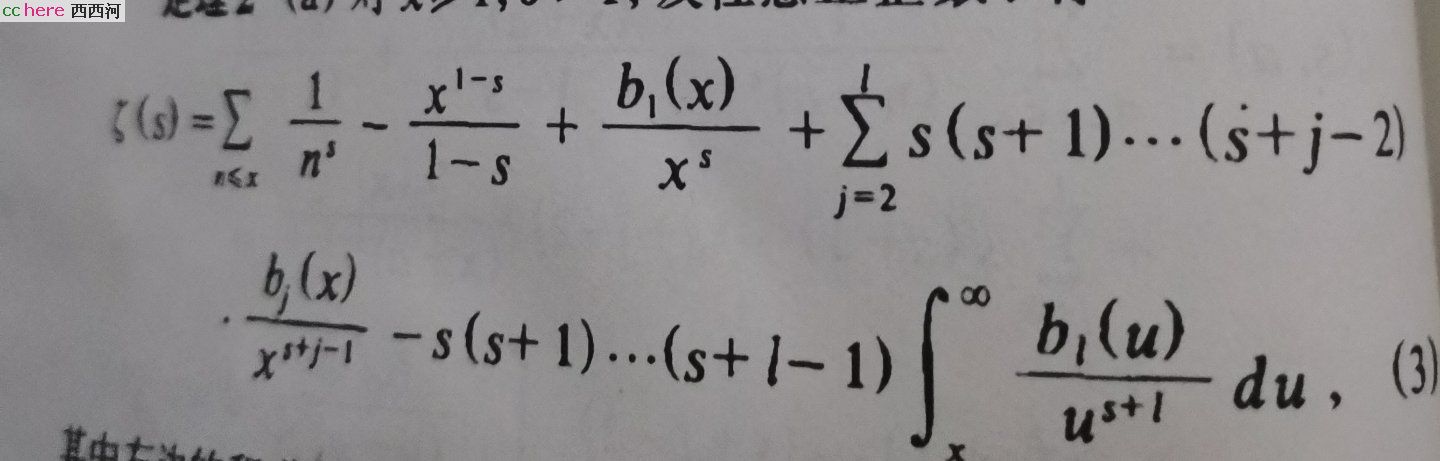
上面的式子中取x=2就是1+2的值,显然这个值不等于3
那么为什么要解析延拓呢?
因为我们需要把这个函数比较重要的点给圈起来,然后对这个圈圈做积分。
这个ζ函数有一个最重要的点是s=1这个点。
这个点是不管你怎么做魔术,ζ(1)都会比任何一个数都更大,即s=1是ζ(s)的极点,做积分的时候需要把这个极点给包进去。
把这个极点包进去了,就可以很显然的得到高斯——这个数学王子在此前就素数研究而得到的一个结论。
高斯曾经就素数个数给出过一个相当精确的估计,并且完败了勒让德。
高斯是怎么估计素数个数的,黎曼怎么证明高斯的估计的,且听下回分解。
- 相关回复 上下关系5
🙂趣味数学:从自然数总和为-1/12,到素数定理到黎曼猜想 9 思想的行者 字4687 2024-09-05 12:02:47
🙂复变函数的变身法:为啥1+2+3+…=-1/12

🙂(三)数学王子的接班人:爱画圈圈的黎曼 2 思想的行者 字4232 2024-09-12 10:46:32
🙂几百年风风雨雨,虚数走上历史舞台 5 思想的行者 字7358 2024-09-08 00:51:39
🙂附录:复变函数的奇妙性质,为什么从1加到无穷大等于-1/12 1 思想的行者 字587 2024-09-12 11:04:13