主题:趣味数学:从自然数总和为-1/12,到素数定理到黎曼猜想 -- 思想的行者
本人一直对数学很感兴趣 但是长期以来,我很难准确记住一个公式,随着我把中学的不愉快的或者过度亢奋的记忆慢慢清除,我的记忆力开始有了较大的恢复,现在也就可以写一些科普性质的小文章,主要目的是为了揭示数学的趣味性和美以及人们在探索过程中发生的一些事情
(一)
素数是无限多的,古希腊人最初的发现
一个自然数可以分成素数和非素数,这个在今天的人们看来是很显然的,但是第一个提出自然数可以分为素数和非素数的人不简单。
大概也没有人能够考证出是谁首先提出素数和非素数的分类 唯一可以肯定的是不是中国人,中国古代文献诸如九章算术周髀算经等等没有素数相关的内容。
但数学史上明确记载了一个古希腊人欧几里得,也就是我们初中学的几何的创造者,欧几里得第一个给出了素数有无穷多个的证明
欧几里得的证明很简单,我在初中参加数学兴趣小组的时候就看到了欧几里得的证明
假定所有的素数是p1,p2,p3………
我们设X=p1p2p3……+1
即x是所有的素数的乘积再加1
这个数X不可能被p1,p2,p3等等素数整除,因此要么X是一个新素数,要么X还有新的素数因子
因此素数个数不可能是有限的,素数个数只可能是无限的。
我初中的时候看到欧几里得的证明觉得这个证明很美。
(二)数学英雄欧拉来了
欧拉被人们赞誉为数学英雄,因为他做的数学贡献实在太多了
随便举几个例子,我们中学就学到的把自然对数和三角函数联系在一起的公式
e**(xi)=cosx+sinxi
我还记得当年课堂上数学老师用一种夸张的声调说好美啊,这个公式。
这个公式把指数函数和三角函数联系在一起 实际上成了推开复变函数大门的钥匙,下面我们会讲到复变函数。
但我们今天看到的这个看起来简单的公式是微积分发展到一定阶段以后才能证明的。
牛顿发明了微积分以后,马上就开始研究级数
例如e**x,logx等等怎么样把它变成一串长长的长长的长长的……无限长的函数的相加
例如1/(1+x)=1-x+x**2-x**3+……
log(1+x)=x-1/2x**2+1/3x**3-………
牛顿们发现,很多函数都可以这样,把它变成长长的一大串(当然牛顿们开始并没有给出严格的证明)
欧拉之所以能够发明上述被很多人认为很美的公式,他做的就是把左右两边都展开成长长的一大串,然后发现左右两边展开的样子完全一样,然后他就给出了那个看起来又简单又美的公式。
欧拉的贡献是说不完的,这里说一个比较不被人知道的就是阶乘函数的推广
最早是哥德巴赫问他,能不能够把阶乘函数n!推广一下,对于一个非整数例如0.5的阶乘怎么算呢。
欧拉收到哥德巴赫的信以后,并没有想多久,很快就给出了答案
欧拉给出的答案是所谓的gama函数,这个gama本来应该写成希腊字母,这里编辑希腊字母不容易
欧拉给出的答案是一个积分形式的式子,总之计算那个积分可以得到s*gama(s)=gama(s+1)
这个gama 函数非常重要 反正很多学科里经常可以看到那个长的像T一样的函数,例如概率论,数论,数论尤其是解析数论与这个gama函数简单是扯得难分难解。
说回到素数问题上来,欧拉这个数学英雄的一个重大发现是他发现了一个函数,这个函数的连加可以表示成一个连乘的形式
这个函数叫做zata函数,显然这也是一个希腊字母,这个字母长的像S这个字母似的,就是多转了一下。
zata函数就是一个无穷多项的连加
即n**(-s)的连加,即n从1加到无穷大
欧拉这个数学英雄发现
这个连加的函数等于1/(1-1/p)的连乘,这里p就是指素数,连乘由最小的素数开始乘起,一直乘下去。
这个数学公式也是非常美的,特别的是此后启发了另外一位大数学家黎曼,然后黎曼在欧拉公式的基础上谱写了新篇章
(三)插播,虚数是如何走上历史舞台的
我们中学时期就学过了虚数,但很多人相信都会有一个疑问,虚数有什么用,虚数是不是客观存在,不用虚数行不行等等。
这个问题在欧洲,很早就有人在思考这些问题了,确实把-1理解成i的平方是不是一个数学游戏,是不是仅仅是一个数学游戏呢,当时是有很多人困惑的。
一个支持虚数的重要性是欧洲围绕高次方程解法得出的结果。
夜已深,先写到这里
1)十六世纪意大利的数学比武擂台
十六世纪的欧洲是文艺复兴的欧洲,人们对于数学问题很感兴趣,甚至常常就数学问题展开价值不菲的赌博。
而当时的中国处于明朝时期,明朝人还没有现代科学意义上的方程的概念。
中国传统的方程概念是一套求解行列式的算法,而西方意义上的方程是指含有未知数的等式以及围绕着这个等式的一个越来越博大深远的理论体系。
十六世纪的意大利,围绕着三次方程的解法,人们对赌了好几回,当时的意大利人把一个数学问题的解法象中国的武林秘籍一样藏起来,然后与人在一个大擂台上摆擂台,遍邀天下英雄:我出一道题给你你会做吗?
不得不说,这种科学的风气是很好的,可以说当时的以意大利人为代表的欧洲人是相当的爱科学,当时的中国明朝的数学风气比欧洲差远了。
几次大擂台举办过后,三次方程的解法已经逐渐的从私人珍藏的武林秘籍到为大众所熟知
三次方程的解的形式有点复杂,需要先开平方,然后再开立方。
例如对于y**3-15y-4=0,这个方程,可以得到这个解
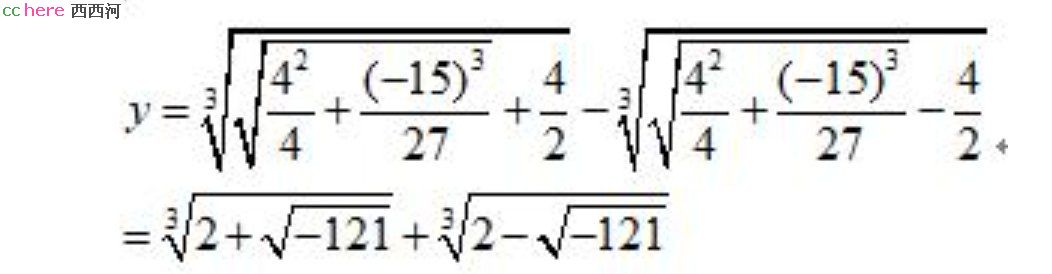
里面包含的-121的开方,如果把它忽略掉就得不到解,而实际上这个方程有三个实数解。
当时的人们可以通过一些比较巧妙的办法把负数的开方绕过去,但是大智若愚,太巧妙的东西往往隐藏了本质的东西,人们开始思考负数的开方也是一类很重要的数。
虚数思想的萌芽正在悄悄的生长
2)十八世纪大英雄欧拉使出了十七世纪费马的剑法
十七世纪的欧洲出了牛顿,莱布尼兹两位大侠,他们创造了全新的剑法,微积分
牛顿使用微积分的剑法三下五除二的解决了开普勒给人留下的难题,即:为什么天体运行以椭圆轨迹运行,(开普勒第一定律)引起整个欧洲的轰动
当年开普勒推出天体运行三大定律的时候在欧洲就是很轰动的,开普勒被欧洲人赞誉为天空的立法者
现在牛顿更进一步的证明了开普勒定律,看牛顿还能够解释天空为什么要那么立法,厉害吧
于是牛顿名闻天下,他的剑法即微积分也因此天下流行。
但实际上牛顿的剑法来自于更早几十年的也是十七世纪生人的费马,这个法国的职业律师。
我看了一些数学书以后,知道费马此人,其开创性基本上可以说前难见古人,后难见来者。
对于费马,中国人普遍不太熟悉,例如
中国人在中学就学习的解析几何,人们知道笛卡尔,却很少有人知道费马
说明一下:当初我在初中自学解析几何的时候对于一条直线能够用一个方程来表达也是感到非常有意思的(当然到了高中,我对解析几何非常烦,因为解析几何题目就一个套路就是解方程,题目做多了了无新意,就很讨厌了)
其实费马也发明了解析几何而且,更进一步的,甚至可以说进了很大很大很大的一步的是费马发现了一点:求曲线的切线的斜率和求曲线的面积是一对反运算。
后来费马和笛卡尔两个人闹了不愉快 ,两人貌似争起了解析几何的发明权,费马说笛卡尔先生:笛卡尔先生请注意:最关键的问题是最大最小的问题,请您注意这一点。
笛卡尔先生则反唇相讥道:是,最大最小先生您说得对。
牛顿为什么能够用数学证明开普勒的天体运行定律,原因就在于牛顿学习到了费马的那个最大最小那一套。
我们今天知道,最大最小就涉及到微分,导数为0的点就是最大值或最小值。
而费马发现的求切线与求面积互逆正是微分与积分的互逆。
费马发明了剑法几十年间无人问津,而独具慧眼的牛顿虽然当时才20出头年纪轻轻,却发现了费马剑法的独特光芒,拿来一用,竟然证明了开普勒定律,而且他还用了开普勒剑法来表述伽利略发现的理论:外力等于质量乘以加速度,提出牛顿力学三大定定律,这也是一个不得了的成就,动力学开始粉墨登场。
与此同时德国的莱布尼兹也同时发现了费马的剑谱,并且开宗立派。
可以说费马的剑谱完全开创了一个新的时代,——微积分的时代
微积分的光芒是非常耀眼的,但是费马先生的发现远远不止这一点,他的发现多了。
例如费马小定理就非常重要
相比于现在为人所熟知的费马大定理,费马小定理虽然简单,但也是非常巧妙,而且对于数论而言,应用非常的广泛
费马小定理是:
n**(p-1)-1能够被p整除(说明一下,本人的记忆力非常差,一起上班n年的同事的名字我都经常记不起来的,以至于同事们经常会考我他叫什么名字,这个定理我是根据记忆写出来的,很可能是错的,不要太相信我的记忆的正确性,你可以查阅书籍或者网上搜索获得正确的公式,包括我在上一篇给的欧拉的连乘连加公式也是记错了,p**(-s)写成p**(-1)
但费马大猜想更出名,因为它很困难。
所谓费马大猜想即x**n+y**n=z**n当n为大于2的整数的时候没有正整数解
二十世纪的英国人怀尔斯证明了费马大猜想,用到了诸如模形式椭圆方程等等现代化的数学理论 但费马说这个猜想他早就证明出来了,不过书的边上位置太小,他懒得写出来。
费马是真的自己证明出了费马大猜想还是他给世界开了一大大玩笑?
考虑到费马这个人那么厉害,他真的用更初等很多的方法证明出了费马大猜想并不是没有可能 这也是后来欧拉他们拼命的去找费马的笔记的原因,但费马确实给出了一个当n=4,方程不存在整数解的证明。
费马的证明用了一个巧妙的办法
无限下降法:
如果方程存在一个解,那么存在一个比这个解的“高”还要小的解……
所谓解的高指的是一个有理数表示为m/n,m和n哪个数更大,那它就是这个有理数的高。
欧拉研究了费马的证明研究了半天——当然这个半天可能是一年甚至好几年,发现如果可以引入虚数,那么就可以证明n=3的情况,这进一步提示了虚数的不可或缺。
以后的剧本是欧拉发现了我前一篇谈到的公式e**(xi)=cosx+i
sinx
需要说明的是当时欧拉并不是用i来表示虚数,这是高斯这个数学王子的创造。
4)数学王子高斯一锤定音
我记得中学时期老师的话:世界四大数学家是阿基米德,牛顿,欧拉,高斯(但今天的我看法有些不一样)。
高斯的数学地位是不一般的,但我对高斯的数学成就不太了解,就数论而言,我只知道他引入了同余式, 以及证明了二次剩余互反律。
另外还有这个高斯和公式:
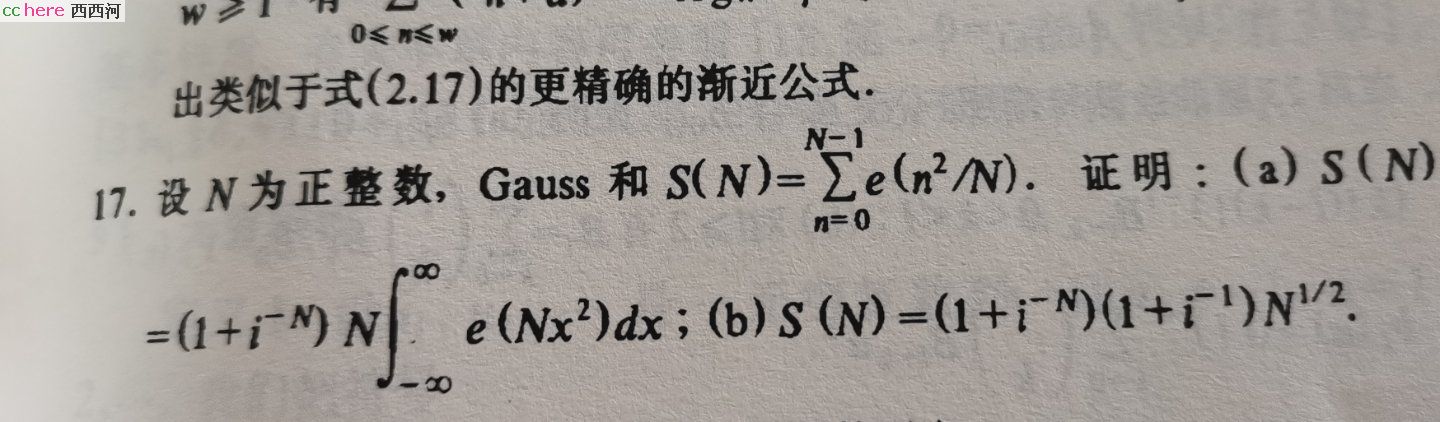
高斯利用这个公式给出了二次互反律的另一个证明
高斯说,以后大家就用i来表示-1的开方吧。
大家异口同声的说:好
于是,在高斯的威望的加持下,虚数i也就正正式式的成为数学大家庭的一个重要成员。
所有的自然数相加等于-1/12,你相信吗?
但这个公式确实是写在书上的。
如果你不相信,还有更奇怪的
1的平方加2的平方加3的平方一直加下去等于0,你信吗?
但确实写在书上,那么多大学者一点都不怀疑。
更进一步的
1的四次方加2的四次方一直加下去又是等于0
1的六次方加2的六次方一直加下去又是等于0
这个式子可以一直罗列下去。
……
很多国人都感到很疑惑,很多人都试图给出解释,包括知乎上想解释以上式子的人真的是各显神通。
前面说到数学王子出马,他证明了一大堆与复数有关的定理以后宣布:以后大伙就用i来表示-1的开方了,然后复数的重要性就没有人怀疑了。
人们开始认真的对待复数,发现复数有很多奇怪的性质,例如一个复数函数常常不仅有一个值,而是有多个数值。
例如对于z的开方,就有两个数值
z的对数函数,则有无穷多个数值
等等。
这一点以后被一位杰出人物利用,他引进了一个观念,使得一个多值的复变函数可以理解为单值的复变函数。
这位杰出人物就是黎曼。
可以说黎曼是数学王子高斯的接班人,为什么这么说?
因为高斯有一天突发奇想,他在研究曲面的时候想,我是不是可以不用坐标系就能够计算曲面呢
曲面用什么来衡量,一个重要直指标是曲率。
曲率就是弯曲的程度
对于一条圆,曲率就是半径的倒数。
也就是说圆的半径越大,那这个圆的曲率就越小,这个圆就越弯的没有那么厉害。
如果不是一个圆呢,而是一条不那么规则的曲线呢?
那就要用微积分来计算了,每一个点上的曲率都不一样。
如果是一个面呢,面上每一个点可以划出无数条曲线,每一条曲线都有一个曲率。
但每一条曲线的曲率都由两条曲线上的曲率来决定,那两条曲线上的曲率叫做主曲率
高斯研究了两个主曲率的乘积的意义,以后人们就把两个主曲率的乘积称为高斯曲率。
爱因斯坦发明了广义相对论,广义相对论就是要计算曲面的高斯曲率。
那一天高斯摆弄了几个数值,发现曲面的面积 曲线的弧长,曲面的曲率等等都可以不依赖于坐标系,只要规定几个指标,计算那几个指标就可以了。
高斯得到那个结果非常欣喜,非常喜悦,让欣快的把他的发现称为绝妙定理。
以后爱因斯坦就是把这个绝妙定理发扬光大,提出广义相对论的。
但高斯年纪终于越来越大了,尽管他是数学王子,但他也有老去的一天,然后他有一天参加一个年轻人的博士资格论文答辩会,眼前一亮。
没错,这个年轻人就是黎曼。
黎曼把高斯的绝妙定理推广到多维空间,然后用了一大堆符号来计算诸如主曲率,高斯曲率等等。
黎曼就是善于推广,下文还会说到他把欧拉的连乘连加定理推广,从而成为了解析数论的奠基人。
黎曼对高斯的定理的推广是很重要的,我们知道后来爱因斯坦研究的就是四维空间,光靠三维空间是不够研究引力的。
还在读博士就推广了高斯绝妙定理,这个年轻人真是出手不凡,称这个年轻人即黎曼为高斯这个数学王子的接班人是一点不为过的。
黎曼不仅推广了高斯绝妙定理在复变函数领域,他也得到了一个非常基本的定理。
更准确的说他是与另外一位法国数学家柯西一起提出了一个柯西黎曼方程
然后有了这个柯西黎曼方程,人们就得到一个看起来非常简单的性质。
如果画一个封闭的圈圈,围绕着这个封闭的圈圈做积分,那么这个积分的数值仅仅取决于圈圈里面的拥有奇异性质的点,即所谓的奇点,奇点上函数变成无限大。
有了这个简单的定理,人们就开始到处去画圈圈了。
为了得到一个有效的数值,人们常常是这样画圈圈的
要么这个圈圈画成无限大,要么这个圈圈画成无穷小,要么在一条直线上来来去去。
例如我前面提到的欧拉发现的准阶乘函数,即所谓gama函数,人家是这样画圈圈的
从无穷远处开始往原点画直线,然后在原点附近画一个半径为无穷小的圆,然后再向着无穷大而去。
为什么要画无穷大,因为很多函数在无穷大处等于
0
为什么要画无穷小,因为很多函数在无穷小处等于0。
黎曼是一个非常善于画这种圈圈的人,有一日他凝视着欧拉发现的连乘连加公式,突然想到如果把这个欧拉公式中的一个量理解成复数会发生什么呢?
然后他就推开了解析数论的大门。
复变函数有一个魔法,它会告诉你
1+2+3+4+……=-1/12
1+4+9+16+……=0
1+16+81+256+……=0
第二个式子是1平方加2平方加3平方加4平方一直加下去
第三个式子是1四次方加2四次方加3四次方加4四次方一直加下去
第一个式子相信只要上过中学的第一眼看上去就觉得肯定不对,怎么可能正数加正数加着加着变成负数了
第二个式子和第三个式子也让人觉得不可能,怎么可能正数加着正数变成0了
但实际上复变函数论断言
所有的偶数次方,从1加到无穷大都等于0
这是为什么呢?
人们说互联网上啥都有,只要有问题就会有答案。
但很遗憾的是我搜索中文互联网,就没有几个答到了点子上,大都是牵强附会的回答。
实际上,要理解以上式子,就要理解复变函数的一个魔法叫做复函数的解析延拓。
在复函数中,一个函数的解析范围可以比另一个函数的解析范围大,而且在双方都解析的情况下,两者又都相等,那么这个时候,解析范围大的函数称为解析范围小的函数的解析延拓。
什么叫做函数的解析?
当一个函数加着加着变成无穷大了,这个函数就是不解析的,这个变成无穷大的函数是没有意义的或者说是发散的
回到前面的式子
1的-s次方+2的-s次方+3的-s次方+……
这个函数我们在前面介绍过了,是欧拉这个数学英雄发现它具有将连加变成连乘性质的名叫zeta(泽塔)函数即ζ函数
这个ζ函数在一般情况下只有s大于1才不会加着加着加到比任何一个数都大
即在一般情况下只有s大于1,这个函数才有意义。
但如果只能研究s大于1的情况,就没有黎曼后面的伟大的发现了。
黎曼发现,将上面的ζ函数变成一个积分,可以把这个函数变成一个在s更小很多的时候依然不会变成无穷大的函数,而且在s大于1的时候,两个函数又完全相等。
函数解析范围扩大,术语就叫做函数的解析延拓。
黎曼把ζ函数解析延拓成了什么样子呢
本人记性不好,记不住,只好拍照了
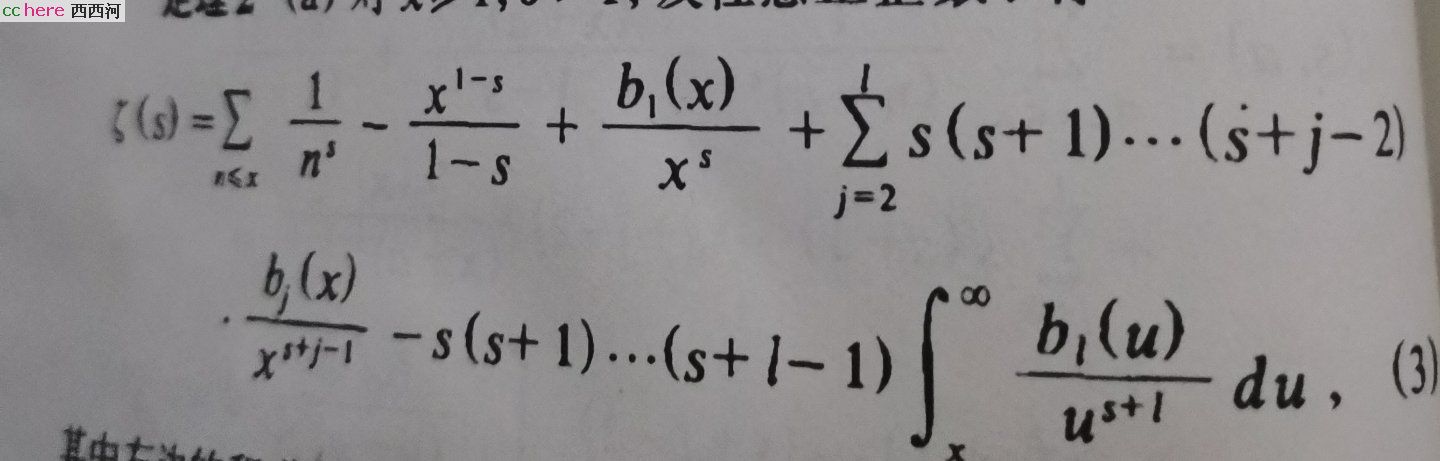
为啥1加2加3一直加下去变成负数了?
因为这里的1+2本来就不等于3这里的1+2其实就等于
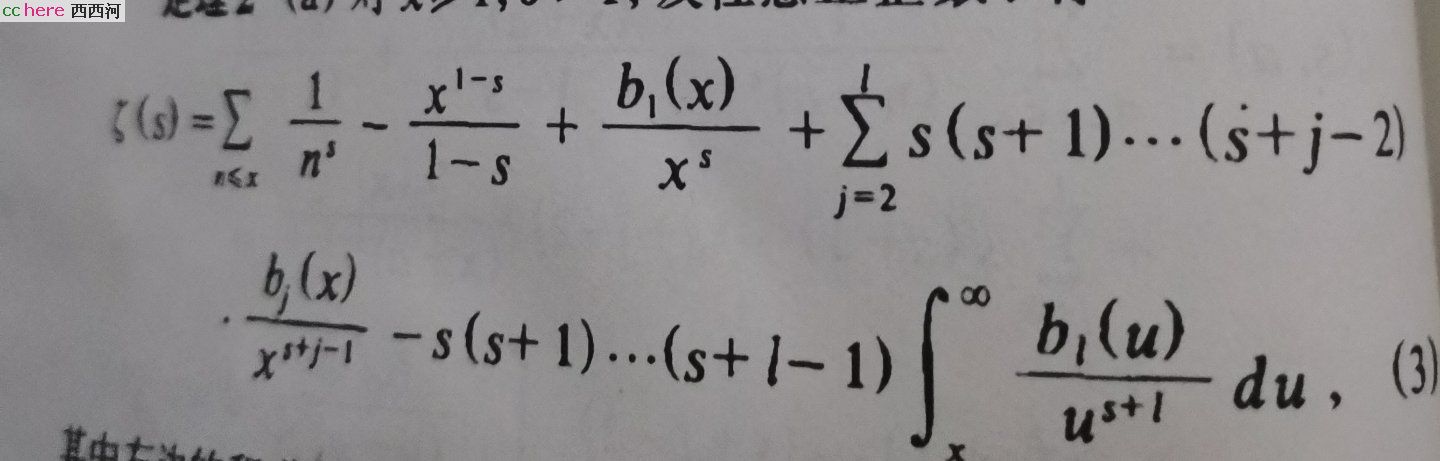
上面的式子中取x=2就是1+2的值,显然这个值不等于3
那么为什么要解析延拓呢?
因为我们需要把这个函数比较重要的点给圈起来,然后对这个圈圈做积分。
这个ζ函数有一个最重要的点是s=1这个点。
这个点是不管你怎么做魔术,ζ(1)都会比任何一个数都更大,即s=1是ζ(s)的极点,做积分的时候需要把这个极点给包进去。
把这个极点包进去了,就可以很显然的得到高斯——这个数学王子在此前就素数研究而得到的一个结论。
高斯曾经就素数个数给出过一个相当精确的估计,并且完败了勒让德。
高斯是怎么估计素数个数的,黎曼怎么证明高斯的估计的,且听下回分解。