- 近期网站停站换新具体说明
- 按以上说明时间,延期一周至网站时间26-27左右。具体实施前两天会在此提前通知具体实施时间
主题:【原创】兼整理,中庸考辩。 -- 铁手
所以说,这种说法还是比较形而上学的,不太符合科学认识论。之前看到一个视频是杨振宁还是丁肇中谈了这个问题,他大概也是这个意思。
您说的这个实际上是涉及到“无限”的辨析,《墨子》中对这个有很多论述,理论水平非常高,超越了古希腊(古希腊对无限是比较排斥的,一个无理数就被憋了2000年)。
比如下面这段话,
穷,或有前不容尺也。
穷:或不容尺,有穷;莫不容尺,无穷也。
说不论用有限的长度去量多少次,无限也量不完。这实际上和古希腊阿基米德公理(也叫阿基米德性质)相当。本质上是一样的。
但墨家认为在有限空间内无穷是可“尽”。
无穷不害兼,说在盈否。
无。南者有穷则可尽,无穷则不可尽。有穷无穷未可知,则可尽不可尽未可知。人之盈之否未可知,而必人之可尽、不可尽亦未可知,而必人之不可尽爱也,悖。人若不盈无穷,则人有穷也,尽有穷无难。盈无穷,则无穷尽也,尽无穷无难。
所以说阿基里斯是可以追上乌龟的,因为他只是落后乌龟一段有限的距离,而这段有限距离内即使有无穷多点但是“盈”的,因此“尽无穷无难”。
不知其数而知其尽也。说在问者。
不知其数,恶知爱民之尽之也?或者遗乎?其问也,尽问人,则尽爱其所问。若不知其数而知爱之尽之也,无难。
这里其实已经有了可数性(可列性)的思想,结合上文,可以推出墨家认为可数无穷也是可“尽”的。
这里墨家的反对方很可能是辩家(也称名家),因为从辩家二十一事和历物十事(均记于《庄子》)中有些论题和这里的诘问相似。尤其是这里提到了其中的“南方有穷而无穷”,但貌似在这个问题上双方的观点似乎是一致的。
墨家对“镞矢之疾,而有不行不止之时”的解答尤其精彩:
止,以久也。
止。无久之不止,当牛非马,若矢过楹。有久之不止,当牛马非马,若人过梁。
这里”久“通”宙“,指时间。这段几乎就是现代的”平均速度/率“和”瞬时速度/率“定义。而伽利略当年并没有提出这么明显”瞬时速度/率“定义,而是隐含在对加速度的讨论中。
其实伽利略之前就已经提出过十分类似的看法(一下摘自百度百科”平均速度定理“):
在14、15世纪,人们为这个关键定理提出了大量的算术和几何证明。其中以尼古拉·奥里斯姆的几何证明最为著名。这个证明大约于1350年提出,收在他的《论性质的构形》之中,这本著作对性质的张弛做了最富原创性的也是最完备的处理。
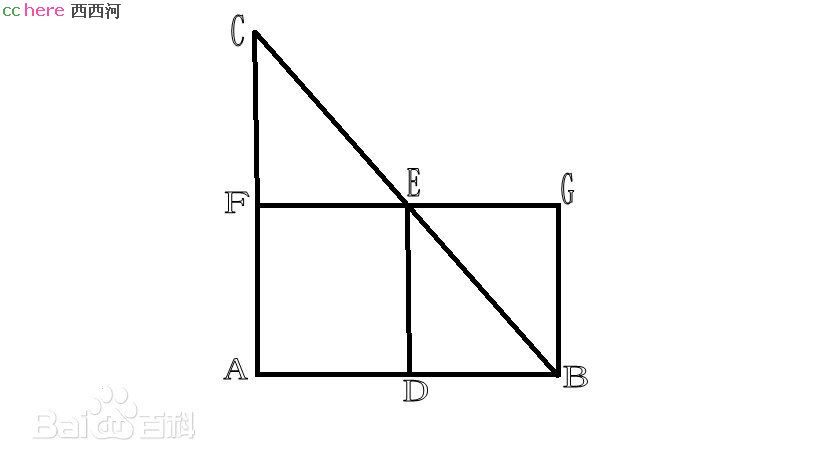
在图中,令线AB代表时间,垂直于AB的线段代表物体Z的速度:从静止点B开始,均匀地增大到最大速度AC。包含在三角形 CBA内的速度强度总量被设想为代表在总时间AB内Z从B出发沿直线BC到C所通过的总距离。令线段DE代表Z在沿AB时间中点测得的瞬时速度。现在,如果Z以DE处的速度匀速运动,在时间AB内从G到F沿线GF运动的总距离由长方形AFGB给出。如果能证明三角形CBA面积等于长方AFGB的面积,就证明了一个从静止开始作匀加速运动的物体所通过的距离等于在同一时间间隔内以匀加速运动时间间隔中点的速度作匀速运动的物体所运行的距离,即Z作匀速运动的距离S=1/2Vf t,等于Z作匀加速运动的距离S=(at^2)/2。
在14、15世纪的欧洲,尤其是意大利,平均速度定理的奥里斯姆的几何证明以及大量的算术证明广为认知。在伽利略《关于两门新科学对话》中,平均速度定律是第三天对话的头一个命题,伽利略的证明与奥里斯姆的极为相似,甚至所用的几何图形都一样,只是伽利略作了一个90°的转向。
明显看出《墨子》的定义十分直接,但西方确由于古希腊的影响喜欢用几何来说明各种代数和物理问题,十分的绕。到牛顿还是如此,直到实数理论完备才终止。
.
第二个是关于对半分这个问题,应该用开区间和闭区间做例子好理解。把一个线段分成两段,中间的点归哪边是要考虑的,所以只能分成一个开区间和一个闭区间,两者不完全一致。
实际上分法不只一种。”斫必半“说的是不多不少分成完全一样的两半,这是不可能的,如果放松条件的话还是可以分的。
如果不要求不多不少,在两种:
1. 加一个中点,可分成两个一样的闭区间。
2. 去掉中点,可分成两个半开区间。
如果不要求两半完全一样,就是你说的
3. 一个闭区间一个半开区间。
这三种方法其实都是可以的,#1对应的是波尔查诺的二分法,#3对应戴德金分割。现代实数理论基础中有七大定理,其中每一个都可以作为原理推出其余六个,其中闭区间套定理对应波尔查诺的二分法,确界原理对应戴德金分割,聚点原理和有限覆盖原理则用到了#2(有限覆盖原理其实和上面的”有限空间内无穷可尽“的思想是相通的)。
从以上讨论也可以看出西方数学实际上从古希腊到近代是绕了一个非常大的圈子,而中国的数学方向反而是一条直线直通近现代。
#2中如果去掉的不是一个点而是一个中电对称的线段(开的),那么对两边分别继续“日取其半”就得到康托三分集。
取一条长度为1的直线段,将它三等分,去掉中间一段,留剩下两段,再将剩下的两段再分别三等分,各去掉中间一段,剩下更短的四段,……,将这样的操作一直继续下去,直至无穷,由于在不断分割舍弃过程中,所形成的线段数目越来越多,长度越来越小,在极限的情况下,得到一个离散的点集,称为康托尔三分集,记为P。
- 相关回复 上下关系8
压缩 2 层
🙂极高明而道中用 1 冬晓 字33 2024-10-12 07:17:41
🙂墨子的这两番话说得好 3 pandaly01 字737 2024-10-11 02:24:34
🙂对墨子质疑“知之为知之”的这个问题,孔子有自己的答案 2 onlookor 字1456 2024-10-16 22:05:31
🙂实际上分法不止一种

🙂看这个康托三分和音乐的 1 大眼 字32 2024-10-16 05:11:56
🙂您说的应该是“三分损益法” 7 假设 字1976 2024-10-16 23:37:14
🙂音程若完美就不用练泛音技巧了 自由呼吸F0 字0 2024-10-21 22:33:19
🙂感谢假设兄说的那么详细, 3 大眼 字382 2024-10-17 20:42:21