主题:【原创】化工过程控制的实践 -- 润树
才看出些味道来!![]()
expotr model,应该是export model。看来是朱博士自己写的。这个公司好像也不大。
不过我很看好他走的这条路,就是将MPC简单化,规范化,程序化。另外自适应也是很好的方向。
自适应就是把辨识、控制器设计和实施自动化,想法是好的,但在实际上问题太多。想想吧,不要说自动测试,就是手工测试,我们要做多少事先工作?测试的时候要用多少力量来监测?事后要花多少时间分析数据?这些都自动化了,只能说明一件事:这些步骤已经高度程式化了,已经成为简单的重复劳动了,但这不是事实。对于简单的过程,这是事实,但这不是自适应系统的用武之地,也不是人们的期望。
人们对自适应的期望应用是:
1、显著非线性
2、显著时变
3、过程特性“无规则”变化(实际上是人们不知道变化到底是怎么来的)
人们的期望其实是不现实的:人工做不到的地方,期望自适应能创造奇迹,这好比人脑子想不明白的事,期望人工智能能想明白一样,是本末倒置了。
对于简单过程,trial-and-error并不是像想象中的那么落后,只要亲手做过几个回路,参数整定没有什么可怕的。一定要辨识、控制器设计这一套,就比较教条了。这和打仗一样,要是战场范围一目了然,敌情清楚,凭经验呼叫炮兵或者摆兵布阵就可以,不是一定要派侦察分队仔细标明敌情、沙盘演算才可以制定作战计划的。
就像你说的,对某些简单而又相对规范化的过程(比如发电厂),也许可以做出模式化,程式化的MPC。但简单的不见得就没有时变和非线性的问题。如果时变和非线性是比较快的反复变化,那自适应不太好用;如果是缓慢渐变的过程,像化学反应器由于催化剂的活性变化,裂解炉管道里的结焦等,那么由系统来进行一些模型自动辨识的工作,还是有可能成功的。对这些问题,工程人员事先当然应该都了解,暂时还不存在让人工智能来做人脑想不明白的事情;以后会怎么发展,现在也还不能断言。而且也可以考虑用别的方法去解决,自适应可以是其中的一种方法。总之是不期望它解决一切的此类问题,能解决一点,就算一点,然后再慢慢进步嘛。
我对由自动测试来获得的模型的有效性和其精度,其实没有很大的信心,甚至对手动开环测试而一次做出来的多变量模型,也要一个个想过计算过才放心一点,而且还要依赖在线闭环控制时的调试。这反过来说明,在线自动测试和模型识别值得尝试。在做一个MPC的项目时,毕竟会受到时间以及工厂生产状况变化的影响。而一但MPC投运后,有充裕的时间和在线数据来对模型进行反复辨识,以期找到更接近实际过程的模型。只是这个过程,依我看来,也还是需要有经验的工程人员的参与。
在我看来啥理论都没有必要,做个逻辑让控制设备像运转员(operator)一样, 开开阀门, 看看参数和目标差距, 再决定是继续开门,还是关门![]()
![]()
![]() ---太误事报
---太误事报
我还真就这样设计过控制逻辑, 而且在某电厂用着还不错,还拿了一个电力部的科学进步三等奖![]()
![]()
![]()
![]()
![]()
![]()
要是逻辑能够解决所有问题,我们这些搞控制的不就没饭碗了嘛?
要是光用逻辑就能控制的,一般说来控制水平不是太高的。逻辑的dead band不可能太小,要不然忙不过来了,所以控制精度不可能很高。
那是国产的阀门, 给小电流让它开它不开那种。
厂方没钱用于买进口的阀门,实在是自动化的脑袋+木头四肢,啥控制都做不来,只好模仿operator操作了
不过在国内的时候只纸上谈兵,还真是到了加拿大以后才练真把式。阀门不好真是头疼,但有时候工艺条件混蛋更头疼。我们有一个阀门,通过流量在300-400吨/小时,阀门压差在4-6MPa,通常开度在70-80%,但要求阀门的动作精度在0.1%以下,真是强求猪八戒绣花,头疼死了。这只是这个回路一半的头疼,在反应器开车的时候,流量可以在几分钟内改变50%,黏度从清水一样变到超过奶油浓汤,要是控制不好,反应当场就死了,然后背后站一排人,大眼瞪小眼地看着你,上头也是电话一个个打过来,头不大都不行。
鲜花已经成功送出。
此次送花为【有效送花赞扬,涨乐善、声望】
[返回] [关闭]
就是规模再小一点,但是流速的变化和对控制精度的要求,我们也很过分。
还好没有这么快的改变流速。
这个不仅要求对工艺流程极其熟悉,也要求相当大的计算工作,很多时候由于多变量的互相影响,事实和表面的逻辑完全相反-_-
能不能给我昨天的帖子http://www.talkcc.net/thread/1299517发表宝贵的意见啊?
谢谢啦!
在MPC一章里,出现了动态和静态优化的概念,也就是根据MPC的线性模型来计算过程最佳静态操作点和到达此点的动态途径。但是由于其模型没有全面地(MPC的变量只是过程所有变量的一部分)和准确地(忽略了过程的非线性)反映过程的特性,只能说它是一个片面/局部和近似的优化。
所谓过程静态优化(PSSO,process steady state optimization)则是一个远在MPC之前很久就出现了的古老命题:
给定过程的目标函数 J = f(x1, x2, x3, ……, xn),在x的约束条件下,找到优化变量x1, x2, ……, xn的值,使J最大化或最小化。
传统上,有两种方法来实现PSSO,一是通过过程的数学模型来计算(模型法),二是在线搜索(搜索法)。模型法中用到的模型,既可以是基于第一原理的机理模型,也可以是经验模型,或两者的结合,在MPC之前,大多是离线实现。也就是说,通过人工或计算机的计算,找到最佳静态操作变量的设定值,然后手动改变这些变量来实现优化。有了MPC后,PSSO所计算出的最佳变量设定值通过这两个系统间的接口传递到MPC自动实现。因此,PSSO可看着是位于MPC之上的一级控制系统。而在线搜索法则是直接改变优化变量的设定值,然后观察目标函数的变化方向,一步一步地去逼近最大/最小值。
最优化,从本质上说是一个数学问题,我们在高等数学中都学习过了。对于线性和低阶的目标函数和约束条件,可以用求导数和代数的方法来求解,而对于高阶和非线性的目标函数或约束条件,则需要用到更复杂的数学方法,像单纯型法,非线性最小二乘法(NLLS)non-linear least squre),分步二次规划(SQP,sequential quadratic programming),总体降梯度法(GRG,generalized reduced gradients)等等。MATLAB之Optimization Tool Box是用来求解此类问题的好工具。但这里我们不对这些数学方法作进一步的讨论,而将焦点放在过程优化的含义及其具体的工程实现。
我们先来看一个精馏塔。如图4.0.1所示,这个塔的操作目的是将进料中的二元主分Ca和Cb分离成塔顶的轻主分和塔低的重主分产品。一般地,这个分离过程是非理想的,即塔顶会有重主分杂质Xb,而塔底也有轻主分杂质Xa。现在的问题是,怎样的分离才算经济上最优。
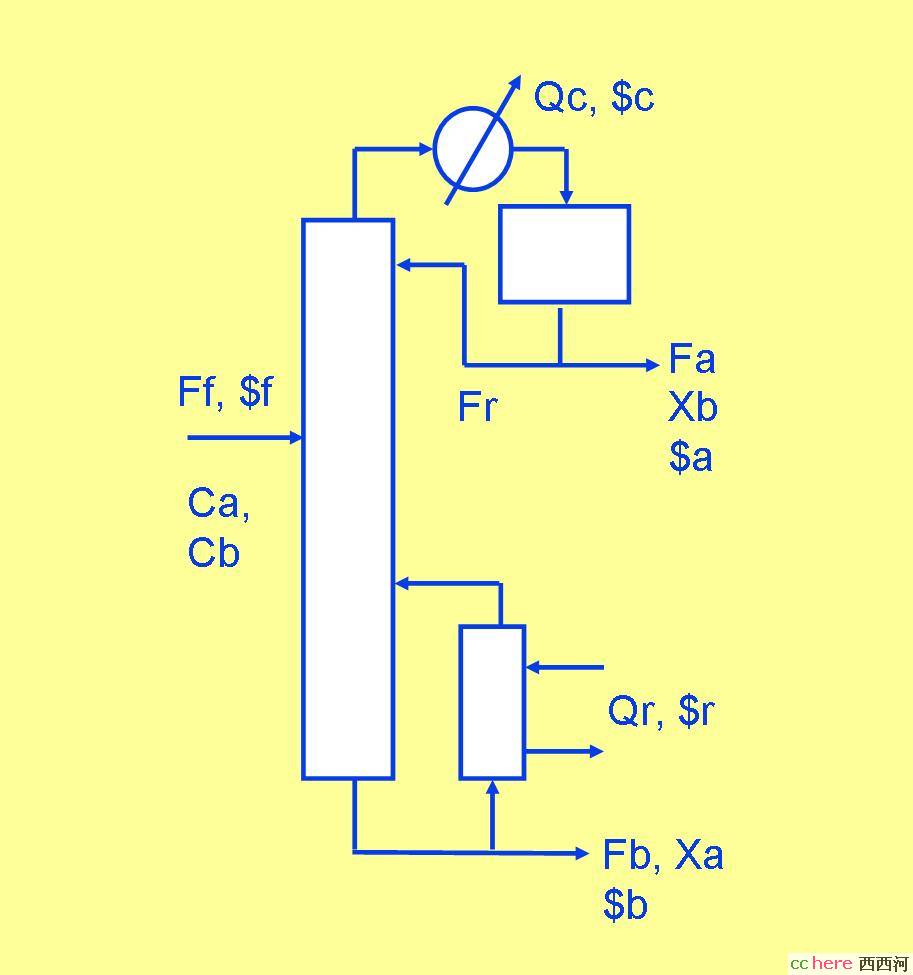
图4.0.1 二元精馏塔的分离示意图
我们可以定义这个过程的优化目标函数如下:
J = 产品所得 – 原料成本 – 能源成本
= Fa*$a + Fb*$b - Ff*$f - Qc*$c - Qr*$r (1)
式中,
Fa和$a – 塔顶产品流量和价格
Fb和$b - 塔底产品流量和价格
Ff和$f – 进料流量和价格
Qc和$c – 冷凝量和价格
Qr和$r – 再沸器热量和价格
约束条件是:
塔顶和塔底的杂质主分小于产品指标值 Xa <= Xa_spec, Xb<=Xb_spec (2)
冷凝器和再沸器能量受限于最大设计值 Qc <= Qc_max, Qr <= Qr_max (3)
由该塔的物料平衡,我们可以得到:
塔顶产品 Fa = Ff (Ca-Xa) / (1-Xa-Xb) (4)
塔底产品 Fb = Ff (Cb-Xb) / (1-Xa-Xb) (5)
对该塔的能源消耗,我们有经验公式:
冷凝量 Qc = Ff (c1 + c2*Xb + c3*Xb*Xb) (6)
再沸热量 Qb = Ff (d1 + d2*Xb + d3*Xb*Xb) (7)
将(4)-(7)代入(1),可得
J = f(Ff, Ca, Cb, Xb, Xa, $a, $b, $c, $r) (8)
在给定Ff, Ca, Cb, $a, $b, $c, $r的情况下,(8)式中只有Xa和Xb是优化变量,而如果塔底产品价格高于塔顶产品价格,即 $b > $a,那末Xa应控制在其上限(低价值组分作高价值产品),就是所谓的卡边操作。这样就只剩下唯一的优化变量Xb,可以很容易的算出它的优化值是15%,其对应的最大值J是$1006/小时。既然b主分价值高于a主分,为什么不尽量将这个数值控制在最小值呢?这是因为,要获得那样的结果,就需要加大回流量,导致冷凝量和再沸热量的消耗都上升,而抵消或超过由更多的塔底产品所带来的经济利益。图4.0.2是用MS Excell计算的图像显示。顺便说一下,MS Excell里的Add-Ins Solver也可以方便地用来求解复杂的优化目标函数。

图4.0.2 优化分离的图像显示
这个例子很间单,旨在用来说明化工过程中优化概念。实际的情形要复杂得多,我们将在下一节用Aspen Plus 的Real Time Modeling and Optimization来详细考察。
这里提出一个数学上臭名昭著的Banana函数优化问题,有兴趣者不妨用MS Excell里的Solver去求解一下。当然用其它方法也可以。
J = 100*(X2 – X1^2)^2 + (1-X1)^2
求解J的最小值,无约束条件。^2是平方算子。
在这里用不上了![]()