主题:【原创】电力系统漫谈 (一) 引子 -- 乃力
以从前跟系统外人士交流的经验,先说电网要在应对随机的负荷变化和设备故障情况下以一定的电压、频率运行,失稳就是电压、频率越限而且还不能挽回。再往下就是检修计划、备用安排、设备耐压载流水平等等了。功角失稳最终也可以体现在电压、电流、功率、频率超过设备承受水平上。至于静态、动态、小干扰这些的,说的是系统失去稳定的引发模式,不过抽象到数学和控制论、系统论的高度,所以听上去比较费解,一般都不会给那些人讲的。
系统失去稳定的最终表现还是因为电流过高,或者电压、频率过高或过低导致切机、切线路和甩负荷。美国几次大停电事故都是这样的。也许我可以专门写一篇介绍美国的大停电事故,特别是被广泛研究的1996年美国西部电网大停电。
NERC的问题,我的理解和你差不多,现在也不清楚它的权力到底有多大,值不值钱。它大概相当于过去的行业公会,但现在对行业内个电力公司的影响力可能没有那么大。它现在能做的可能也就是罚款,并不危及到电力公司的生存。真正说话算数的还是FERC(Federal Energy Regulatory Commission)和各个州的PUC(Public Utilities Commission)。他们在能源政策和项目审批方面的权力可以影响到电力公司的赢利、资产和股票价格等各方面。
在最开始曾介绍过,电力系统稳定性理论的研究从60年代末真正开始起步,经历波澜壮阔的30年,到上个世纪末突然陷入了困境。实际上,当时很多理论成果已经开始被应用于实际系统,也曾有过很好的表现。一些人已经开始了实时电力系统稳定校正性控制的研究,其终极目标是把电力系统建设成为一个具有自我监视、自我诊断、自我保护能力,甚至一定程度上可以自我恢复的系统。但电力系统的复杂性这个巨大的阴影,一直笼罩在研究人员和工程师心头。很多现场应用都是针对特定系统,甚至针对特定的系统状态。这不仅导致了应用成本非常高昂,而且因为分析过程依赖于太多的简化和假设,结果本身的可靠性也值得怀疑。终于,由于理论分析的成果不能在生产实际中进一步推广应用,使来自企业界的资金支持骤然减少。再加上电力市场改革吸引了绝大多数的注意力和经费,最终导致了电力系统稳定性研究几乎陷于停顿。理论与现实之间的差距,让众多为理论研究献身的研究者们黯然神伤。
但30年的理论研究对电力系统稳定运行的贡献还是巨大的。最主要的是,虽然在系统级的应用不成功,但稳定性理论研究促进了新型电力系统控制设备的使用,包括有功功率、无功功率潮流控制和发电机控制。这些设备如今被广泛地安装在各个电力系统中,对提高系统稳定性和系统输电容量起到了重要作用。另外,受过稳定性理论熏陶的电力工程师们在做系统分析时,有了更多的全局观念,能做到有的放矢,既提高了结果的有效性,也减少了盲人摸象式的时域仿真工作量。
电力系统稳定性理论的研究陷入低潮,但已有的理论成果并没有消失,也还有人继续努力。随着技术进步和基础理论(比如数学和控制论)的发展,也许有一天电力系统稳定性的研究会有突破。我自己算是知难而退了,但也会偶尔因为工作需要,翻一翻过去的笔记和参考书。每次,我都会在5分钟内产生头疼症状,然后开始昏昏欲睡。不过,我不得不承认,这些理论成果和很多其它学科的理论一样,虽然过程异常繁琐,但结果却能展现出来一种简洁之美。
电力系统是一个非线性的动力系统,并且可以进一步认为其结构参数是不随时间变化的。当系统中发生一个扰动后,如果假定在该扰动被消除后,系统的其它输入在暂态过程中保持不变,也没有其它事件发生,那么可以认为故障后的电力系统是一个自治系统(没有输入的系统)。自治动力系统在暂态过程中内部能量守恒。如果把动力系统的能量表示成动能和势能之和,那么自治系统的能量将在动能和势能之间进行转换。
说理论之简洁,如此复杂的电力系统暂态稳定,可以用一个在坑中小球的运动形象地表示出来,而且,竟然也可以从电力系统模型中推出几乎完全一样的公式。
这大概是一个初中物理的例子。先挖个坑,深度为h,再假设坑的内表面光滑无摩擦。然后,把一个质量为m的小球放在坑底。此时小球是静止的,动能Vk=0。小球相对于地面的势能是Vp=-m*g*h。势能也就是重力乘以做功的距离。现在,在坑底推小球一下,给它一个初速度v,也就是给它一个动能Vk=0.5*m*v^2,让它向上运动。当条件 0.5*m*v^2 > m*g*h 满足时,小球就会滚到坑外去,否则,就一直在坑里面呆着。如果考虑到坑内表面的阻力,只要小球不出去,最终会回到坑底。
图1 坑中的小球
用稳定性的语言来说,坑底对小球来说是个稳定的平衡点,坑就是它的稳定域,坑的边缘是稳定域边界,出去了就回不来了。
相应地,电力系统的正常运行状态是它的稳定平衡点。当电力系统受到扰动,如短路或切除大的线路或发电机等,会有暂态能量被注入到系统,相当于给了小球一个向上的动能。如果这个注入的动能被系统本身所吸收,系统是稳定的,反之系统将失去稳定。系统吸收注入动能的能力可以被理解为系统的势能。系统稳定与否,取决于注入的动能和系统稳定平衡点到稳定域边界之间的势能的差(类似于小球在坑沿和坑底的势能差)。
那个小球的能量是在我们熟悉的空间里计算的,其空间的度量是高度(或者距离),小球的速度是距离对时间的导数。电力系统稳定是在一个什么空间里呢?还得回到前面介绍过的 电力系统微分方程:
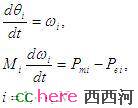
和小球-坑系统相比,电力系统的稳定性是被放在以发电机转子角度为度量的空间里来研究的。假如一个电力系统里只有一台发电机,也就是N=1,电力系统的动能和势能可以定义为:
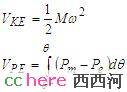
可以看到,电力系统的动能和小球的动能有完全一样的表达式,只是把速度换成了角速度。势能其实也是一样的,力在一定的距离上做的功,只不过此时的力是机械功率和电气功率的差,而且这个力是随着发电机角度的变化而变化。这也就是电力系统暂态稳定分析的基本公式,李雅普诺夫函数。因为具有能量的表达式,所以又叫能量函数。如果扰动注入到电力系统的动能大于系统自身具有的势能,系统将失去稳定。有了这个基本判据,剩下的工作就是如何计算机械功率和电气功率的差,以及如何找到稳定域的边界。
以前讨论过时域仿真是一个很耗时间的工作,往往需要仿真10秒甚至20秒才能判断系统是不是稳定,虽然系统失去稳定只需不到一秒。能量函数理论的意义在于,如果能通过某种方法找到稳定边界,我们可以在检测到系统轨迹越过稳定边界时就停止仿真而直接宣布系统失去稳定。另外,如果能定量或者解析地表示出系统的势能,可以在此基础上做进一步的分析,比如灵敏度分析等,有助于实现一些系统稳定控制。
理论已经把方向指明了,剩下的事就是八仙过海,各显神通,去寻找这个稳定边界。谁料,三十年弹指一挥间,稳定边界难过蓬莱山。
难在哪里呢?稳定边界本身对能量计算并不是最重要的,我们需要知道的是决定边界的那个点:不稳定平衡点。系统稳定运行点和不稳定平衡点之间的势能差,就相当于小球从坑底到坑沿的势能差,对系统稳定有决定意义。什么是不稳定平衡点,当成功地把削尖的铅笔,尖的一头朝下立在桌子上时,恭喜你,你得到了一个不稳定平衡点。突然一只蚊子从旁边飞过,铅笔倒了。那就对了,不稳定嘛。电力系统的不稳定平衡点也是一样,系统实际上无法在那里运行,只是一个数学意义上的点。糟糕的是,在这个平衡点附近,电力系统方程很难求解,换句话说,就是几乎抓不到这个点。想想也是,倒立铅笔的事情哪是那么容易干的。
本帖一共被 2 帖 引用 (帖内工具实现)
发点儿牢骚![]() 。
。
搞稳定计算,没有准确的基础参数,模型算法再好也没有用。最重要的发电机四大参数(发电机及其励磁系统、原动机及其调速器),往往由于设备分属不同经济实体,导致全网大范围测量工作开展困难,而且测量手段、计算方法、人员责任心等种种因素都会导致不同机组参数误差各不相同。从管理的角度上来看,反倒是欧洲、中国(以前)那种厂网一家的模式下,能比较好地进行这种工作。
其次负荷测量也是个大问题,电动机比重和分布能估算到多准?专家到这,有时候也是巧妇难为无米之炊。
数据的确是个问题。最重要的校验数据的机会反倒是大事故发生之后,反复对比仿真结果和实际记录的系统响应,对数据进行调整。发电机和电动机都是这样。另外,现在新设备层出不穷,模型的准确性也成问题。比如风力发电的动态模型。
前几年兴起的一个研究方向就是利用系统观测数据来倒推发电机参数。有一些文章问世,但还很不成熟,没人敢用。看来确实有必要换个角度看问题。也许PMU是个解决办法。这方面国内是领先世界的,不知道你有什么看法?
需要企业界的强大支持和研究者个人的潜心研究,系统工程兼长期工作。
现在国内前者好说,国家电网一心要搞大联网,稳定问题摆在面前,通过中国电科院在下大力气搞,仿真中心和建模测量工作都在开展中。这几年区域电网大扰动试验做了好几回了,电网振荡事故也出过一两次,问题是有没有人能耐得住寂寞好好分析分析那海量的数据。当然我们用PMU时间不长,数据同时性好像点儿问题,而且国内对GPS信号一直不太放心,换北斗的呼声已经出现过。
不过也不能全怪学术界,这几年电力大发展,电厂、电网建设速度在全世界都是最快的,电网结构变化太快,用两三年前的实测数据得出的结果,很难说有多大意义。从这个角度来说,反倒是发展几近停滞的北美电网,有条件好好搞一下。我记得95、96年WSCC大停电的时候,PMU的数据就已经有了。
整个系统的动态数据,特别是负荷这块儿,更新一次要好长时间。结果出来了,系统也变了。美国好一些,WSCC96年大停电以后,从直流模型到负荷模型都更新了一遍,现在还能凑和着用,因为系统没怎么变。
另外,全世界的电力系统都一样,搞数据的工作吃力不讨好,没有人愿意做。这也是个问题。
美国PMU安装得很早,但远远没有真正发挥作用,基本上是个摆设。96年那会儿应该有PMU数据了,但几个主要分析报告里都没有采用,最多也就是在最后提一下。现在号称PMU之父的Phadke教授都宣称PMU应用的希望在中国,建议美国电力公司的人到中国去参观学习。
一是你提到各种保护间的配合。如何配合呢?
二是时域仿真。这种肯定是极耗时间的,为什么不做频域的呢?频域计算有什么问题?
感觉能量函数的方法求极值有问题,要不干脆用电磁场理论,波动方程统一得了。
先说第二个问题。我不是搞控制理论的,可能理解的不对。我想可能主要是因为电力系统在暂态时严重的非线性使频域分析变得很困难。实际上早期曾有过这方面的研究,但逐渐都放弃了。不过,一旦可以线性化了,比如在电力系统小扰动稳定分析中,频域分析和时域分析(状态空间法)还是各擅胜场的。虽然状态空间法应用更多些,但有一个主要的电力系统特征根计算方法就是利用频域进行的。参数鲁棒性的研究也主要是在频域进行。
再说保护配合的问题。电力系统中有两大类保护,一种是设备保护,一种是系统保护。顾名思义一个是保护设备本身的,一个是保护系统的。配合问题就有设备保护之间的配合,系统保护之间的配合,以及两类保护之间的配合。这个配合又包括保护装置设定值的配合和动作时间的配合。
设备保护之间的配合相对简单。简单地说,就是如果被毒蛇咬了手指,争取做到最多只切除那个手指,而不用把整个胳膊都截了。当然,也不能左手被咬,反去切右手。(抱歉,有点儿血腥,不知怎地一下就想到这个例子)
系统保护和设备保护之间的配合例子也很多。系统中比较常见的一种系统保护是低频减负荷,就是频率太低的时候要甩掉一些负荷。而每个发电机都有一个保护装置,当频率过低时自动把发电机从系统中隔离。这两种保护如果配合不好,会雪上加霜。应该是低频减负荷先动作,使系统频率恢复正常,这样可能就不用切发电机了。如果是让发电机的保护先动作了,这个发电机是得到了保护,但系统频率会变得更低,不仅可能需要甩掉更多的负荷,甚至会导致其它发电机保护动作,直到系统垮掉。
有人这么做过。几年前我还真看过几篇用波理论分析电力系统稳定的文章,MIT的几个搞控制的教授写的。不过实在有点儿超出我的理解能力,具体内容已经没有什么印象了。
帮着在国内找一些当时停止电力市场转而做区域节能调度的分析报告。公开的报告就行,有内幕更好。最近整理一些电力市场的资料,想比较一下。先在此谢过了。
鲜花已经成功送出。
此次送花为【有效送花赞扬,涨乐善、声望】
先花谢了
再一次重新学习,加深理解。
自动理论在电力系统中的应用,还有很长的路要走啊。
麻雀虽小,五脏俱全的道理在电力系统并不总是适用。下面这一段介绍的最简单电力系统的稳定性分析并不能自动引伸到实际系统。但是,从这个小系统里,我们大体上能得到一些对大系统稳定的直观认识。照着猫去找老虎,虽然差得远了些,但还是勉强能和熊区分开的。
对暂态稳定研究来说,最简单的系统就是如下图所示的单机无穷大母线系统。中间是两条输电线路,一边是一台发电机,另一边是永远静止的无穷大母线。这个系统有些象在楼顶上挂个小气球,不管气球怎么随风而动,楼一般没事,最多就是气球飞上天了。
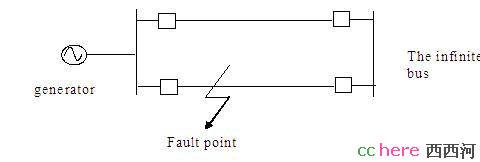
图1 单机无穷大母线系统
进一步假设,无穷大母线电压是V,电压相角是0;发电机母线电压是E,相角是θ;每条线路的阻抗是X。两条线路并联,阻抗就变成了X的一半,暂且用Z表示吧。对这样一个系统,发电机送出去的有功功率是多少呢?闲话少说,直接给出公式:
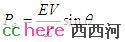
前一节提到过,计算能量函数除了需要找到不稳定平衡点,还要计算电气功率和机械功率的差。上面的公式就是单机无穷大母线系统的电气功率,是电压相角的函数。再考虑到系统稳定运行时,机械功率和电气功率相等,那么,
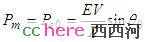
其中,θ0是系统稳定运行时发电机电压的相角。现在假设在其中一条线路上发生短路故障,发电机电压E瞬间减少到几乎是零(取决与故障点离发电机的距离),这时候发电机的电气输出功率也变得很小,但也可以用类似的正弦函数表示。在暂态过程中,相角会改变(想象一下,一阵风吹过,那只气球会怎么样?),但可以假设机械功率不变。如以前讨论过的一样,发电机这时候会开始加速。故障线路很快会被打开以清除故障,只剩一条线路运行,但电压回升,输出的电气功率也开始回升。因为线路的阻抗变了,发电机的电气功率此时变成了:
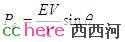
因为系统简单,电气功率能直接表示成是电压角度的正弦函数,我们可以把这些函数画到图上。这就是电力系统里著名的功角曲线。横轴是电压相角,纵轴是功率。水平直线是机械功率,三个曲线分别是对应不同状态时的电气功率。图中机械功率和横轴之间的两条长竖线,做左边的标识出了故障发生前的系统运行点,右边的则对应故障切除时的系统运行点。
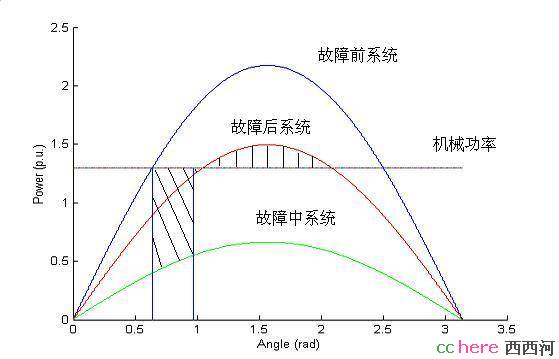
图2 功角曲线
大家不妨试一试把斜线阴影区域和竖线阴影区域的面积写成功率对相角积分的形式,看看会得到什么?
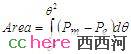
看着很熟悉吗?这是不是我们 前面看到过的势能呢?答案是肯定的,来比较一下势能的公式就知道了:
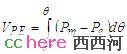
因为故障中的电气功率计算很不准确,计算斜线阴影区域的面积是没有意义的。所幸能量守恒定律再次给我们指明了方向。还记得那个坑底的小球吗?这次我们让它从左侧滚下来。球在坑底时的动能等于它在左侧开始下滚之前的势能。
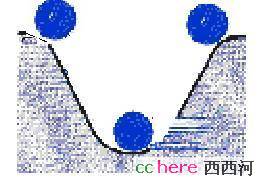
图3 滚落的小球
同样道理,在故障切除那一时刻的系统动能也正好等于斜线阴影区域对应的势能。故障切除时的系统动能前面也介绍过了:
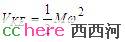
这样,斜线阴影区域的面积等于故障给系统注入的动能,竖线阴影区域的面积则相当于小球爬上右侧斜坡后具有的势能。如果这个势能小于球在坑底时的动能,小球将离开这个安乐坑。对这个电力系统来说,如果斜线面积大于竖线面积,就不稳定了。现在,判断系统是否稳定,变成了判断两个面积哪个更大。而这个判据正好和前面介绍的能量函数法完全等价。这就是学电力系统的人都熟悉的等面积法则。斜线面积又叫加速面积,竖线面积又叫减速面积。故障后系统功角曲线和机械功率的交点,左边的是稳定平衡点,右边的是不稳定平衡点。多么和谐,多么对称的电力系统!可惜,猫是猫,虎是虎。我们谁也不会抱个老虎坐沙发上看电视,是不是?
不管怎样,从这只小猫身上,我们还是能得到一些有用的信息。除了前面讲的以外,比较重要的有三点。
第一,是对一个给定的系统结构,在稳态时,其电气传输功率有个上限。对这个简单系统来说就是电压相角为90度(正弦为1)时的功率。
第二个是,输电系统的阻抗对输电功率上限有重要影响,阻抗越小,上限越大。怎么减小阻抗?要么缩短线路长度(也叫电气距离),要么加粗线路导体或几条线并联,要么用其它办法。什么叫其它办法?比如说,高压线路的阻抗比低压线路的小;再比如说,线路自身是个大电感,我们可以串联进一个电容,正负抵消。那超导行不行?
第三个是,增加稳态时输电功率的上限,可以提高系统的暂态稳定性。比如说,把功角曲线中故障后曲线升高的话,减速面积增大,系统也更稳定。这样一来,我们知道了一个增加系统暂态稳定性的方法:减少输电路径的电气距离。一个自然的推论就是长距离输电天然地不利于系统稳定。
本帖一共被 2 帖 引用 (帖内工具实现)
暂态失稳对电力系统的影响最严重,可以在极短的时间里造成系统解裂和大范围停电。在电力系统稳定分析里面,暂态失稳的分析和计算也是难度最大的。但往往越严重的事故发生的机率越小,真正让电力系统失去暂态稳定的大故障在系统中难得一见。随着系统规模越来越大,在单个发电机或发电厂发生的暂态失稳对系统的影响也越来越小。一旦专门的保护装置检测到失稳,可以迅速把发电机与系统隔离开。损失的功率可以由系统内其它发电机来平摊。与此同时,长距离输电越来越普遍,电力系统变得越来越象哑铃:两个区域通过若干条很长的输电线路联系起来。实践经验表明,这样的系统在受到微小扰动时,有可能发生两个区域之间的振荡。当振荡发生时,调度员可以看到系统电压、输电线路上的功率、发电机的输出功率等电气量围绕各自的中心线上下波动。有时候,这种波动会逐渐衰减,直到恢复正常;有时却可能越振越大,系统中的电流越来越大、电压越来越高或越低,直到保护装置把设备切除,并形成连锁反应。世界上有几次大停电就是这么造成的。
所谓的小干扰是相对于导致暂态稳定的大干扰而言,对系统冲击没有那么大。有可能是简单的线路开断,也可能是突发的发电机故障等。小干扰稳定要研究的目标主要是从系统中那么多发电机中,找出到底是谁在捣乱,以及如何有效制止。曾与一位教授聊小干扰问题。该教授在电力系统稳定性研究领域的地位堪称东邪西毒。我本想得到些武学密笈什么的,没想到,此公脱口而出:我认为电力系统工程师和研究人员还没有准备好去真正搞清楚小干扰问题。
了解该教授性格的人大概会有同样的第一反应,我当时也这样想,是您自己还没有准备好去真正搞清楚小干扰稳定问题吧!这样想,没有不尊敬的意思。一方面是因为该教授的性格圈内皆知。另一方面,主要是因为在过去30年里,几乎和暂态稳定研究同时,也有很多学者和工程师在小干扰稳定领域做了深入研究,其研究成果的实用化水平甚至超出了暂态稳定研究。
那什么是电力系统的小扰动稳定呢?一般地,是指在发生一个扰动后,系统并不直接失去暂态稳定,其时域仿真结果体现为在一个平衡点附近来回振荡。如下图所示。这是一个临界振荡的例子,可以看到几乎是个等幅振荡。这也可以用小球-坑系统来解释。当坑壁光滑无摩擦时,给小球一个初速度,只要不离开坑,小球将在坑里上上下下个不停。在实际中,这种无摩擦的情况几乎是不存在的,所以小球最终会回到坑底。实际的电力系统也有类似的摩擦,但沿用的是电路理论的概念,不叫摩擦了,叫阻尼。而且,这个阻尼可正可负。从基本电路理论可以知道,正阻尼使系统振荡幅度越来越小,最终回归到一个平衡点;负阻尼使振荡幅度越来越大,系统最终失去稳定。
电力系统小扰动失稳主要是因为在小扰动发生后,系统的拓扑结构无法提供足够的阻尼造成的。小扰动分析的一个主要结果就是计算系统振荡的阻尼。因为是小扰动,可以对由系统微分-代数方程组进行线性化,得到系统的状态空间,在此基础上应用线性系统的方法进行分析。线性系统的东西就不多讲了,挑简单的说一说。状态空间可以认为就是个代数里面的矩阵。矩阵理论也不多讲了,其核心内容之一就是计算特征根和特征向量(这个,理工科的同学都应该知道),这也是小扰动分析的第一步。因为电力系统的这个矩阵是非对称的,所以其特征根是复数,可以写成a+jb的形式。算出特征根和特征向量之后,就可以用线性系统理论进行稳定性判别了。当有虚部不为零的特征根时,系统在小扰动下会出现振荡;实部都在复平面虚轴的左侧(负数),系统是稳定的,阻尼为正,并且实部离虚轴越远,阻尼越大;如果有一个或多个特征根有正实部,系统是不稳定的,阻尼为负;如果实部为零,但虚部不为零,就是图1那个样子,等幅振荡,此时,不说阻尼为0,而是用一个新名字,叫极限环。
想想看,如果实部虚部都为0怎么办?
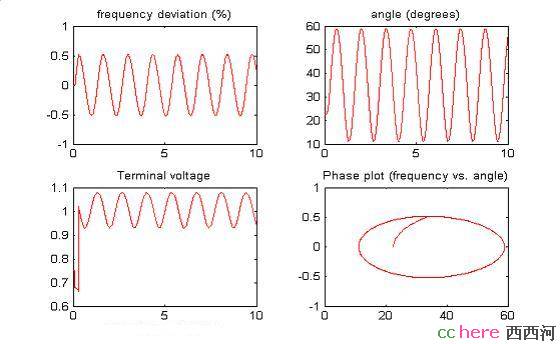
图1 系统振荡
好象没法办了。出现零特征根,矩阵奇异,系统在数学上已经没有解了。但在非线性系统里,什么都可能发生,别有洞天也说不定。
以上是在线性化的状态空间上的分析。众所周知,电力系统是个非线性系统。那这样的线性化分析可以吗?大多数情况下是可以给出足够好的结果的。但毕竟是非线性系统,线性化的分析结果只能是近似解,很多非线性系统的特性并不能完全在线性分析中体现出来。为了深入挖掘电力系统稳定性,特别是小干扰稳定的根本性质,各种眩目的非线性系统理论也被纷纷应用到电力系统,比如分岔理论、混沌理论等。前面那个教授的意思实际上就是在这个非线性分析领域,人们还没有准备好。这一点上,他是对的。原因嘛,还是系统太大太复杂,很多现象还没有能够有很好的解释。比如看图说稳定(续)中的那个振荡。那篇论文的作者给出的解释是系统中有两个极限环,大环套着小环。当振荡中系统某些设备状态变化时,激发了系统运行点在两个极限环间的跳变。
但在工业界,基于线性空间的特征根分析确实取得了很好的应用成绩。通过特征根分析,电力工程师可以预见到系统振荡(可观),并知道如何采取措施避免发生振荡或知道什么样的扰动更可能引起振荡(可控)。下面给个小扰动分析的案例。
大家都知道,智利这个国家细长,4,300公里长,平均175公里宽。这决定了它的电网也是一样。智利的电力工程师很早就发现他们的系统会偶尔发生振荡,特别是南部和北部地区的发电机之间的振荡。90年代,他们用西门子公司的小扰动分析软件包对系统进行了分析,得到的结果令人鼓舞。反映系统可观性的右特征根明确指出了振荡主要发生在南北两组发电机之间,这和他们的运行经验是一致的。令他们兴奋的是,反映系统可控性的左特征根还给出了另外一个亦喜亦忧的结果:系统最薄弱的环节在连接南北两个发电机群的细长输电网的中部。就是说,如果在中间发生一个扰动,会最大程度地激发系统的南北振荡。搞电网规划的工程师得动脑筋加强那个地方的电网了,因为那里是他们系统的七寸。
说到底,小扰动分析的核心是特征根计算。其难度主要在于系统规模太大。比如,一个大的互联电网,可能会有20000个节点,8000个发电机,其状态空间的维数将有可能达到十几万甚至几十万。在上个世纪80、90年代,三个研究小组分别独立地在这个领域做出了重要贡献,基本上解决了这个难题。一个是加拿大的PowerTech Lab (现为独立的软件和咨询公司,曾隶属于加拿大BC省水电公司),其关键人物是著名的Dr. Prabha Kundur和来自中国的汪磊(音)博士;一个是巴西的电力科学研究院(CEPEL)Dr. Nelson Martins领导的小组;另一个是德国西门子公司,当时的核心研究人员是同样来自中国的王小波博士。除了巴西的小组,另两个小组里起关键作用的都是我们中国人,这是很值得我们中国的电力工程师自豪的事情。
本帖一共被 1 帖 引用 (帖内工具实现)