主题:【原创】冤假错案的数学原理 -- 同人于野
这是冤假错案的数学原理背后隐藏的问题。老瓦厉害![]()
江湖风传吴副总理曾对手下曰过:把你们全毙了有冤枉的,把你们隔一个枪毙一个,肯定有漏网的。这个就是不枉不纵不可能做到的最好说明![]()
只要判案/检测就必然有冤案(虚警)也有漏网(误警),这判案的尺度抓在哪里,要看虚警和误警造成的代价大小。最近河友朱百山的走向胜利系列就有一个例子:
王孩说:“是正规部队,来找区政府要粮食的。”
说着就来到哨兵面前,敌人扑上去,把哨兵和王孩捆起来,嘴塞住。区政府和区队的同志们正在睡梦中,被敌人包围了。敌人的机枪,冲锋枪,步枪对着前后门窗疯狂扫射。过后敌人蜂拥而上,冲进屋里。
区政府和区队共有四十一人,有三人因故不在队,还有三十八人。牺牲二十一人,被俘十六人,还少一人。
一人叛变,牺牲二十一人、被俘十六人,可见在战争环境里误警的代价特别大,所以审查倾向于降低漏警。但付出的代价是冤杀的可能超过和平环境。最终付出的总代价是叛徒漏网的造成损失和冤杀造成的损失。
C(漏网)*P(叛徒通过审查) + C(冤杀)*P(好人未通过审查)
误警代价C(漏网)越大,为了降低总的损失、为了整个组织的生存和发展,审查的门限就越严格,付出的代价就是冤案![]()
革命,确实不是请客吃饭,只有最坚忍的人才能走过来![]()
如果你真懂概率,你会想到要使用贝叶斯定理,然后你会发现这道题还缺少一个关键信息:那就是一般人感染 HIV 的概率。现在已知一般人感染 HIV 的概率是 0.01%,也就是说一万个人中才有一个人感染这种病毒。根据以上信息,这位不幸被检测为 HIV 感染者的朋友真有 HIV 的可能性是多少呢?
万分之一的感染率太离谱了吧。地球上60亿人只有60万HIV感染者?
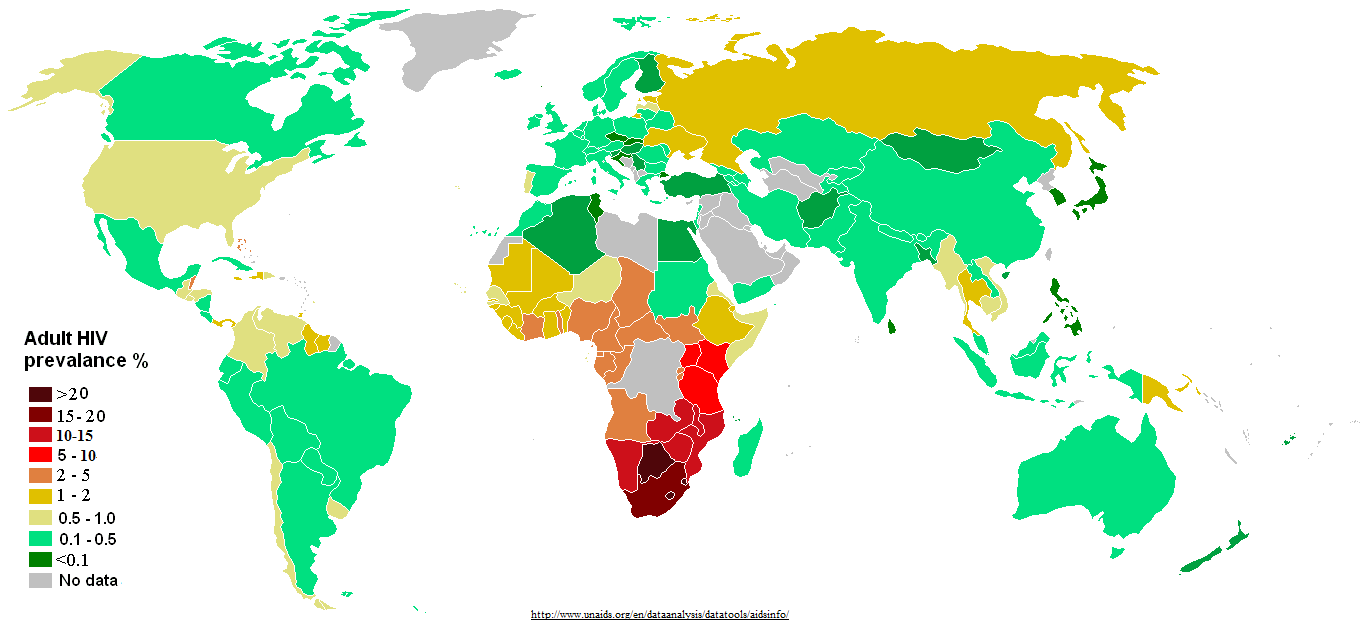
http://www.cdc.gov/hiv/topics/surveillance/resources/slides/2007report_tables/slides/HASR_19.pdf
开始看前两个例子还是蛮有趣的,最后那个抓特务的例子怎么看怎么觉得不对劲,完全是用统计学去生搬硬套的解释社会问题。
前两个例子能用贝叶斯定理是有条件的:已知 P(A) 和 P(B|A)。抓特务的例子,难道你知道社会中特务的比例和鉴别特务的准确率?
你的意思是鉴别特务的准确率很低,不管社会中特务的比例多大(当然不可能很大),抓特务必然是一大堆冤假错案。
“最好的办法是冒出来一个抓一个”,呵呵,等特务冒出来,损失就大了,补救都来不及。
社会问题还是用社会学的理论去解释吧。
本帖一共被 1 帖 引用 (帖内工具实现)
"宁可错杀一千"是追求高sensitivity。
无罪推定是追求高specificity。
有趣味,涨知识,能启迪。
这样的文章才是西西河的特色所在。
你的formula 还差一个关键的资料,所以无法计算出来,
那个0.5是不正确的哟~~
想算这个概率,有两种方法,一个比较理论(也就是同人于野兄的方法)
还有一个直白一点,列表
设 I 为 indicate
Ic 为 not indicate
H 为 有 HIV
Hc 为 没有 HIV
-----------------------------
I Ic
H
Hc
-----------------------------
已知 H 为 0.01%, 所以:
-----------------------------
I Ic Sub total
H 0.01%
Hc 99.99%
Sub totoal
-----------------------------
又, 现代技术检测 HIV 病毒的准确度已经到了惊人的程度。如果一个人真是 HIV 阳性,血液检测的手段有 99.9% 的准确率
换成统计符号,就是 Pr(I|H) = 99.9%, 换句话说, Pr(Ic|H)=0.1%
而我们知道 Pr(A|B)=Pr(A & B)/Pr(B)
所以 Pr(I&H)=99.9%*0.01%=0.00999%
同理, Pr(Ic & H) = 0.00001%
见下表:
-----------------------------
I Ic Sub total
H 0.0000999% 0.0000001% 0.01%
Hc 99.99%
Sub totoal
-----------------------------
用同样道理 Pr(I|Hc)
-----------------------------
I Ic Sub total
H 0.00999% 0.00001 0.01%
Hc 0.009999% 99.99%
Sub totoal 0.02% 99.98%
-------------------------------
0.00999%/0.02%=0.4995=50%
第二种方法是按照你说的方法计算, Baysian's formula
如下:
there are Ai, i=0......n exclusive sets,
A1, A2, A3,....An
Pr(Ai|B)= Pr(B|Ai)*Pr(Ai)/(Pr(B|A1)*Pr(A1)+Pr(B|A2)*Pr(A2)+....+Pr(B|An)*Pr(An))
晕了么....呵呵,在我们这里就是:
Pr(H|I)= Pr(I|H)*Pr(H)/(Pr(I|H)*Pr(H)+Pr(I|Hc)*Pr(Hc))
我记得概率课本上第一个有点意思的例题即是这个了,哪怕是医用概率也会上这东西吧,那个调查是不是揭示了德国的大夫不靠谱啊,嘿嘿
就是没干过易感的事的人群中,所以说你自认为没干过什么事,也没输过血,检测结果阳性的准确率是一半。
他漏了下面一段:如果你处在易感人群中,这检测结果阳性的准确率就极大地提高。
第一次是阳性,再查一次不就可以确诊了么
第二次阳性确诊的概率:P(A)~=0.5,P(A|B)=(0.5x0.999)/(0.5x0.999+0.5xE-4)~=1
所以按统计学原理,只要先拉网式排查一下,再对网里的仔细甄别,不就可以基本杜绝冤假错案了么。实际上也是这么操作的吧,先拘留,完了在起诉,然后一审,上诉,二审……
你这个算出来的结果看起来很惊人,其实是假设一锤子买卖,模型建的可是有问题呀,呵呵
0.01%应该是每年新感染率.
鉴别特务准确率再高也会是冤枉多的
多次检测的确可以提高检测的准确率,但要用你的概率模型来算,有个基本假设就是要两次检测是独立事件,这个假设事实上是不成立的。生物测试的误差有两方面,一方面是随机误差,这个可以通过多做几个replicates来校正;另一方面是系统误差或者说是实验偏差,就是所谓的intrinsic bias,这个是由测试技术本身所决定的。无论你做多少次检测,只要你没有改变测试技术,那些测量值都是相关的,而误差的平均就反映了这个实验偏差。所以多次确诊可能会提高检测的准确率,但提高的程度并没有你推导的那么明显。而即使改变了测试技术,两次测量值也未必是完全独立的,因为两种不同的测试技术也可能有相关性。很多所谓的不同测试技术只是在某些步骤上有所不同,而那些相似的步骤仍然存在共同的试验偏差。
一个单位,总是有5%的坏分子,这是个指标,搞运动就是要把那些混在人民群众里的5%的坏蛋抓出来。
这就说明领导同志对于这个被噎死概率是非常精通的。在发起运动时已经给出了5%的先验概率,给之后的革命行动指引了方向。
改选2/3,不改选1/3