主题:说一下贝叶斯公式 -- 天空不空
发病率高的病,和发病率低的病,对于sensitivity和specificity的精度要求差很多。比如艾滋病发病率很低,所以需要假阴性足够低,假阳性多一点没关系。
新冠的发病率也算不上高,再加上传染性强后果恶劣,真正需要保证的是假阴性足够少,假阳性的问题可以用多次检测解决。说实话,假阴性只要能降低到0.001%,假阳性就算是40%也比两个都是1%的检测方法好的多。
我第一个例子确实隐含了一个假设,即对健康人口,与患病人口的检测准确率是一致的,都是99%。
而您的例子中,估计在实践操作中也是,这两个准确率是不一样的。
实际上,在试剂上市前,肯定也要测,测试的结果有几种可能性:
1. 已知是病人,检测有真阳性
2. 已知是病人,检测有假阴性
3. 已知是健康人,检测有真健康
4. 已知是健康人,检测有假健康
出现假阴性,与假健康,两者概率是可以不一样的。
我这个理解,应该没错吧?
假阳性有其他渠道解决,让假阴性散落在社会上,才是最大的隐患
Good goo study
Day day up
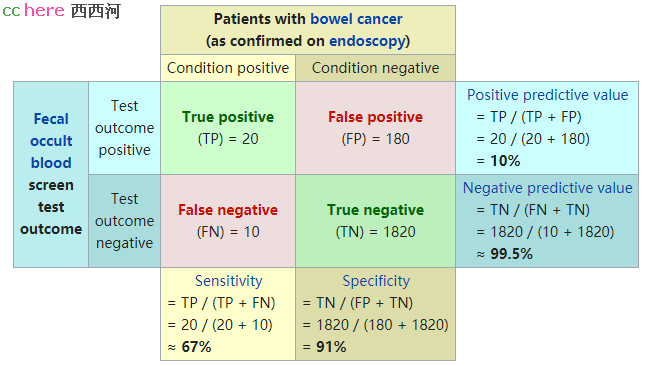
如果是accuracy。假设新冠的发病率是1%,那检测100个人,假设有一种试剂对每个样本都检测为阴性,那样的话它的准确度(accuracy)也有99%。可实际上这个试剂是完全没有指导意义的。
你假设的“‘准确度99%’的检测盒,100个阳性,1个错检测出阴性结果,100个阴性,1个错检测出阳性结果。”实际上是不成立的,我估计也没有这么高效的试剂。
我猜测可能会和F1 score有关系。
这明明是一个技术帖。普鲁托同学用数学公式把楼主同学的意思表达了。这个公式的长处在于一目了然。短处在于过于简化。但这个简化是数学本身的特点。
你偏听出弦外之音了。
斗争弦绷得太紧。![]()
就是正反测试误差对社会的效应是不同的,假阳性可以用隔离待查和再查一次来处理,对社会的影响很小,几乎可以忽略,假阴性的问题非常大,这个假阴性几乎导致今天西方社会防疫的全面崩塌。
中国对于假阴性的病人还会测CT,对于密切接触者还要隔离14天,这样的方法才能真正切断传染链。
将来西方哪怕到了70%以上的人感染过,如果不采取类似措施,面对输入性病毒感染,人群的偶尔集聚,还是会再次爆发疫情,最后到达全社会人人感染的局面。
说实话,我岁数不小了,人也胖,估计危险性不小,我对这种政策深恶痛绝。
还是那个假设:
1、试剂盒的敏感性为x
2、试剂盒的特异性为y
3、发病率为z
那么,一个检测为阴性的人,真正没得新冠的概率P是:
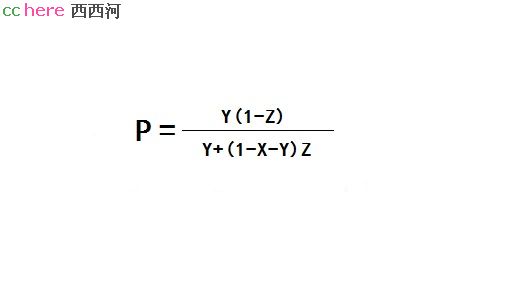
也可以看出,敏感性x越高、发病率越低,概率P越大。所以,技术部门提高试剂盒的敏感性、摸排出发病率是要务。
============
回到那个50%的话题:
当准确度为 90%,发病率为 90%;
当准确度为 80%,发病率为 80%;
当准确度为 70%,发病率为 70%;
............
在这些情况下,一个人检测为阴性的人,真正没得新冠的概率只有50%,这又是在抛硬币![]()
---------------
现在就是这样,不整点稀奇古怪、超出大家直觉的结论都不好意思说自己在科普![]() 。不但读者不感兴趣,小编也不喜欢,总要暗示作者加点料。
。不但读者不感兴趣,小编也不喜欢,总要暗示作者加点料。
PS:楼下燕人同学说俺太过简化。也是没办法,推导过程太多、等式太多都会降低可阅读性。
楼主和你的定义很清楚。假设条件也说明了。
还有异议,真出乎我想象。
算法是这个算法,做统计学的科普例子很好![]() 。但是拿这个数字说服大众不做大规模测试就错了,普兄没有这个意思,额不是指的他,而是之前不推荐戴口罩,现在又不建议提升测试量的所谓科学家。
。但是拿这个数字说服大众不做大规模测试就错了,普兄没有这个意思,额不是指的他,而是之前不推荐戴口罩,现在又不建议提升测试量的所谓科学家。