主题:说一下贝叶斯公式 -- 天空不空
看了一下高中三年的那个帖子,https://www.talkcc.net/article/4518147,顺便说两句
我知道河里有很多专业人士,但我还是想说一下贝叶斯公式,尤其是跟新冠的统计疫情有关的
众所周知,感染新冠并不必然检测出阳性,检测出阳性也不必然代表感染新冠,都是一个概率的问题,简单的说,就是,用A表明检测阳性事件,用B表示感染新冠事件,P(B|A)表示在检测阳性时感染新冠的概率,P(B)表示感染新冠的概率,P(A|B)表示在感染新冠的情况下检测出阳性的概率,P(A)表示总体样本中检测出阳性的概率,那么根据贝叶斯公式,举例说明,假设新冠的发病率为6%,P(B)=0.06,新冠病人检测出阳性的概率为99%,P(A|B)=0.99,如果检测一万个非新冠病人,有200个阳性,那么非新冠患者检测出阳性的概率为0.02,P(A|非B)=0.02那么总体阳性的概率P(A)=P(B)*P(A|B)+P(非B)*P(A|非B)=0.06*0.99+0.94*0.02=0.0782,在检测出阳性的情况下可以确诊为新冠的概率为
P(B|A)=P(B)P(A|B)/P(A)=0.06*0.99/0.0782=0.76,也就是检测出阳性时有四分之三的概率为新冠患者,但如果检测一万个非新冠病人里,有500个阳性患者,那么这个数值就变成
总体阳性的概率P(A)=P(B)*P(A|B)+P(非B)*P(A|非B)=0.06*0.99+0.94*0.05=0.1064,那么
P(B|A)=P(B)P(A|B)/P(A)=0.06*0.99/0.1064=0.56,也就是说此时检测养性是时感染新冠概率就只有二分之一左右,简单的说,感染新冠的概率既跟新冠患者中,检测出阳性的概率有关,也和非新冠患者中检测出阳性的概率有关,所以单纯看新观患者中检测出阳性的概率,是没办法得到检测出阳性时,感染新冠的概率,这段说的有点绕口,大家可以仔细体会一下。
一个人去检测新冠(抗体或核酸),结果呈阳性,那么他真正得新冠的概率是多少?需要什么数据、怎么计算?其实模型不复杂,以楼主所列贝叶斯公式主打,俺来简化一下![]() :
:
假设:1、试剂盒的敏感性为x
2、试剂盒的特异性为y
3、发病率为z
根据贝叶斯公式可计算,被查出阳性者真正得新冠的概率为:
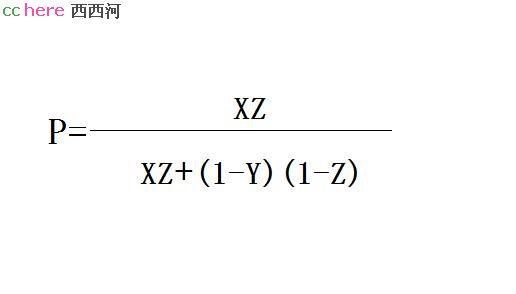
可以看出,特异性y、发病率z越高,概率P越大。所以当务之急是提高试剂盒的特异性和摸排出新冠的发病率。
======================
高三河友帖子中提到的是特例,可以列出一大组数据得到同样的结果。暂把特异性和敏感性笼统地称为准确度。
当准确度为 90%,发病率为 10%;
当准确度为 80%,发病率为 20%;
当准确度为 70%,发病率为 30%;
.........
这些情况下,一个人即使查出阳性,他真正得新冠的概率只有50%,简直就是在抛硬币。
这看起来很不科学,但科学就是这样![]()
假阴性比假阳性更重要,假阳性无非就是浪费了医疗/隔离资源,假阴性才是真正的社区传染源。无论如何,大规模排查相当于减少了传染源,使其更容易控制。这个所谓的50%的概率的逻辑和戴口罩没有用的逻辑是类似的
白宫那专家只是举例,检测手段“准确度”是本人的措词,记得专家原话是“99% specific”,不晓得专业上是什么定义。
反正是举例,瞎假设一个,阳性结果=感染病毒,阴性结果=没感染,“准确度99%”的检测盒,100个阳性,1个错检测出阴性结果,100个阴性,1个错检测出阳性结果。100万检测者,1%的感染率,实际含有1万个感染者,99万没感染。用这个99%的检测盒检测这100万个人,结果将检测出来9千9百个真病人,9千9百个假病人,真假一半一半,而另有100个真病人漏网。如果人群感染率不是1%而是0.1%,那检测结果更离谱。
专家的话只说一小半,更核心的意思是,不能无把关地大面积检测,尤其是初期人群中的感染率很低的时候,必须由医生决定谁该不该检测。
你说的这种是只有一种检测手段的时候,比如单一的核酸检测,如你所说,检测出9900个患者和9900个健康人,那没关系,再对这9900*2的人群抽血,查白细胞,淋巴细胞,血气分析,照传统ct,哪怕一种检测手段误诊的概率是50%,连续十种独立检测手段的误诊概率就变成千分之一了
主贴的贝叶斯公式解释的很清楚了
但是,这种问题存在于只存在单一检测方式的时候
一旦发现假阳性,结合上病史流调/CT/抗体检测,几样一结合,就可以测的非常准
只用抗体检测发抗体护照对于单次检查的个人是不靠谱的
但是核酸检查普查是很靠谱的,因为核酸PCR的特异性极高,接近100%,PCR检查几乎不存在假阳性,PCR的问题是敏感度低,假阴性不低,所以会漏掉不少无症状的人。但是挑出一个是一个,并且新冠病毒一旦传染,经常是聚集性传染,一发现基本是一个小集群,1。这种普查对武汉人的信心有意思,2。这种普查具有很大的科学意义。
这是湖北那边物资充足/检测能力充足的自然选择。海外连实际被感染的人都检测不过来,那是做不了普查。冰岛好像搞过一次类似的,冰岛总人口也才30万。
可是我们检测武器很多啊,流行病学调查/问诊/血检/抗体/CT
并且新冠病毒传染性极高,一例阳性经常带起一个小集群
这些方法一结合,就可以确诊或疑似隔离起来,大大降低传播风险
是我见过,最容易理解贝叶斯公式的例子了,不敢私藏,给大家看看![]()
![]()
![]()
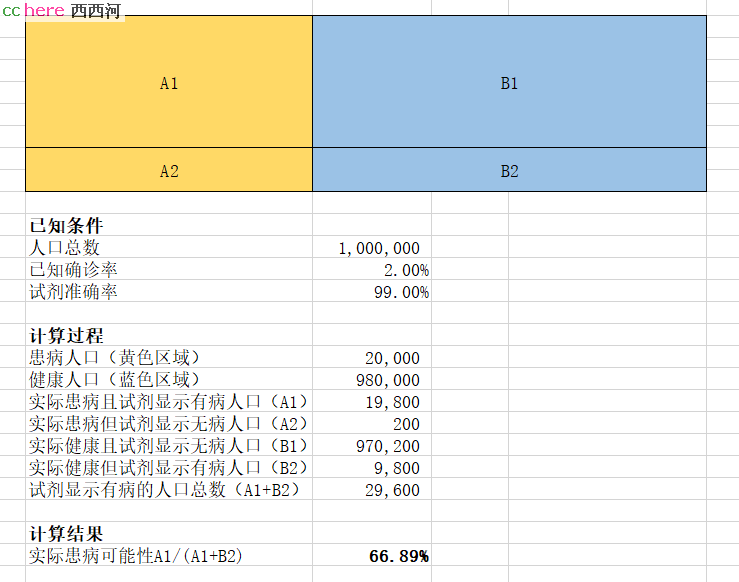
按照你的例子,我加多一个人口的数字,整个过程就很容易理解了![]()
![]()
![]()
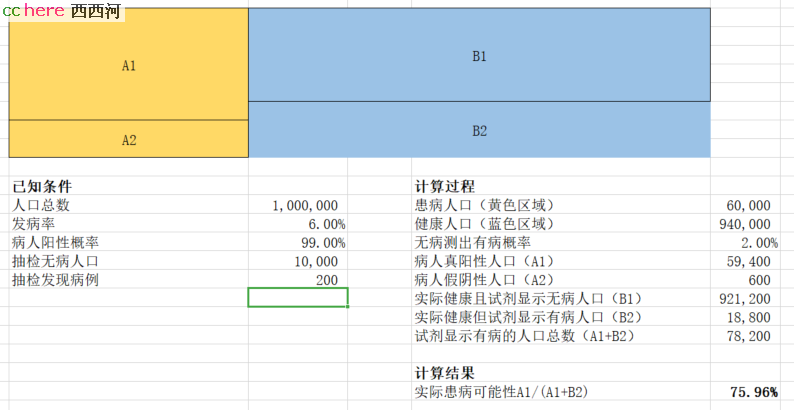
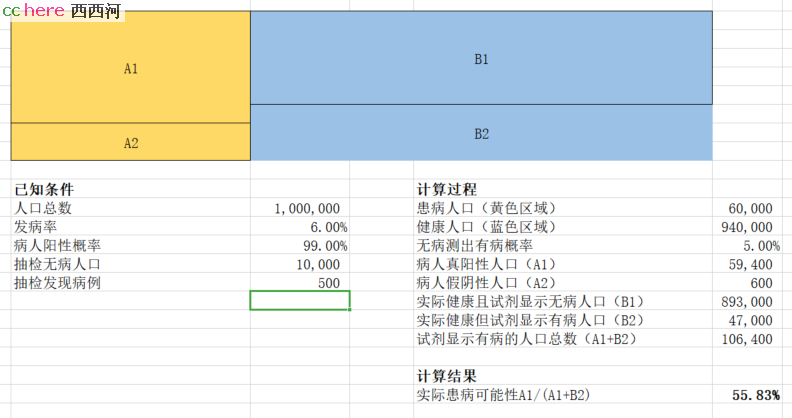
如果我算错了,也请指出。
问题还是出在试剂的准确率那里,同样的试剂,一百个病人里检测出99个阳性,并不代表在一百个健康人里一定就检测出一个阳性,也可能能检测出三个阳性,五个阳性,这句话的意思就是(假设S=健康人阳性率+病人阳性率,则S并不必然为1,也可以为1.02,1.04或者其他值)
这么说吧,理论上病毒A可以让检测试剂呈阳性,虽然100个病人当中都带有病毒A,但在实际检测中由于种种原因,只有99个病人的检测结果呈阳性,但除了病毒A,细菌B也可让试剂呈阳性,如果健康人携带细菌B的概率为50%,那么健康人中检测阳性率就是49%,这样病人阳性率+健康人阳性率就是148%,这个例子举得极端了一点,最理想的试剂当然是只对病毒A起反应,对其他生命体都没反应,但实际上这种情况很难,人体太复杂了