主题：阿波罗尼奥斯问题-Prob. of Apollonius -- 理性网民

如图，已知圆O及圆外一点P。过P点做直线与圆O相交于A、B两点。过P点做直线与圆O相切与C点。我们将证明三角形PAC与三角形PCB相似。因为这两个三角形共有一个顶点P，所以我们只需证明∠PAC = ∠PCB。

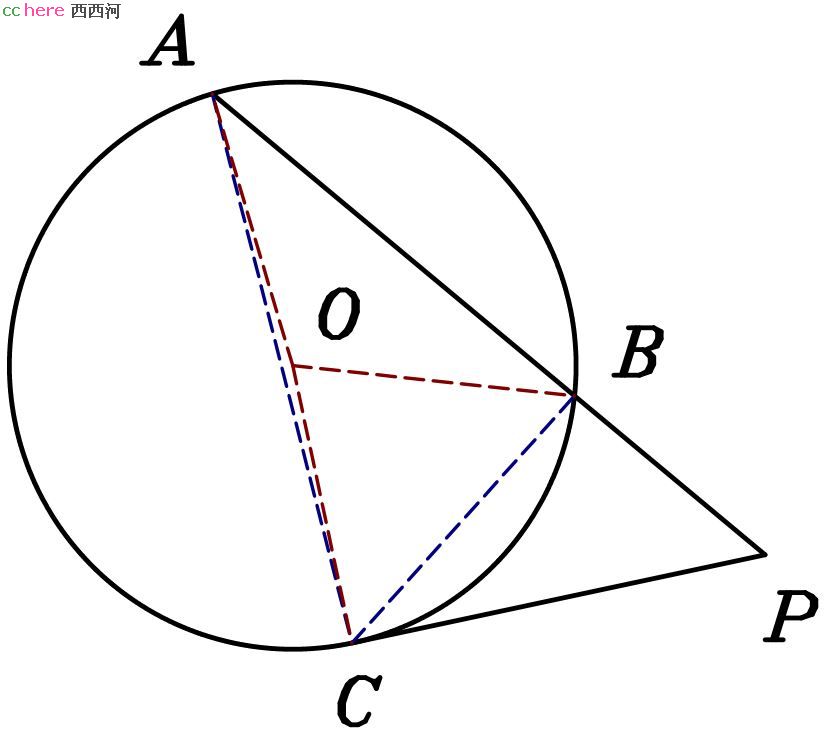
连接OA、OB、OC。PC与圆O相切于C点，故OC与PC垂直，∠PCB+∠OCB = 90°（等式1）。又B、C两点在圆O上，三角形OBC为等腰三角形，故∠BOC+∠OCB+∠OBC = 180°（等式2）且∠OCB = ∠OBC（等式3）。综合式2、3可得∠BOC+2∠OCB = 180°（等式4）。综合式1、4可得∠BOC = 2∠PCB。

同理，三角形OAB及三角形OAC都是等腰三角形，故∠OAC = ∠OCA且∠OAB = ∠OBA。利用三角形ABC的内角和为180°，180° = ∠BAC+∠ABC+∠ACB = ∠BAC+∠OBA+∠OBC+∠OCA+∠OCB = ∠BAC+∠OAB+∠OCB+∠OAC+∠OCB = ∠BAC+（∠OAB+∠OAC）+2∠OCB = 2∠BAC+2∠OCB。这等价于∠BAC+∠OCB = 90°（等式5）。注意到图中O点在三角形ABC的内部，但式5的成立并不需要O点在三角形ABC的内部。综合式4、5可得∠BOC = 2∠BAC。

这样我们得到∠BOC = 2∠PCB且∠BOC = 2∠BAC，故∠PCB = ∠BAC。故三角形PAC与三角形PCB相似。故|PA|/|PC| = |PC|/|PB|，故|PC|2 = |PA|×|PC|。

第二个问题我觉得可以这么理解，要是有个圆与所给直线相切，那么这个圆必然在这个直线的某一侧，它不可能过位于直线异侧的两个点。