- 近期网站停站换新具体说明
- 按以上说明时间,延期一周至网站时间26-27左右。具体实施前两天会在此提前通知具体实施时间
主题:【原创】上帝之书 -- 我爱莫扎特
最后总会拆成有两个“外面”的三角形,中间步骤是凹、凸、平,都无所谓,定义“外面”就是为了把这些情况都包进去。这是一个拆的过程,而过程中C恒定不变。
换言之,凸是一个多余的条件。
嗯,首先多谢各位的指导哈
由于引入点在多面体内部,而且是对每个外平面构造小多面体,所以不存在棱锥重合的问题;
当你说这句话的时候,原图形必须是凸的。举例来说吧,考虑一个非凸四边形:
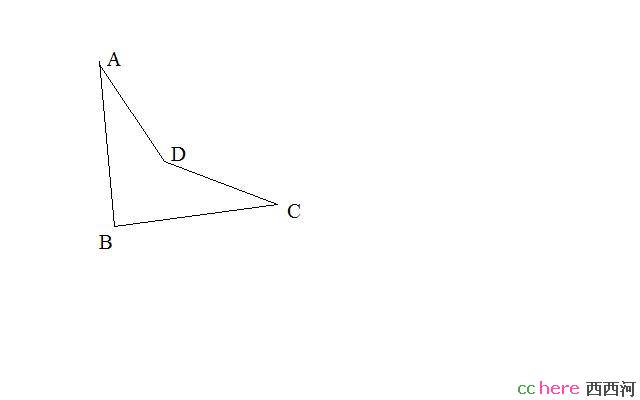
A点与C点的连线跑到了外头。
回头说你的证明,你第一次做“去点”操作时,由于原图形是凸的,当然可以,第二次以后就要打个问号了。
这就是我说的,如果用数学归纳法,必须保证每次点减少后题目条件没有改变。
而且拼接的顺序很有讲究。
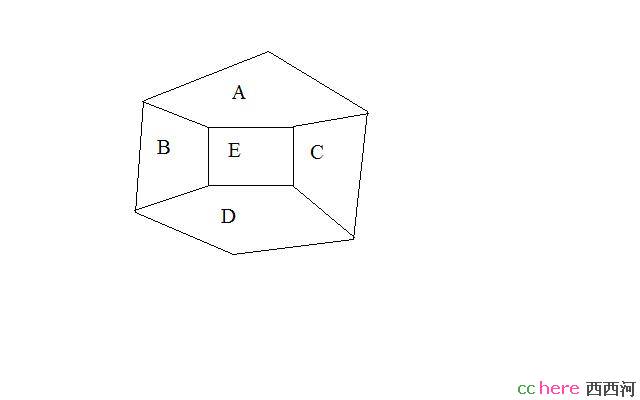
图中,你以ABCDE的顺序拼接和ABCED的顺序区别很大的,你可以算算看。
本帖一共被 1 帖 引用 (帖内工具实现)
的确考虑不周,漏洞百出。
忍住诱惑,就不去翻10年前课本的,就不去Google,。。。
看来不是谁都能成为大师的。
在我的拆法里,外面只有两种:原多面体的面(多边形)和新生成的三角形。你举的例子根本不会出现在我的中间步骤中。
首先感谢几位河友的参与。这道题已经收到周师傅,桑榆非晚,honeybl,Seagul1等河友的解答,此外umggc,bogut等参与了讨论,发表自己的见解及改进意见。
我也参与了大部分讨论。讨论过程中,我表现得比较“严苛”,可能给人吹毛求疵的感觉。我发表的意见纯粹是技术性的,希望没有引起各位的不快。
数学本来就比其他学科严格,而数学的发展过程也是越来越严密化的过程。一些几百年前的证明也许在今天看来算得上漏洞百出,但其中蕴含的思想绝不平凡。从历史上说,欧拉公式虽然是欧拉第一个发现,但他给出的证明按后人的标准看就是不严格的。大约到50多年后才出现真正严格清晰的证明。中间的过程绝非一帆风顺。有兴趣的朋友可以看看珍珠土老鼠提到的《证明与反驳》。
在几位河友的解答中,周师傅和桑榆非晚的思路比较好。
先看周师傅的解答。他的证明的核心思想很清楚,就是对顶点数做数学归纳法。这是正确的思路。事实上我最后公布的一个答案(就是我和肖邦兄说的初中程度能理解的解答)也是这个思路。但周师傅的解法在具体实施时遇到技术上的小困难。
1,加点还是减点。
我们有两种做法。可以一个一个的减少多面体的顶点,并证明过程中等式不变。也可以从一个简单图形(如四面体)出发,一个点一个点往上加,最后重新构造出原来的多面体。注意!两种方法有着很微妙的差别。大家可以考虑一下哪个更好一些。
2,形状的限制。
当我们去除多面体一个顶点后,会发现余下的图形变得比较复杂。此时一种方法是仔细分析新形成的面,但bogut也认为计算会较复杂。另外,umggc提出将新的面划成三角形,这种技术在数学上被称为“三角剖分”,是很有意义的想法。umggc还提出欧拉公式题目中的凸性并不重要,这又是一个很好的观察,说明多面体的形状对证明碍手碍脚,却不改变实质。
桑榆非晚的思路也很好。他相当于是说,我们把多面体的面一块一块“拼接”上去直到最后成为多面体之前,V+F-E=1,而最后一块“塞”进去后,V+F-E=2。我在回帖中提到,“拼接”的顺序会对等式产生影响。见 http://www.ccthere.com/article/2040568 。
小结一下,重要的思路有归纳法(对顶点),和“拼接”(相当于对面做归纳法)。有用的想法有“三角剖分”,以及对多面体形状的适当“忽视”。现在的问题是我们如何把这些好的想法和观察在一个证明里完整清晰的体现出来。
我给大家一点小提示。
事实上欧拉公式不仅对非凸多面体成立,还对其他图形也成立。其中值得一提的有:
1,球面多面体。此时顶点在球面上,棱是球面上的大圆弧。我们仍有V+F-E=2。
2,连通平面图。我们在平面上画一个多边形,并在多边形内部或边上找定一些点,通过这些点和多边形的顶点间相互连线把多边形分割成若干个多边形。另V为点数,F为分割出的小多边形数,E为所有图形的边数。则成立V+F-E=1。
这两种情形和多面体既有联系又有区别。注意到这点会对证明有所帮助。
我这周很忙,无法继续我写的系列。我打算在周六前给出欧拉公式的解答,并在周末继续更新。
我希望有兴趣的朋友继续提供好的证明思路,或者改进已经出现的做法。河友们也可以回帖说说你们对几个证明的看法,以帮助我决定通宝最终的归属。
谢谢大家!
本帖一共被 1 帖 引用 (帖内工具实现)
我觉得这个应该算美且伟大的一个:)
等楼主的解法,把证明讲得严格而浅显是很见功力的。
另外,欧拉的这个公式只牵涉到拓扑一些概念的数量,因此在拓扑不变下,始终是成立的,比如楼主说的两种其他图形。拓扑不变,打个比方来说,就是把边看作橡皮筋,把面看作肥皂膜,可以任意伸缩变动,但原来不相交的还是保持不能相交。
在凸多面体内取一个点,同其他各个点连接起来,则把一个N面凸多面体分解成N个底面分别为凸多面体的各个面的金字塔;或者说,由N个顶点重合的金字塔型组成了N面凸多面体。
于是我们一个一个地拼接。
第一步:第一个金字塔型,假设底面为M边型,则有(M+1)个点,(2*M)条边,(M+1)个面,V-E+F=2。
第二步:拼接一个金字塔,要求其底面必须有一条或以上的边与原来的相邻(这个条件似乎有点多余,不过理解起来方便点)。考虑到顶点重合,假定是K条边相邻,L条边不相邻,则新的图形和原来被拼接的图形相比,增加了(L)个点,(2*L-K)条边,(L-K)个面;所以V-E+F=2仍然成立。
。。。
最后一步:拼接的是一个M边型底面的金字塔,则将减少1个点(顶点没了),M条边(侧边没了),(M-1)个面(侧面没了,但是加一个底面),V-E+F=2仍然成立。
花!