- 近期网站停站换新具体说明
- 按以上说明时间,延期一周至网站时间26-27左右。具体实施前两天会在此提前通知具体实施时间
主题:【原创】兼整理,中庸考辩。 -- 铁手
第一个是对“知之为知之,不知为不知”的辨析,是很有道理的:怎么知道自己真的知道呢?知道到什么程度算知道了呢?自己觉得知道了真的就穷尽了这方面的知识了吗?那如果事物永远知不尽,我们就永远不能说自己的看法了吗?所以说,这种说法还是比较形而上学的,不太符合科学认识论。之前看到一个视频是杨振宁还是丁肇中谈了这个问题,他大概也是这个意思。
第二个是关于对半分这个问题,应该用开区间和闭区间做例子好理解。把一个线段分成两段,中间的点归哪边是要考虑的,所以只能分成一个开区间和一个闭区间,两者不完全一致。
请把我评道家的这三帖也收编进去。
道家的自然(齐物整体)观,故而有“无用之用”,以自由为是,以动态为常,而不偏执于一元还是二元。“彼亦一是非,此亦一是非,果且有彼是乎哉?果且无彼是乎哉?”
https://talkcc.net/article/4990619
庄子的认知:世界(包括人类社会)有其客观性和非目的性, 人类理性是不可靠的,“且夫乘物以游心,托不得已以养中,至矣”。https://talkcc.net/article/4971298
不得已”的阐释:不得已,我的理解是当主观意志与客观条件之间存在矛盾时,要顺应自然,培养中和之心。https://talkcc.net/article/4972107
本帖一共被 1 帖 引用 (帖内工具实现)
想做什么事,往什么方向努力,去做即可。收益多大,成果如何,眼下不可知,事后总结也往往时移世异(过于自我中心主义的抽象概括和理性分析未必是事实真相),不用刻意。儒家认为必然能认知客观规律,我要得其中;道家说,人在自然求道之中,我就中(四声,用河南话读,吴语相近的词可能是惬意或适意)了
也讲得通。黄金分割点。
《庄子·养生主》(庖丁解牛)中有“以无厚入有间”的说法,上学的时候只是当常识理解了。后来发现《墨子》中竟然都是有定义的。
厚,有所大也。
厚。惟无厚无所大。
.
端,体之无厚而最前者也。
端。是无内也。
有间,中也。
有间。谓夹之者也。
.
间,不及旁也。
间。谓夹者也。尺前于区,而后于端,不夹于端与区内。及,非齐及之及也。
《庄子》中说“一尺之棰,日取其半,万世不竭”(其实这是辩家的观点),可以推论出物质是“有间”的,所以才可以分成”半“,而且无论多小都是”有间“。这里说的确实是物质无限可分思想。
无限可分的思想无疑会给人一种无力感,而且也是无法证明的。人类的寿命有限,知道的也有限,”以有涯随无涯,殆矣!“。为了解释各种自然现象,我们可以假设物质不是无限可分,而是会分到一种”最小“的物质,这种物质是不是真的最小其实不是很重要,重要的是这个”最小“物质能解释各种现象,即使不能解释全部,能解释大部分也是有用的啊。这就是所谓的”第一性原理“。古希腊的原子论和中国古代的”气“实际上都是这种思想的产物。
逻辑上,这种”最小“物质一定不是”有间“的。但这里又有两种情况,一种是这个最小物质是有”厚“的,一种是”无厚“的。古希腊的原子论很可能是第一种,但现代原子论更接近后一种:基本粒子如电子等(也包括黑洞奇点)理论上都是没有大小的(弦理论中的”弦“也是有长度但没厚度的)。现代量子论用另一种办法逃避了这个问题,它认为在普朗克尺度下物理学是无法解释的,基本粒子是不是真的没有大小无所谓,反正我假设最小就是普朗克尺度,再小的话问我我也不知道。
所以说,这种说法还是比较形而上学的,不太符合科学认识论。之前看到一个视频是杨振宁还是丁肇中谈了这个问题,他大概也是这个意思。
您说的这个实际上是涉及到“无限”的辨析,《墨子》中对这个有很多论述,理论水平非常高,超越了古希腊(古希腊对无限是比较排斥的,一个无理数就被憋了2000年)。
比如下面这段话,
穷,或有前不容尺也。
穷:或不容尺,有穷;莫不容尺,无穷也。
说不论用有限的长度去量多少次,无限也量不完。这实际上和古希腊阿基米德公理(也叫阿基米德性质)相当。本质上是一样的。
但墨家认为在有限空间内无穷是可“尽”。
无穷不害兼,说在盈否。
无。南者有穷则可尽,无穷则不可尽。有穷无穷未可知,则可尽不可尽未可知。人之盈之否未可知,而必人之可尽、不可尽亦未可知,而必人之不可尽爱也,悖。人若不盈无穷,则人有穷也,尽有穷无难。盈无穷,则无穷尽也,尽无穷无难。
所以说阿基里斯是可以追上乌龟的,因为他只是落后乌龟一段有限的距离,而这段有限距离内即使有无穷多点但是“盈”的,因此“尽无穷无难”。
不知其数而知其尽也。说在问者。
不知其数,恶知爱民之尽之也?或者遗乎?其问也,尽问人,则尽爱其所问。若不知其数而知爱之尽之也,无难。
这里其实已经有了可数性(可列性)的思想,结合上文,可以推出墨家认为可数无穷也是可“尽”的。
这里墨家的反对方很可能是辩家(也称名家),因为从辩家二十一事和历物十事(均记于《庄子》)中有些论题和这里的诘问相似。尤其是这里提到了其中的“南方有穷而无穷”,但貌似在这个问题上双方的观点似乎是一致的。
墨家对“镞矢之疾,而有不行不止之时”的解答尤其精彩:
止,以久也。
止。无久之不止,当牛非马,若矢过楹。有久之不止,当牛马非马,若人过梁。
这里”久“通”宙“,指时间。这段几乎就是现代的”平均速度/率“和”瞬时速度/率“定义。而伽利略当年并没有提出这么明显”瞬时速度/率“定义,而是隐含在对加速度的讨论中。
其实伽利略之前就已经提出过十分类似的看法(一下摘自百度百科”平均速度定理“):
在14、15世纪,人们为这个关键定理提出了大量的算术和几何证明。其中以尼古拉·奥里斯姆的几何证明最为著名。这个证明大约于1350年提出,收在他的《论性质的构形》之中,这本著作对性质的张弛做了最富原创性的也是最完备的处理。
在图中,令线AB代表时间,垂直于AB的线段代表物体Z的速度:从静止点B开始,均匀地增大到最大速度AC。包含在三角形 CBA内的速度强度总量被设想为代表在总时间AB内Z从B出发沿直线BC到C所通过的总距离。令线段DE代表Z在沿AB时间中点测得的瞬时速度。现在,如果Z以DE处的速度匀速运动,在时间AB内从G到F沿线GF运动的总距离由长方形AFGB给出。如果能证明三角形CBA面积等于长方AFGB的面积,就证明了一个从静止开始作匀加速运动的物体所通过的距离等于在同一时间间隔内以匀加速运动时间间隔中点的速度作匀速运动的物体所运行的距离,即Z作匀速运动的距离S=1/2Vf t,等于Z作匀加速运动的距离S=(at^2)/2。
在14、15世纪的欧洲,尤其是意大利,平均速度定理的奥里斯姆的几何证明以及大量的算术证明广为认知。在伽利略《关于两门新科学对话》中,平均速度定律是第三天对话的头一个命题,伽利略的证明与奥里斯姆的极为相似,甚至所用的几何图形都一样,只是伽利略作了一个90°的转向。
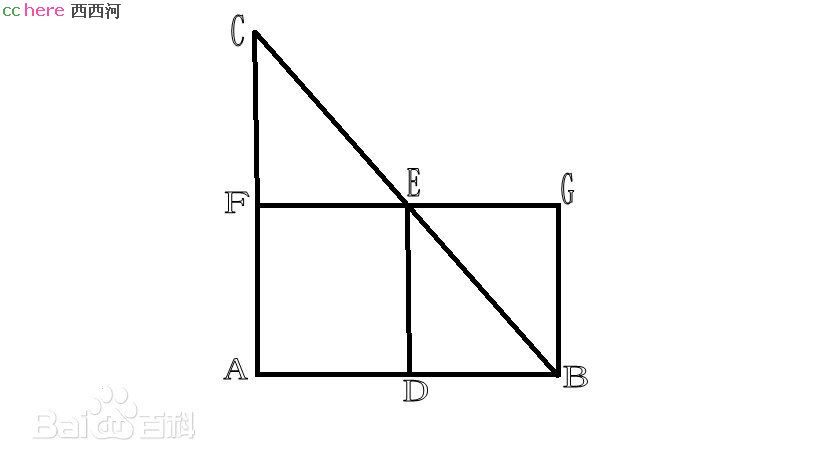
明显看出《墨子》的定义十分直接,但西方确由于古希腊的影响喜欢用几何来说明各种代数和物理问题,十分的绕。到牛顿还是如此,直到实数理论完备才终止。
.
第二个是关于对半分这个问题,应该用开区间和闭区间做例子好理解。把一个线段分成两段,中间的点归哪边是要考虑的,所以只能分成一个开区间和一个闭区间,两者不完全一致。
实际上分法不只一种。”斫必半“说的是不多不少分成完全一样的两半,这是不可能的,如果放松条件的话还是可以分的。
如果不要求不多不少,在两种:
1. 加一个中点,可分成两个一样的闭区间。
2. 去掉中点,可分成两个半开区间。
如果不要求两半完全一样,就是你说的
3. 一个闭区间一个半开区间。
这三种方法其实都是可以的,#1对应的是波尔查诺的二分法,#3对应戴德金分割。现代实数理论基础中有七大定理,其中每一个都可以作为原理推出其余六个,其中闭区间套定理对应波尔查诺的二分法,确界原理对应戴德金分割,聚点原理和有限覆盖原理则用到了#2(有限覆盖原理其实和上面的”有限空间内无穷可尽“的思想是相通的)。
从以上讨论也可以看出西方数学实际上从古希腊到近代是绕了一个非常大的圈子,而中国的数学方向反而是一条直线直通近现代。
#2中如果去掉的不是一个点而是一个中电对称的线段(开的),那么对两边分别继续“日取其半”就得到康托三分集。
取一条长度为1的直线段,将它三等分,去掉中间一段,留剩下两段,再将剩下的两段再分别三等分,各去掉中间一段,剩下更短的四段,……,将这样的操作一直继续下去,直至无穷,由于在不断分割舍弃过程中,所形成的线段数目越来越多,长度越来越小,在极限的情况下,得到一个离散的点集,称为康托尔三分集,记为P。
在追求最优化的目标的过程中,有一点是不可忘记的:
同感。
这就是“世事古难圆”,大白话就是“天下不会掉馅饼,舍不得孩子套不了狼”,“水清无鱼”……。
”得”的前提是“失”,“取”的代价是“舍”……。每个人,每件事,万物在发展和优化的过程里,就是在不断的得失的舍取中,平衡着和挣扎着……。
推荐一部电视剧“山花烂漫时”,它比较真实地表现了“办成事”的过程。
看到许多河友的争论,当各执一词时,好像都离开了我们现在真正面对的那个世界。
一家之言。
执两用中
“执其两端,用其中于民,其斯以为舜乎?”
五音律,12平均律相通哇
歪个楼,请大家多包涵,多指教。
“记得小苹初见,两重心字罗衣”,“银字笙调,心字香烧”。这里里银字,心字,是指图案吗?
“吾有知乎哉,无知也,有鄙夫问于我,空空如也,我叩其两端而竭焉”。
当然墨子的问题本身就是对孔子观点的“叩其两端”,具体回答,还要从孔子“叩其两端”这番话继续“叩其两端”,这里就不展开了。
传统上,这叫“究天人之际”。这个思想应该远比孔子古老。
古希腊人也有类似的思考。
芝诺的学生曾经问他:“您的知识比我的知识多许多倍,您对问题的回答又十分正确,可是您为什么总是对自己的解答有疑问呢?”芝诺顺手在桌上画了一大一小两个圆圈,并指着这两个圆圈说:“大圆圈的面积是我的知识,小圆圈的面积是你们的知识。我的知识比你们多。这两个圆圈的外面就是你们和我无知的部分。大圆圈的周长比小圆圈长,因此,我接触的无知的范围也比你们多。这就是我为什么常常怀疑自己的原因。”
芝诺的“圆圈”,也就是“天人之际”。
在这一点上,中国古贤者与希腊哲学家其实是相通的。
在一个讲中庸的帖子里讲追求极致,跑题了。不过,中国人在某些方面确实是极其追求极致的,夸父追日、精卫填海、愚公移山。几乎所有在人类历史长河中辉煌闪耀过的文明都在某一方面有着极致追求,在这一点上,古希腊并不孤独,“对终极的追求”也并不为其专美。
“三分损益法”既可以生成“五声音阶“,也可以生成”十二律“。但这个十二律只是”十二平均律“的近似。因为”十二平均律“是2的12次方根,是个无理数,但”十二律“是按3的n次方分之一生成的,是个分数也就是有理数,两者不可能完全相等。但后者也正因为是个分数所以实践中更容易做出来,所以”十二平均律“提出后很长一段时间并没有得到重视。(实际上何承天在公元400年左右就已经得到了1.060070671这个数字,和一千多年后朱载堉得出的已经十分接近,对实际应用精度也差不多够了,但实际上却仍然几乎没有乐器按”十二平均律“,所以很可能还是客观条件限制了这方面的发展)。
而且”十二律“和”十二平均律“背后的基础实际上也是不一样的,前者是基于”音的频率变为3/2倍(也即1.5倍)后,呈现非常和谐的音程关系。“,后者是基于”音的频率变为2倍后,两个音呈现完美和谐的音程关系。“。这里的”非常和谐“和”完美和谐“主要是基于人的感受(可能和生理构造),两者如此接近只能说是个巧合。
”十二律“的缺陷是不能实现完美转调,但”十二平均律“能,所以后来在钢琴等乐器中用了后者(其实也有了200多年),使音乐作品的创作自由度和演奏效果大大提高。
朱载堉可能是个完美主义者,他竟然计算了24位小数(1.059463094359295264561825),好在他本人就是个算学家才能完成这么个工作,据说他特制了一个双排81档的算盘,计算了两次平方根一次立方根,得到”十二平均律“数表,并且没有差错。几十年后梅森(就是提出梅森素数那个)在1630年得出了另一个表,但是只有9位小数。同一年数学家Johann Faulhaber得出了另一个表,比梅森的更加精确。
君子无所不用其极,来自大学-礼记
汤之盘铭曰:「茍日新,日日新,又日新。」《康诰》曰:「作新民。」《诗》曰:「周虽旧邦,其命惟新。」是故君子无所不用其极。
从这篇内容,重点是“修身养性齐家治国平天下”
物格而后知至,知至而后意诚,意诚而后心正,心正而后身修,身修而后家齐,家齐而后国治,国治而后天下平。
无所不有其极的极我觉得应该是极致的意思。
趁着这个机会去重读了一下原文,读懂了一些,也还是读不懂一些😄。
确实,我以前也没注意到这个庸字的意思。
现在想想,也确实有很多带庸的词语都表示“平常”的意思。