主题：阿波罗尼奥斯问题-Prob. of Apollonius -- 理性网民

令给定点A、B的坐标分别为(xA, yA)、(xB, yB)，给定圆圆心C的坐标为(xC, yC)，半径为rC。假设所求圆圆心为(x, y)，半径为r。那么PPC问题等价于求解如下非线性方程组。其中xA、yA、xB、yB、xC、yC、rC为已知量，x、y、r为未知量。

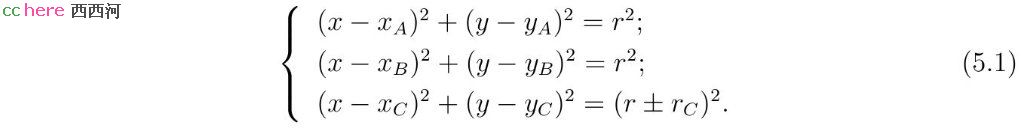
方程组（5.1）的第一式要求点A在所求圆上。第二式要求点B在所求圆上。第三式要求圆C与所求圆相切。由于两个圆可以外切也可以内切，第三式右侧可以取正号也可以取负号。

为了求解方程组（5.1），用第一式减去第二式。考虑到第三式的正负号问题，令r可以取正值也可以取负值。这样可以得到如下等价方程组

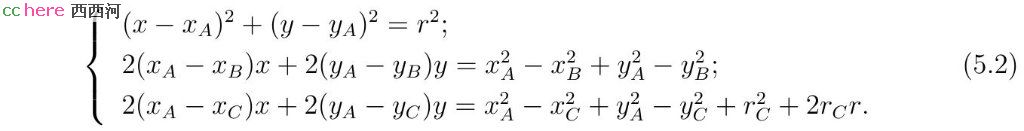
方程组（5.2）的第二式要求所求圆圆心在线段AB的中垂线上。第三式要求所求圆圆心位于与线段AC垂直的某条直线上。

方程组（5.2）的后两式可将x和y表示成为r的函数。将r当作已知，行列式det(A)可以用于判断方程是否有解。

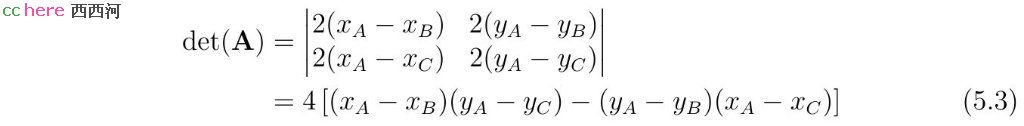
当det(A)为零时，A、B、C三点共线。为使方程组有解，方程组后两式的系数必须成比例。相应的r值为

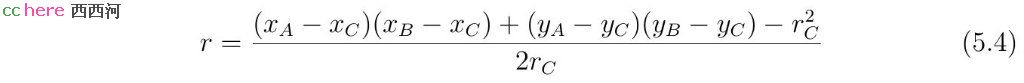
得到r值以后，x和y值可以根据方程组（5.2）的后两式求出。

当det(A)不为零时，令

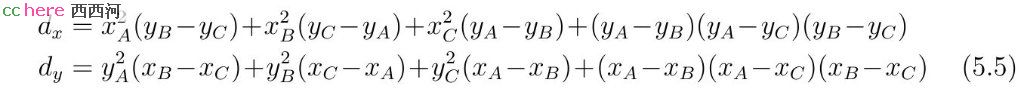
x和y可以表示成为r的函数。

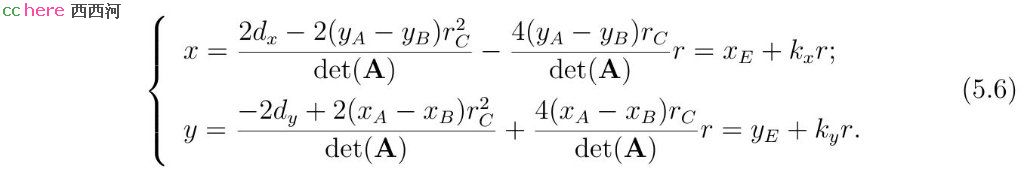
其中E点(xE, yE)在线段AB的中垂线上，(kx, ky)为与线段AB垂直的向量。向量(kx, ky)的长度为

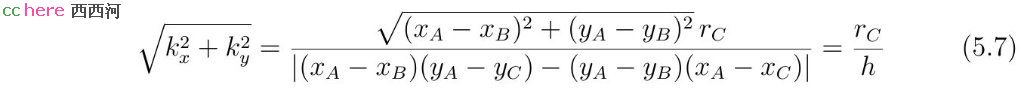
其中h为圆心C到AB所在直线的距离。将式（5.6）代入方程组（5.2）的第一式，可以得到r需要满足的方程，其可以变换成如下一元二次方程形式。

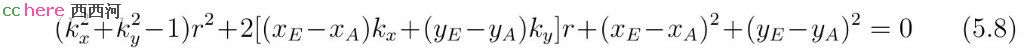
当h = rC时，AB所在直线与圆C相切，式（2.9）二次项系数为零，r有一个实数解。当h ≠ rC时，式（5.8）判别式为

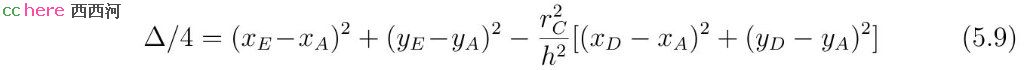
r的解的个数取决于Δ/4的大小。将式（5.6）xE、yE的表达式代入式（5.9）中，可以看出Δ/4为关于rC2的二次函数。该二次函数二次项（关于rC2的二次项，即rC4）系数为正，当rC2 = 0时取值为正。可以证明，当rC等于|AC|或者|BC|时，Δ/4 = 0。因此，当点A、B位于圆C同侧时，Δ > 0，r有两个相异的实数解；当点A、B中某点位于圆C上时，Δ = 0，r有一个实数解；当点A、B位于圆C异侧时，Δ < 0，r无实数解。得到r值以后，x和y值可以根据方程组（5.6）求出。