- 近期网站停站换新具体说明
- 按以上说明时间,延期一周至网站时间26-27左右。具体实施前两天会在此提前通知具体实施时间
主题:阿波罗尼奥斯问题-Prob. of Apollonius -- 理性网民
问题:给定两点A、B及圆C,找出过A、B两点且与圆C相切的圆(如图)。
解:过A、B两点做圆D与圆C交于P、Q两点。过A、B两点做直线a。过P、Q两点做直线b。两直线a、b相交于O点。在圆C上找到点S满足|OS|^2 = |OA|×|OB|。过A、B、S三点做圆,则其与圆C相切于S点。
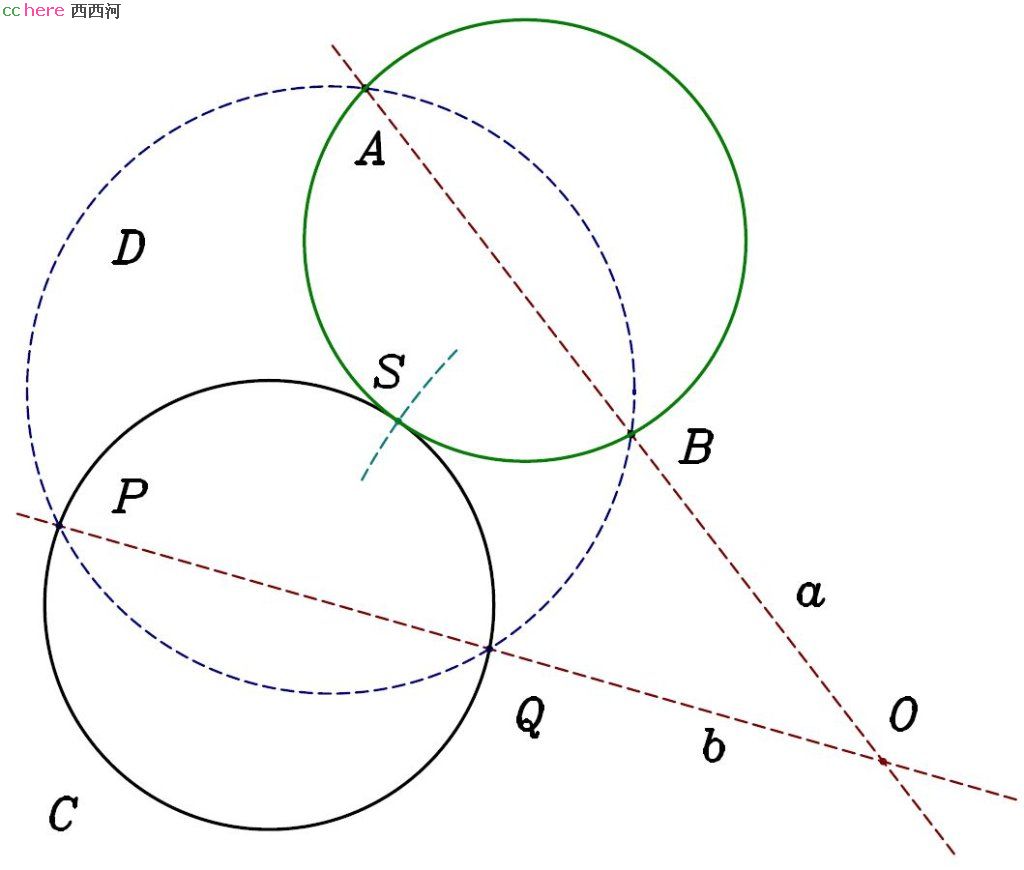
证明:连接OS。因为|OS|2 = |OA|×|OB|,所求圆与OS相切于S点。因为A、B、P、Q四点共圆,|OA|×|OB| = |OP|×|OQ|。那么|OS|2 = |OP|×|OQ|,故圆C同样与OS相切于S点。故所求圆与圆C相切与S点。
分析:当a与b相交于O点,在圆C上有两点与O点距离满足等式|OS|2 = |OA|×|OB|。这两点对应于问题的两个解。当a与b平行时,圆C的圆心与切点S都在线段AB的中垂线上。此时问题同样有两个解。当A、B中有一点位于圆C上时,过此点及圆C圆心做直线。如AB不与圆C相切,则所求圆圆心位于该直线与AB中垂线交点上。此时问题只有一个解。当A、B中有一点位于圆C上时且AB与圆C相切,或者A、B两点位于圆C异侧时,PPL问题无解。当A、B两点位于圆C上,唯一满足条件的圆为圆C本身。解的数目总结如下。
- 两个解:A、B两点同时位于圆C内侧或者外侧;
- 一个解:A、B两点中有一点位于圆C上且AB不与圆C相切;
- 无解:A、B两点中有一点位于圆C上且AB与圆C相切,或者A、B两点位于圆C异侧,或者A、B两点位于圆C上。
评论:点O的位置并不依赖于圆D的选择。从证明可以看出,O的位置实际由圆C及所求圆的公切线所决定。与PPL问题类似,如果采用点O作为反演中心,且选取|OS|2为变换常数,那么在变换前后,A、B两点位置互换,圆C与圆D都保持不变。由于圆D选取的任意性,可以看出,任何过A、B两点的圆都在变换前后保持不变。
- 相关回复 上下关系8
🙂【6】PCC问题 1 理性网民 字3141 2020-07-31 15:07:07
🙂【6.1】解析几何方法 理性网民 字2920 2021-02-07 13:13:58
🙂【补充】基于向量的公式推导 1 理性网民 字1702 2021-02-07 13:18:58
🙂【5】PPC问题

🙂【5.2】解的存在性和个数 1 理性网民 字960 2020-11-09 10:05:39
🙂【5.1】解析几何方法 1 理性网民 字2718 2020-10-16 12:06:53
🙂【补充】E点的几何意义 1 理性网民 字760 2020-10-16 12:09:49
🙂【4】LLC问题 3 理性网民 字2373 2020-07-26 23:49:20