主题:【原创】上帝之书 -- 我爱莫扎特
好帖,花一个
PS。窃以为欧拉公式的这种形式更具美感
exp(i*theta)=cos(theta)+i*sin(theta)
也很有用,除了它是复变函数基础外,还可以用来推导三角函数公式。俺考试的时候从来不记三角公式的和差化积积化和差之类,都是直接从欧拉公式开始推倒,最多一分钟搞定。
我贴的那种形式最有趣的地方在于,它把科学中用到的最重要的数都包括在内了:
0,1,i,e,Pi
其实麦克斯韦八大方程是指他在1865的论文中所提出的八个方程(麦克斯韦自己写了20个,因为他把三维情况的每个方向都单独写了,囧囧囧囧囧),基本上就是总结前人定律的:
Ampere定律、Ohm定律、高斯定理这三个
加上电场力和磁场力的两个
再加上介电常数定义以及引入位移电流(这个是他的发明)的总电流方程两个
还有一个电荷的连续性方程
总共八个
很繁琐,后来一个英国自学成材的牛人Oliver Heaviside出手,把它简化成了四个矢量(这个很厉害)方程,基本上就是
静电场散度正比于静电荷,磁场散度恒零(也可以记成静电场有源,磁场有旋无源),磁生电,电生磁四个,任何一本电动力学教科书上都能找到,俺就不写出来了。
所以物理学界也有人一直坚持说应该叫化简后的四个方程为Heaviside方程组
所以是有人还叫“八大方程”,我上学时有老师这么说。
楼主加油,我觉得写得很好,继续,我会一直关注送花
书里面有一个公式就会跑掉一半的读者,这篇文章出现了四个公式,只剩下十六分之一的读者了。
希望挽回一些影响。
后面公式越来越多,有些地方会比较难,我尽量通俗的讲。同志们挣扎着看吧。
有意见要告诉我啊,比如太难啦,太浅啦,太罗嗦啦?
哪位大拿有兴趣讲讲这些方程的?还有背后的故事。我很想听听的。
这些简单而优美的方程总是那么令人心动啊~~~
为啥?想了半天也没想明白,汗。。。
“直线”在这里指的是大圆。球面上任意两个大圆都相交,且交于对径的两点。
椭圆几何要对球面几何再做点小手术,这样产生的“直线”就总相交于一个点了。
呵呵,写得有点累,(中)这部分大概还有3段,然后(下)还有2段的样子。基本构思好了,不过自己的工作也忙,所以只好慢慢写。
大家很捧场,作为新人来说我很欣慰。不过还是觉得发言的童鞋不够多啊。大家有什么意见尽管提,我也好提高提高嘛。
想活跃一下气氛,给大家出个题。真诚的希望大家热情参与。
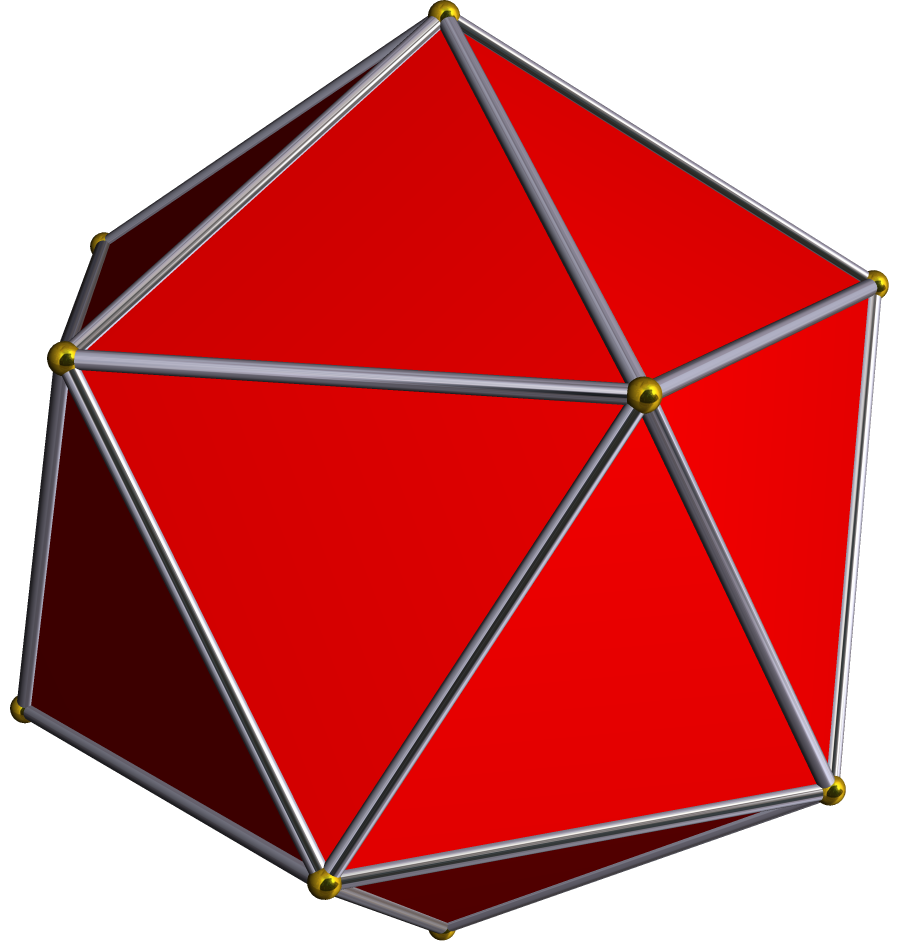
欧拉公式:
给定一个凸多面体,记它的定点数,棱数,面数分别为V,E,F,试证明:V-E+F=2
这个公式很美很深刻,属于我说的“简单而不平凡”的例子。且和我后文有一点点关系。
而且它的证明不太复杂,我可以保证用几句话就能讲清楚,且让学过初中数学的朋友都能明白。
希望大家独立思考,给出你们的解法。也可以回帖说自己的思路。只要是有意义的讨论,我一律送花伺候。
第一个给出正确答案的朋友我会赠送通宝一枚。(肉痛啊,自己的通宝就那么几个)不过要求他的解答明白易懂,比方说要有3个以上的网友回复说“我看懂了”,呵呵。
还有数学专业的同志,wiki或google专业的同志建议忍一忍,咱们要鼓励多参与,多独立思考,对不?当然你们可以写点欧拉公式背后的故事,我一律送花支持。
我过几天公布我的解法,要是着急的话,可以送花催我,哈哈。
本帖一共被 2 帖 引用 (帖内工具实现)
鲜花已经成功送出。
此次送花为【有效送花赞扬,涨乐善、声望】