- 近期网站停站换新具体说明
- 按以上说明时间,延期一周至网站时间26-27左右。具体实施前两天会在此提前通知具体实施时间
主题:阿波罗尼奥斯问题-Prob. of Apollonius -- 理性网民
问题:给定点A、直线l、圆C,找出过点A并与直线l、圆C相切的圆(如图)。
解:过圆C圆心做直线与l垂直,并与圆C相交于O、P两点,与直线l相交于Q点。过A、P、Q三点做圆D,与O、A两点连线相交于R点。那么所求圆必通过R点,可以采用PPL问题的解法(或者PPC问题的解法)。
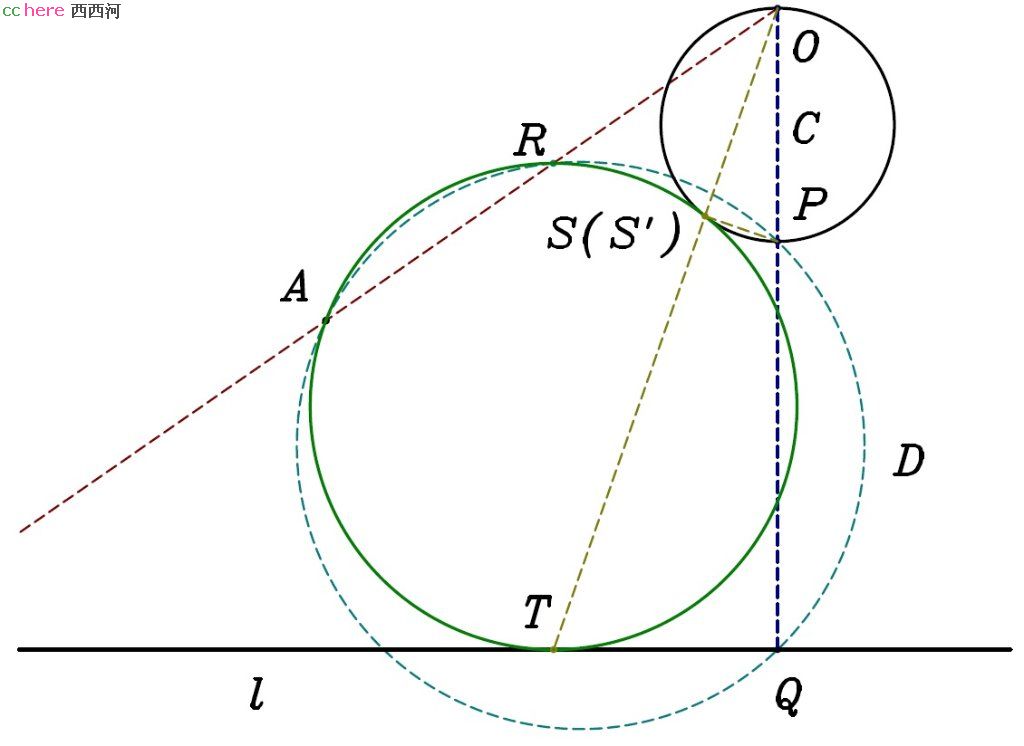
证明:采用PPL解法,假设所作圆与直线l相切于T点。连接O、T两点,与所作圆相交于S点,与圆C相交于S′点。A、R、S、T四点共圆,故|OA|×|OR| = |OS|×|OT|(等式1)。A、R、P、Q四点共圆,故|OA|×|OR| = |OP|×|OQ|(等式2)。连接P、S′两点,则S′在以OP为直径的圆C上,故∠OS′P = 90°。又OQ所在直线与l垂直,故∠OQT = 90°。综合以上可得三角形OPS′与三角形OTQ相似,故|OP|/|OS′| = |OT|/|OQ|,或者说|OP|×|OQ| = |OS′|×|OT|(等式3)。综合等式1、2、3可得|OS|×|OT| = |OS′|×|OT|。故|OS| = |OS′|,也就是说S与S′重合。这样我们证明了所求圆与圆C有一个交点。假设所求圆与圆C有另一个交点S″,那么连接OS″,可以采用类似的方法证明OS″所在直线经过l与所求圆的交点。这与l与所求圆相切矛盾。故所求圆与圆C相切与S点。
分析:在上面的分析中,O点可以位于远离l的一侧,相应的PPL问题最多有两个解。类似的,O点可以位于靠近l的一侧,相应最多可以得到另两个解。这样PLC问题最多有四个解。
评论:如果以O点为反演中心,|OS|×|OT|为变换常数,那么在变换前后圆C与直线l互换,所求圆保持不变。如果我们把直线l看成半径无限大的圆,PLC问题与PCC问题一模一样。
在上面这个图中,因为 PC是圆切线,并且 ∠BCP 和 ∠CAP 对应同一段弧,所以这两个角度值相同。
加上共同的夹角 ∠BPC,∠CPA。
所以 三角形 ACP 和 CBP 两者相似。
因此三角形的对应边成比例,于是 CP/AP = BP/CP,
也就是说 CP^2 = AP * BP
对应到你前面那个图,就是 OP^2 = OA * OB。
我在慢慢一步一步看你的解。以前学的东西,也慢慢回来一些。动动脑筋,感觉很好。
我的证明里面第二段第三段赤膊上阵,证明了弦切角等于圆周角等于圆心角的一半,所以繁琐一些。
这也是写这个帖子的目的吧。一方面想把这个问题的方方面面都写出来,运动运动脑子,另一方面就是想锻炼锻炼写作,毕竟自己懂和写出来让大家懂区别大了去了。
问题:给定圆A、圆B和直线l,找出与圆A、圆B、直线l同时相切的圆(如图)。
解:不失普遍性,假设圆A半径小于圆B半径。过B圆圆心做同心圆B′,其半径与圆B差值为圆A半径。将直线l平移得到直线m,平移的距离等于圆A半径。过点A做圆D与圆B′、直线m相切(PLC问题)。过D圆圆心做同心圆,其半径与圆D差值为圆A半径,即为所求。
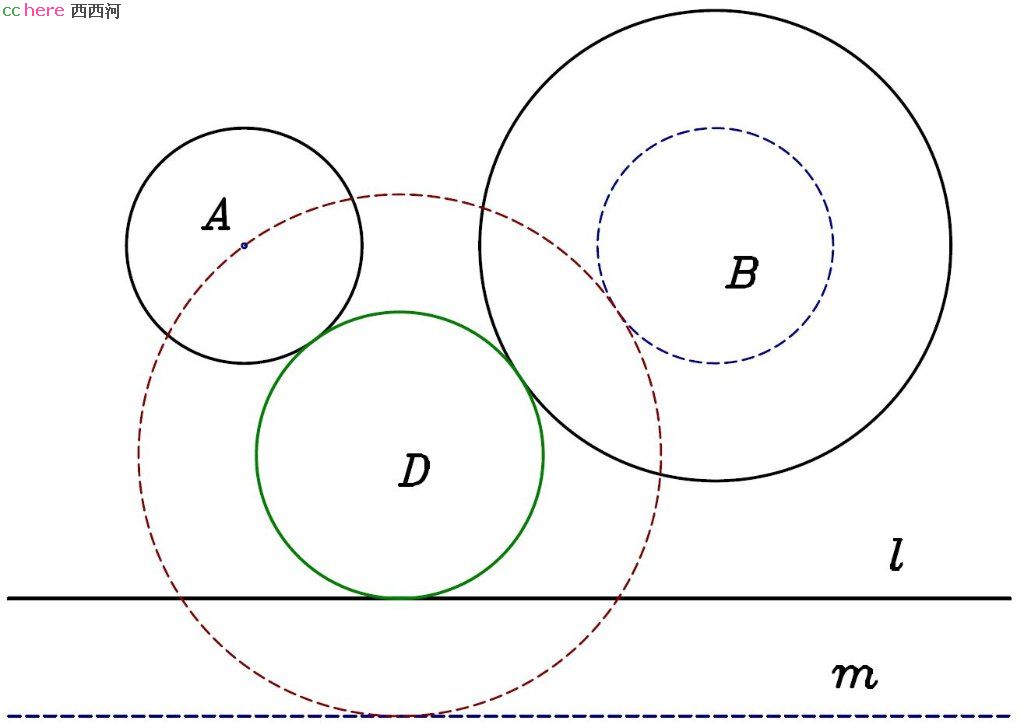
证明:由于两圆相切时,切点一定位于两圆圆心连线上;圆与直线相切时,切点与圆心的连线与直线垂直。故当圆A、圆B的半径同时增加或减少相同的长度,且将直线l平移相同的长度,与它们同时相切的圆的圆心位置不变。这样,我们可以令圆A的半径减小到零,退化为一个点,将LCC问题转化为PLC问题求解。
分析:在上面的求解中,圆B可以增大或者减小,且直线l可以有两个平移的方向,故一共有四种组合。每一种组合对应于一个PLC问题。由于每一种组合实际限制了所求圆与给定圆的相切方式(内切或者外切),相对应的PLC问题最多只有两个可行解。这样LCC问题最多有八个解。
评论:PLC和LCC问题(以及PPP问题、PPL问题或者PPC问题)组成了阿波罗尼奥斯问题的第三个系列。在这个系列中,同样可以看到反演中心和圆的缩放是求解的中心技巧。特别需要指出,PLC问题与PCC问题之间,LCC问题与CCC问题之间,无论是解法还是证明,都有着严格的对应关系。这是因为我们可以把PLC问题和LCC问题中出现的直线看成半径无限大的圆。
问题:给定直线l、m、n,找出与l、m、n同时相切的圆(如图)。
解:过直线l、n交点A做角平分线a。过直线l、m交点B做角平分线b。直线a、b相交于O点。过O点做直线c垂直于n,且垂足为P点。以O点为圆心,|OP|为半径做圆,即为所求。
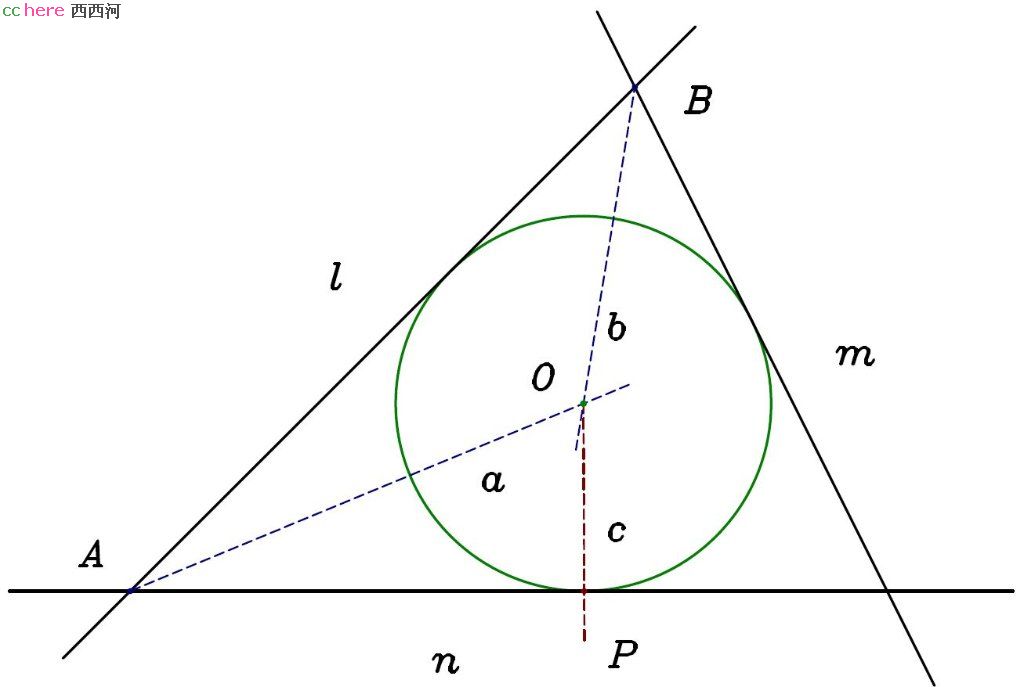
证明:角平分线上的点到两直线的距离相等,故O点到l的距离等于O点到n的距离,且O点到m的距离等于O点到l的距离,且都为|OP|。故以O点为圆心、|OP|为半径的圆与l、m、n同时相切。
分析:在上面的求解中,当三条直线两两相交时,过A点和B点可以分别做两条角平分线,它们的交点都可以做所求圆的圆心,此时LLL问题有四个解。当三条直线中两条直线平行时,LLL问题有两个解。当三条直线相交于同一点时,或者三条直线互相平行时,LLL问题没有解。
评论:LLL问题是阿波罗尼奥斯问题中特殊的一个。通常的解法并不需要将其转化为PPP问题求解。不过下面可以提供另一种思路,将其转化成PPP问题求解。令l与n交点为A、l与m交点为B、m与n交点为C。以A点为圆心、(|AB|+|AC|−|BC|)/2为半径做圆与l、n分别相交于P、Q两点。类似地,以B点为圆心、(|AB|+|BC|−|AC|)/2为半径做圆与m交于R点。过P、Q、R三点做圆(PPP问题),即为所求。可以证明,P、Q、R三点即为所求圆与l、m、n的切点,且|AP| = |AQ|,|BP| = |BR|,|CQ| = |CR|。
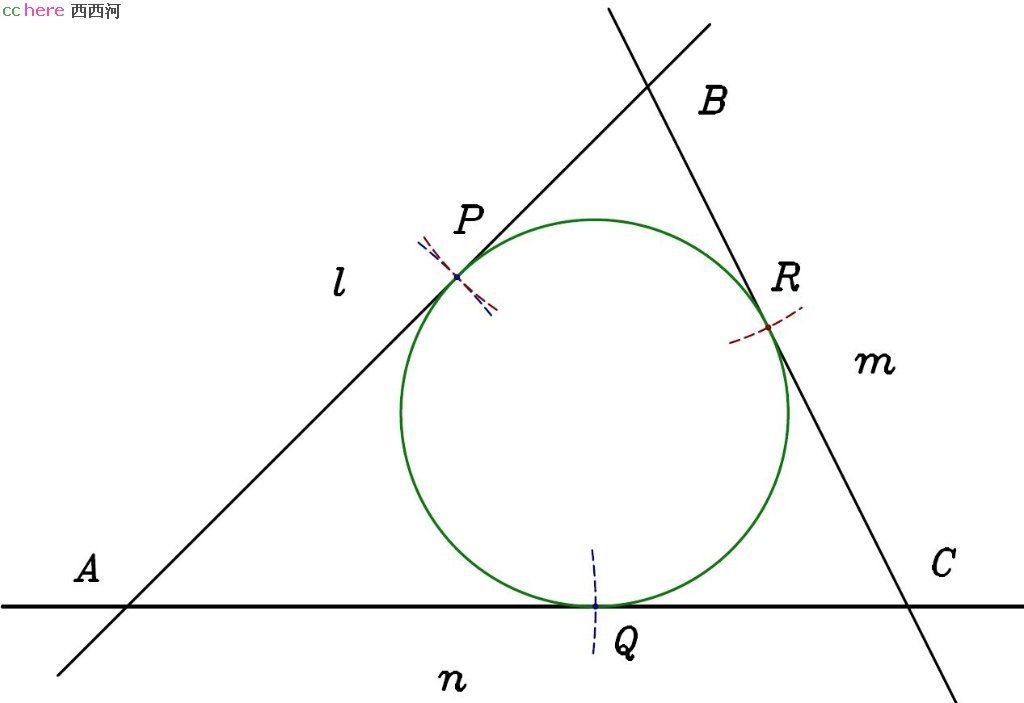
这个方法实现更简单
所求圆的圆心到直线l的距离等于到点A的距离,比到AB所在直线的距离稍大。
PPP问题可以用解析几何的语言进行描述及求解。令给定点A、B、C的坐标分别为(xA, yA)、(xB, yB)、(xC, yC)。假设所求圆圆心为(x, y),半径为r。那么PPP问题等价于求解如下非线性方程组。其中xA、yA、xB、yB、xC、yC为已知量,x、y、r为未知量。
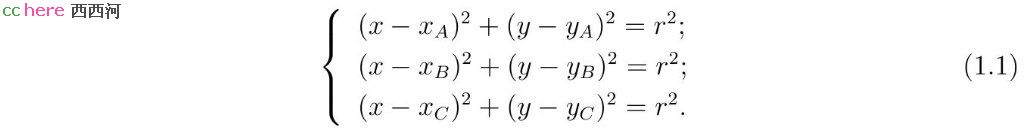
方程组(1.1)的第一式要求点A在所求圆上。第二式要求点B在所求圆上。第三式要求点C在所求圆上。
为了求解方程组(1.1),用第一式减去第二式,并用第一式减去第三式。这样可以得到如下等价方程组
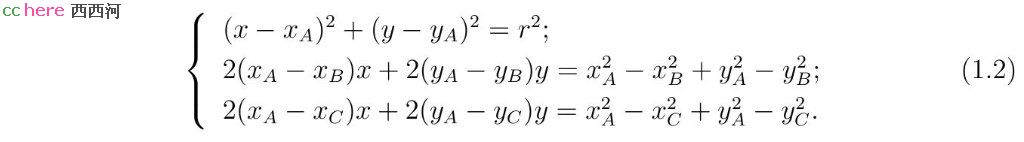
方程组(1.2)的第一式要求点A在所求圆上。第二式要求所求圆圆心在线段AB的中垂线上。第三式要求所求圆圆心在线段AC的中垂线上。
方程组(1.2)的后两式组成一个关于x和y的二元二次方程组。它们可以解释为求线段AB和线段AC中垂线的交点。此二元二次方程组的行列式det(A)可以用于判断方程是否有解。
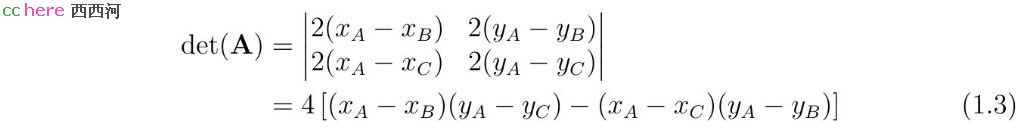
当det(A)不为零时,x和y的解存在。将其代入第一式可以得到r的值。此时A、B、C三点不共线。当det(A)为零时,x和y的解不存在。此时A、B、C三点共线。
两条直线a、b最多有一个交点,所以PPP问题最多有一个解。当a、b没有交点时,意味着a、b平行,那么A、B、C三点共线。这种情况下PPP问题无解。
解的数目总结如下。
- 当A、B、C共线:无解;
- 当A、B、C不共线:一个解。
令给定点A、B的坐标分别为(xA, yA)、(xB, yB),给定直线l经过点(xC, yC)且其法线与x轴正向夹角为θ。假设所求圆圆心为(x, y),半径为r。那么PPL问题等价于求解如下非线性方程组。其中xA、yA、xB、yB、xC、yC、θ为已知量,x、y、r为未知量。
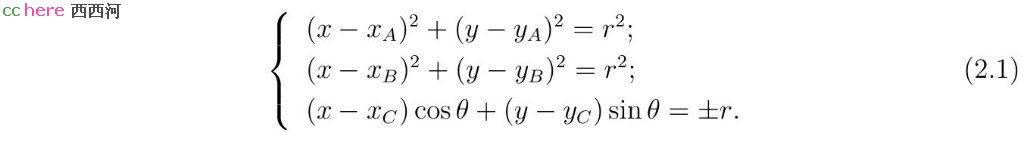
方程组(2.1)的第一式要求点A在所求圆上。第二式要求点B在所求圆上。第三式要求直线l与所求圆相切。由于一个点到一条直线的距离可以是正值也可以是负值,第三式右侧可以取正号也可以取负号。
为了求解方程组(2.1),用第一式减去第二式。考虑到第三式的正负号问题,令r可以取正值也可以取负值。这样可以得到如下等价方程组
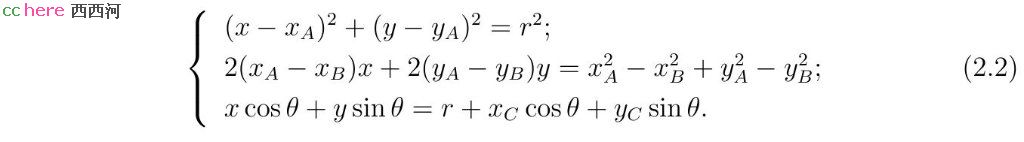
方程组(1.2)的第二式要求所求圆圆心在线段AB的中垂线上。
方程组(1.2)的后两式可将x和y表示成为r的函数。将r当作已知,行列式det(A)可以用于判断方程是否有解。
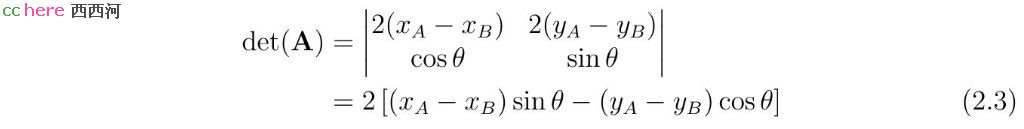
当det(A)为零时,线段AB与直线l垂直,而线段AB的中垂线与直线l平行。为使方程组有解,方程组后两式的系数必须成比例。相应的r值为
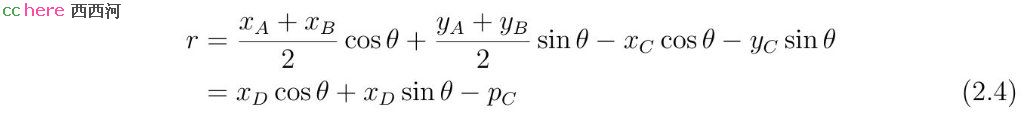
其中D点(xD, yD)为A、B两点的中点,pC为坐标原点到直线l的距离。得到r值以后,x和y值可以根据方程组(2.2)的前两式求出。
当det(A)不为零时,令
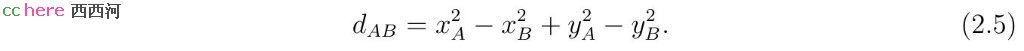
x和y可以表示成为r的函数。
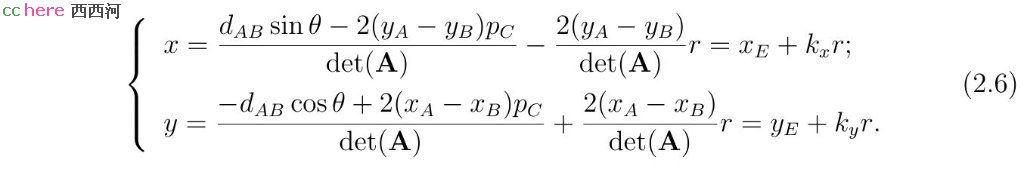
其中E点(xE, yE)为线段AB的中垂线与直线l的交点,(kx, ky)为与线段AB垂直的向量。向量(kx, ky)的长度为
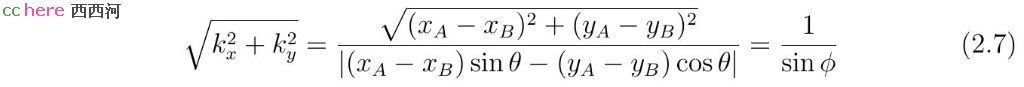
其中ϕ为线段AB的中垂线与直线l的夹角。将式(2.6)代入方程组(2.2)的第一式,可以得到r需要满足的方程。
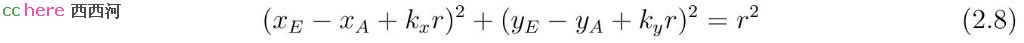
式(2.8)可以变换成如下一元二次方程形式。
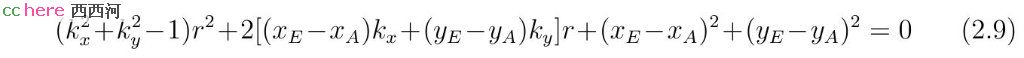
当sin(ϕ) = 1时,线段AB与直线l平行,式(2.9)二次项系数为零,r有一个实数解。当sin(ϕ) < 1时,式(2.9)判别式为
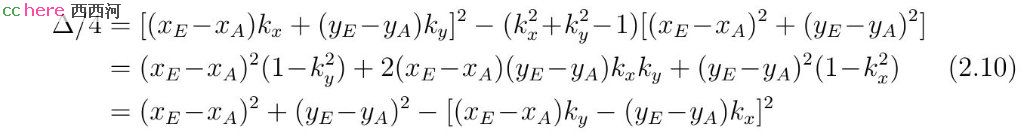
根据向量(kx, ky)的几何意义,可以将式(2.10)的最后一项变换为
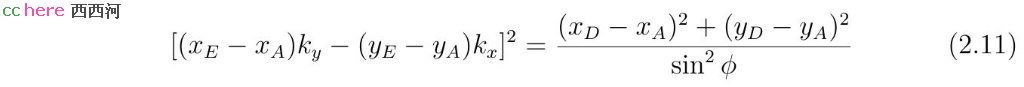
将式(2.11)代入,式(2.10)等价于
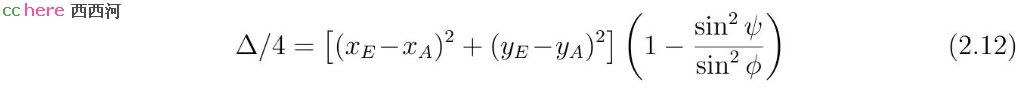
其中ψ为线段AE和线段DE之间的夹角AED。当ψ > ϕ,点A、B位于直线l异侧,此时Δ < 0,r无实数解。当ψ = ϕ,点A、B中某点位于直线l上,此时Δ = 0,r有一个实数解。当ψ < ϕ,点A、B位于直线同侧,此时Δ > 0,r有两个相异的实数解。得到r值以后,x和y值可以根据方程组(2.6)求出。
当线段AB所在直线与直线l平行时,切点P在线段AB的中垂线上。此时问题只有一个解。当线段AB所在直线与直线l相交时,根据A、B两点与直线l的相对位置,PPL问题可以有两个解,一个解,或者无解。
解的数目总结如下。
- 当AB与直线l平行:一个解;
- 当AB与直线l相交:a. A、B两点位于直线l同侧:两个解;b. A、B两点中有一点位于直线l上:一个解;c. A、B两点位于直线l异侧,或者A、B同时在直线l上:无解。
令给定点A的坐标为(xA, yA),给定直线l、m分别经过点(xB, yB)、(xC, yC)且其法线与x轴正向夹角分别为θl、θm。假设所求圆圆心为(x, y),半径为r。那么PLL问题等价于求解如下非线性方程组。其中xA、yA、xB、yB、xC、yC、θl、θm为已知量,x、y、r为未知量。
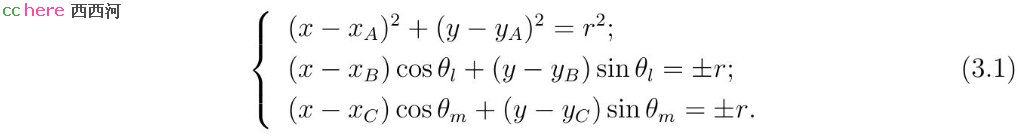
方程组(3.1)的第一式要求点A在所求圆上。第二式要求直线l与所求圆相切。第三式要求直线m与所求圆相切。同样,由于一个点到一条直线的距离可以是正值也可以是负值,第二式和第三式的右侧可以取正号也可以取负号。
方程组(3.1)的后两式可以看作关于x和y的二元二次方程组。令r可以取正值也可以取负值。方程组(3.1)的后两式等价于如下方程组。
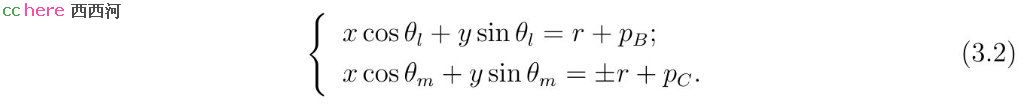
其中的正负号代表两式对应的r值符号不同。pB、pC分别为坐标原点到直线l、m的法线长度。
将r当作已知,行列式det(A)可以用于判断方程是否有解。
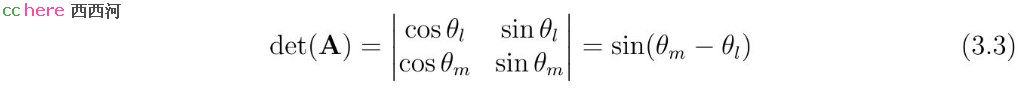
当det(A)为零时,直线l、m互相平行,θm = θl或者θm= θl + π。由于l、m不重合,为使方程组有解,相应的r值为
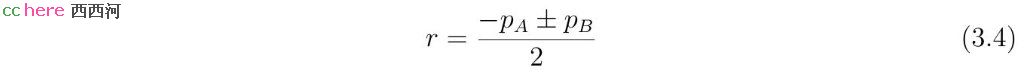
得到r值以后,x和y值可以根据方程组(3.1)的前两式求出。
当det(A)不为零时,x和y可以表示成为r的函数。
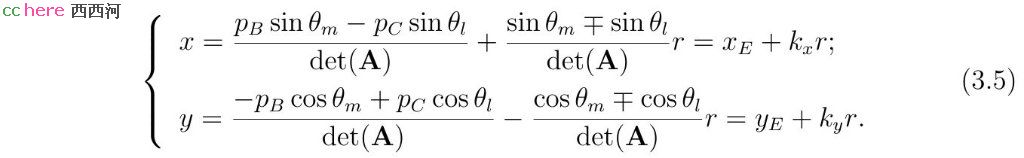
其中E点(xE, yE)为直线l与直线m的交点,(kx, ky)为与角平分线a平行的向量。向量(kx, ky)的长度为
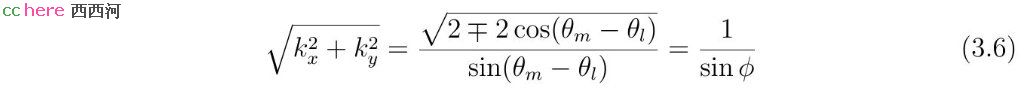
其中ϕ = (θm − θl)/2或者(θm − θl − π)/2,等于直线l与直线m之间夹角的一半。将式(3.5)代入方程组(3.1)的第一式,合并同类项后可以得到r需要满足的方程。
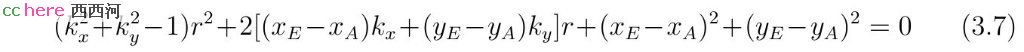
化简以后,可以得到式(3.7)的判别式为
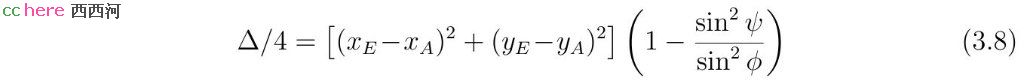
其中ψ为线段AE和角平分线a的夹角。直线l与直线m将整个平面分成四个区域。当ψ > ϕ,点A与角平分线a位于不同的区域,此时Δ < 0,r无实数解。当ψ = ϕ,点A位于直线l或直线m上,此时Δ = 0,r有一个实数解。当ψ < ϕ,点A与角平分线位于同一区域,此时Δ > 0,r有两个相异的实数解。得到r值以后,x和y值可以根据方程组(3.5)求出。
当l、m平行时,且点A在l、m之间,可以做与l、m等距的直线a来代替前述解法中的角平分线,采用完全相同的解法,将PLL问题转化为PPL问题和PPP问题求解。当l、m平行时,且点A在l、m外侧,问题无解。当l、m相交时,且点A不为l、m交点,那么依赖于A点的位置,可以将PLL问题转化为PPL问题和PPP问题求解。当l、m相交时,且点A为l、m交点,问题无解。
解的数目总结如下。
- 当直线l与直线m平行:a)A位于l、m之间:两个解;b)A位于l、m某条直线之上:一个解;c)A位于l、m外侧:无解;
- 当直线l与直线m相交:a)A不为l、m交点:两个解;b)l、m相交于A:无解。
令给定直线l、m分别经过点(xA, yA)、(xB, yB)且其法线与x轴正向夹角分别为θl、θm,给定圆圆心C的坐标为(xC, yC),半径为rC。假设所求圆圆心为(x, y),半径为r。那么LLC问题等价于求解如下非线性方程组。其中xA、yA、xB、yB、xC、yC、θl、θm、rC为已知量,x、y、r为未知量。
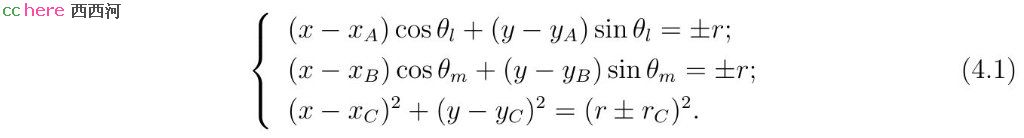
方程组(4.1)的第一式要求直线l与所求圆相切。第二式要求直线m与所求圆相切。第三式要求圆C与所求圆相切。由于一个点到一条直线的距离可以是正值也可以是负值,第一式和第二式的右侧可以取正号也可以取负号。类似,两圆可以内切也可以外切,第三式的两个半径可以相加也可以相减。
引入新变量r′ = r ± rC及坐标原点到直线l、m的法线长度pB、pC,方程组(4.1)等价于如下方程组。
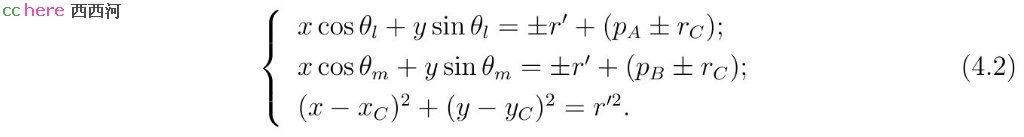
方程组(4.2)用于求解某圆,其圆心与LLC问题所求圆相同,但是半径不同。第一式表示该圆与某平行于l的直线相切,该直线与l的距离为rC。第二式表示该圆与某平行于m的直线相切,该直线与m的距离为rC。第三式表示该圆经过圆C圆心。这意味着LLC问题可以通过转换为PLL问题求解。
在平移l、m时,每条直线平移的方向有两个选择。依据圆A与l、m的相对位置,每个平移方向对应于与圆A外切或者内切。平移方向的选择应协调,使得所求圆与圆A外切或者内切。
首先考虑l、m相交的情况。四种平移方向的组合中,每种组合中l、m平移后将平面分成四个区域。当给定圆圆心在其中两个区域中时,有两解;当圆心在另两个区域中时,无解;当圆心在某条直线上时,有一解;当圆心为两直线交点时,无解。将四种情况相加,此时LLC问题可能有八解、六解或四解。类似地可以考虑l、m平行的情况,此时LLC问题可能有四解、三解、两解、一解或无解。

解的数目总结如下。
- 当直线l与直线m平行:a)圆A位于l、m之间,或者与l、m都相交:四个解;b)圆A与l、m中一条直线相切,并且位于l、m之间或与剩下一条直线相交:三个解;c)圆A与l、m中一条直线相交,或者圆A与l、m同时相切:两个解;d)圆A与l、m中一条直线相切,且位于l、m外侧:一个解;e)圆A位于l、m外侧:无解;
- 当直线l与直线m相交:a)圆A与l、m都相交:八个解;b)圆A与l、m中一条直线相切,且与剩下一条直线相交:六个解;a)其他情况:四个解。