- 近期网站停站换新具体说明
- 按以上说明时间,延期一周至网站时间26-27左右。具体实施前两天会在此提前通知具体实施时间
主题:阿波罗尼奥斯问题-Prob. of Apollonius -- 理性网民
问题:给定点A及两圆B、C,找出过A点且与圆B、C同时相切的圆(如图)。
解:过B、C两圆圆心做直线l,与两圆的公切线m交于O点。两圆与m分别相切于P、Q两点。过A、P、Q三点做圆D,与A、O两点的连线n相交于R点。则所求圆必过R点,可以采用PPC问题的解法。
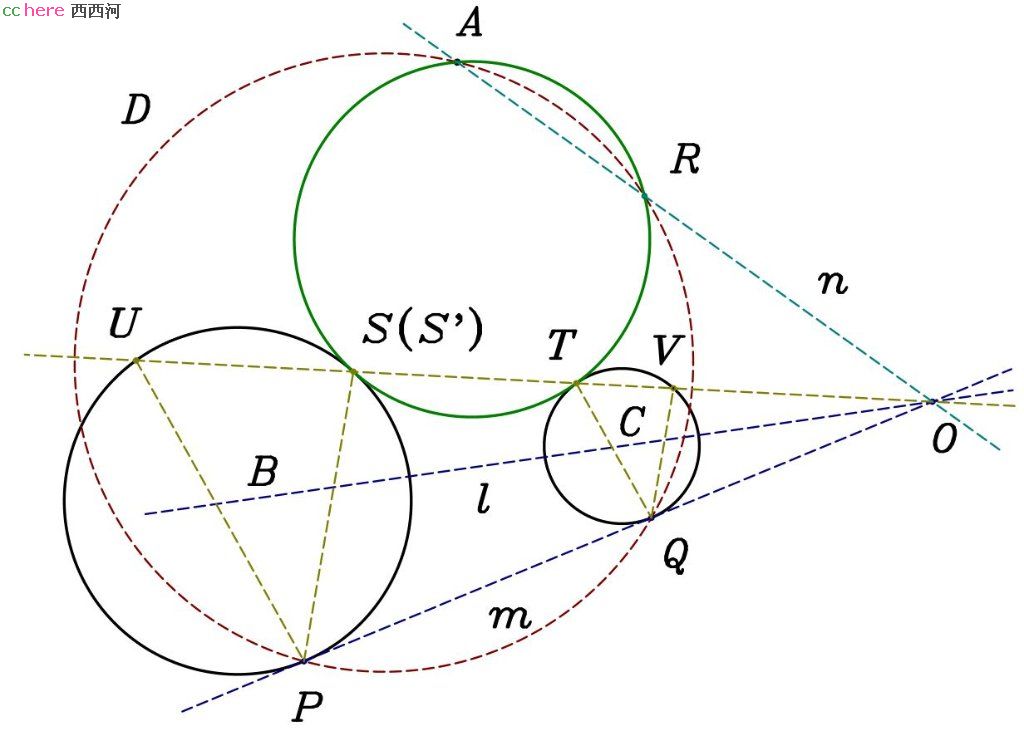
证明:令过A、R两点且与圆C相切的圆与圆C相切于T点。延长OT与圆B相交于S点,与所求圆相交于S′点。现在我们需要证明S与S′为同一点。由于A、R、T、S′四点共圆,|OS′|×|OT| = |OA|×|OR|。又A、R、P、Q四点共圆,|OA|×|OR| = |OP|×|OQ|。故|OS′|×|OT| = |OP|×|OQ|。令OT所在直线与圆B、圆C除S、T两点以外的交点为U、V两点。连接PS、PU及QT、QV。可以证明三角形OPS与三角形OQV相似,三角形OPU与三角形OQT相似,那么|OS|/|OV| = |OP|/|OQ|(等式1)且|OU|/|OT| = |OP|/|OQ|(等式2)。由于m与圆B、圆C分别相切于P、Q两点,|OP|2 = |OS|×|OU|(等式3)且|OQ|2 = |OT|×|OV|(等式4)。由等式1、2可以得到|OS|×|OT| = |OU|×|OV|,而由等式3、4可以得到|OP|2×|OQ|2 = |OS|×|OU|×|OT|×|OV|。综合此二式可以得到|OS|×|OT| = |OP|×|OQ|。与|OS′|×|OT| = |OP|×|OQ|相比较可得|OS′| = |OS|,故S与S′为同一点。这样我们证明了所求圆与圆B有一个交点。假设所求圆与圆B有另一个交点S″,那么连接OS″,可以采用类似的方法证明OS″所在直线经过圆C与所求圆的交点。这与圆C与所求圆相切矛盾。故所求圆与圆B相切与S点。
分析:通常情况下,给定两个圆B、C,可以在BC所在直线上找到两个点满足|OB|/|OC| = RB/RC。得到O点以后,我们可以根据已知点A找到点R并将问题转化为PPC问题求解。由于PPC问题最多有两个解,这意味着PCC问题最多有四个解。
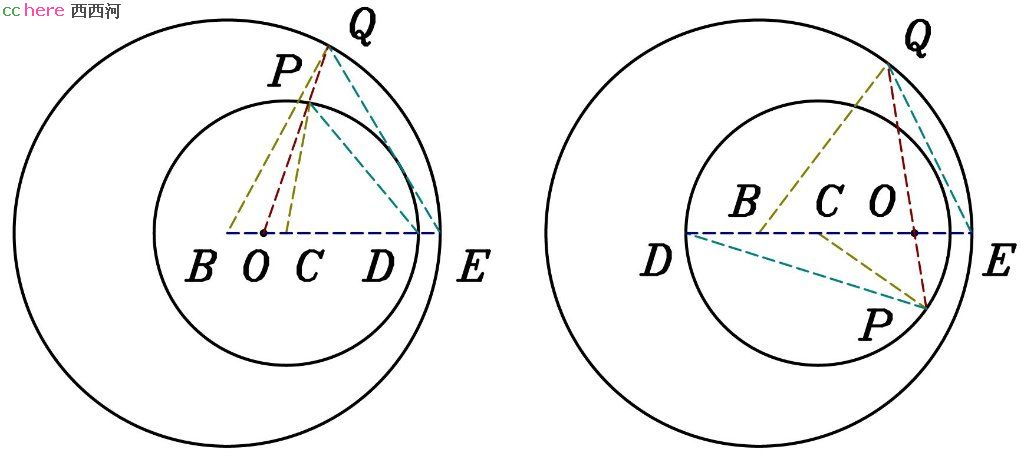
评论:点O在直线BC上,且满足|OB|/|OC| = RB/RC,其中RB和RC分别表示圆B和圆C的半径。如果采用O点作为反演中心,取k2 = (|OB|–RB)×(|OC|+RC) = (|OB|+RB)×(|OC|–RC)为变换常数,那么圆B与圆C在变换前后互换位置,所求圆在变换前后不变。当圆B与圆C外离时,O点可以由两圆的外切线或者内切线与直线BC相交得到。普遍情况下,O点位置可通过将线段BC成比例划分得到。图中以两圆内含的情况为例子,说明以O点为中心的反演变换确实将圆B圆C位置互换。延长BC与两圆分别交于D、E两点,过O点做直线分别与两圆交于P、Q两点。连接BQ、CP、DP、EQ。那么|BQ|即为圆B的半径,|CP|即为圆C的半径。由|OB|/|OC| = RB/RC = |BQ|/|CP|可以得到|OB|/|BQ| = |OC|/|CP|。因为∠BOQ与∠COP互补,所以∠BQO = ∠CPO,也就是说∠OEQ–∠OQE = ∠OPD–∠ODP。因此三角形ODP与三角形OEQ相似。那么|OP|×|OQ| = |OD|×|OE|。这意味着如果我们选取点O为变换中心且|OD|×|OE|为变换常数,圆B与圆C的位置互换。
- 相关回复 上下关系8
🙂【8】PLC问题 2 理性网民 字1831 2020-08-07 11:11:48
🙂【7】CCC问题 2 理性网民 字1333 2020-08-02 18:19:30
🙂【7.1】解析几何方法 7 理性网民 字1092 2021-02-11 00:35:15
🙂【6】PCC问题

🙂【6.1】解析几何方法 理性网民 字2920 2021-02-07 13:13:58
🙂【补充】基于向量的公式推导 1 理性网民 字1702 2021-02-07 13:18:58
🙂【5】PPC问题 2 理性网民 字2007 2020-07-28 12:12:54
🙂【5.2】解的存在性和个数 1 理性网民 字960 2020-11-09 10:05:39